Картинка в системе координат: Рисуем по координатам. Рисунки и фигуры

Координатная плоскость картинка — 82 фото

Координатная плоскость с координатами для 6 класса

Рисунки на плоскости с координатами

Рисунок по точкам на координатной плоскости с координатами

Координатная плоскость с координатами

Координатная плоскость 20 точек

Фигуры на координатной плоскости с координатами 6 класс

Рисование на координатной плоскости

Рисунки с координатами

Птица на координатной плоскости с координатами

Рисунок по координатам (-2;2),(-2;-4)

Рисунки на координатной плоскости

Сердце на координатной плоскости

Координатный рисунок с координатами

Рисунок в системе координат по точкам

Рисование по координатам

Координатная плоскость для печати а4

Рисунки по координатам с координатами

Рисунок на плоскости

Координатная плоскость для построения графиков

Лист в клеточку с осями координат

Координатная плоскость с координатами пустая

Координатная плоскость (-4;6),(-3;5)

Рисунки на координатной плоскости

Координатные плоскости (-1,-7),(-5,-3),(-5,-3)

Воробей по координатам

Кленовый лист на координатной плоскости

Рисунки на координатной плоскости

Координатная плоскость (-4;6),(-3;5)

Координатная плоскость -3п и -2п

Петух по координатам

Координатные плоскости (-1,-7),(-5,-3),(-5,-3)

Координатная сетка для рисования

Лист в клеточку с системой координат

Координатная сетка

Координатная плоскость для печати

Слоник на координатной плоскости 2 -3

Координатная плоскость пустая

Координатная плоскость система координат

Квадранты координатной плоскости

Оси координат сантиметры

Координата я плоскость

Акула на координатной плоскости

Система координат сетка

Рисование по координатной

Сантиметровая сетка а4

Бабочка в кумире чертежник

Координатная сетка пустая

Координаты рисунки по точкам

Оси координат в клетку

Рисунки на координатной плоскости сложные

График функции пустой

Координатная плоскость пустая

Пикачу по координатам с координатами

Корабль по координатам

Система координат с пи

X Y координаты

Верблюд на координатной плоскости -10 -2

Декартовая система координат на плоскости

Лебедь на координатной плоскости с координатами

Координатная сетка

Конь на координатной плоскости

Отметьте на координатной плоскости точки а3,6

Координаты бабочки

Декартова система координат в авиации

Координатная плоскость фон

Самолет по координатам

Координатная плоскость с пи

Система координат на прозрачном фоне

Оси координат х и у

Зайчонок на координатной плоскости 5. 1

Собака на координатной плоскости 14;-3

Мышка на координатной плоскости

Координатная сетка для графиков

Симметричные рисунки

Координатная ось система координат

Рисунки по координатам сложные

Лиса на координатной плоскости

Координатная плоскость пустая

Ось координат

Координатная плоскость картинка

Координатная прямая картинка — 70 фото

Координатная плоскость с координатами

Координатная плоскость 20 точек

Рисунки на координатной прямой

Сетка для построения графиков

Декартова система координат на плоскости рисунки

Рисование на координатной плоскости

Координатные плоскости (-1,-7),(-5,-3),(-5,-3)

Рисунок 50 координатных точек

Рисунок на координатной плоскости с координатами

Декартова система координат в авиации

Координатные прямые животные

Ось х и у график

Пони на координатной плоскости

Изображение координатной оси

Координатная ось

Фигуры по точкам в системе координат

Система координат x y

Координаты шаблон

Рисунки на координатной плоскости

Система координат для построения Графика

Система координат на плоскости шаблон

Рисунки на координатной плоскости

Слоник на координатной плоскости -1 4

Рисунок на плоскости

Верблюд по точкам на координатной

Бабочка на координатной плоскости

Система координатных сеток

Координатная прямая на клетчатой бумаге

Ось Икс ось Игрек

Оси координат х и у

Координатная прямая с точками

Координатная прямая рисунок

Система координат сетка

Петушок по координатам

Звезда на координатной плоскости

Бабочка по координатам

Координатная сетка а4

Координатная ось 6 класс задания

Координатный числовой Луч

Координатная прямая на клеточной бумаге

Модуль на координатной прямой

Координатная ось с единичным отрезком

Интервал полуинтервал отрезок Луч таблица

Фигуры из отрезков

Положительные и отрицательные числа на координатной прямой 6 класс

Сердце на координатной плоскости

Тригонометрическая ось координат

Система координат на плоскости

Координатные плоскости (-1,-7),(-5,-3),(-5,-3)

Рисунок на координатной плоскости с координатами

Координатная прямая с единичным отрезком 10 клеток

Координатная плоскость для тригонометрических функций

Собака на координатной плоскости 14;-3

Координаты противоположных колениарнхвекторов

Числовая прямая с отрицательными и положительными числами

Координатная прямая и координатная ось

Система координат на плоскости

Координатная плоскость система координат

Координатное рисование

1.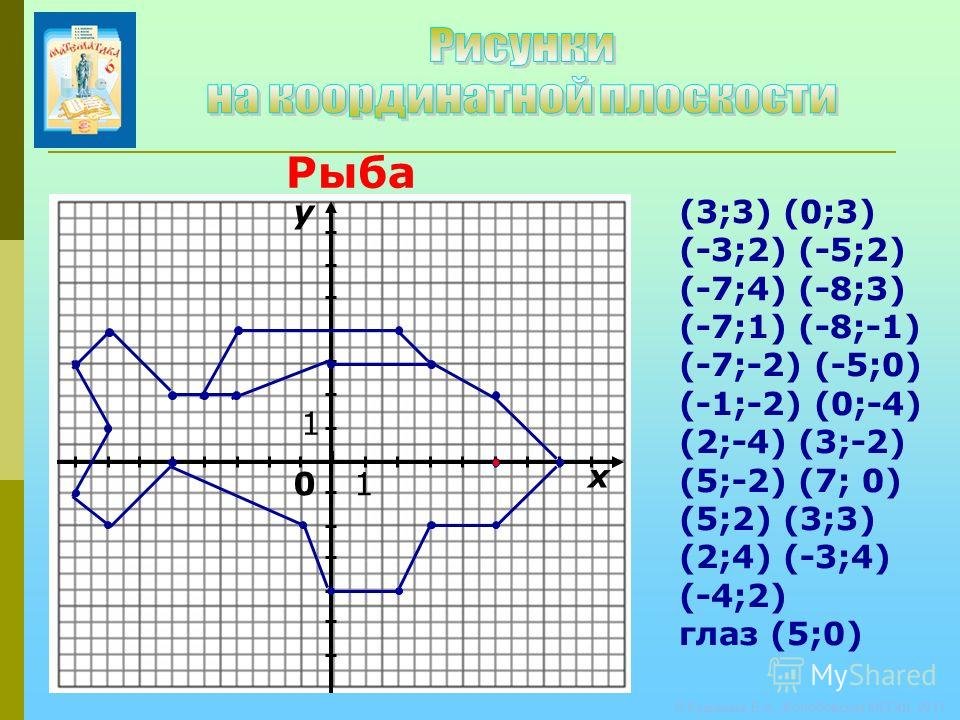 5 На координатной плоскости

Запиши координаты точек a b c d e f m

Система координат на плоскости

Координатные плоскости (-1,-7),(-5,-3),(-5,-3)

X Y координатная система

Полярная координатная плоскость

Рисование собаки по координатам

На координатной прямой отмечено число а

Рисунки с координатами

систем координат изображения
— MATLAB & Simulink

Системы координат изображения

Вы можете получить доступ к местоположениям на изображениях, используя несколько различных систем координат изображения.
Вы можете указывать местоположения, используя дискретные пиксельные индексы, потому что изображения хранятся как
массивы. Вы также можете указать местоположения, используя непрерывные пространственные координаты, потому что
изображения представляют сцены реального мира в непрерывном пространстве.

Индексы пикселей

Как описано в изображениях в MATLAB, MATLAB ^® хранит большинство изображений в виде массивов. Каждый (строка, столбец) индекс массива
соответствует одному пикселю отображаемого изображения.

Существует однозначное соответствие между индексами пикселей и нижними индексами для
первые два измерения матрицы. Подобно индексации массива в MATLAB, индексы пикселей являются целыми значениями и находятся в диапазоне от 1 до длины
строку или столбец. Индексы располагаются сверху вниз и слева направо.
верно.

Например, данные для пикселя в пятой строке, второй столбец хранятся в
матричный элемент (5,2). Вы используете обычную индексацию матрицы MATLAB для доступа к значениям отдельных пикселей. Для
например, код MATLAB

 I(2,15) 

возвращает значение пикселя в строке 2 столбца 15 одноканального изображения.
я . Точно так же код MATLAB

 RGB(2,15,:) 

возвращает значения цвета пикселя в строке 2, столбце 15 многоканального
изображение РГБ .

Пространственные координаты

В системе пространственных координат местоположения на изображении
положения на непрерывной плоскости. Места описываются в терминах декартовой
x и y координаты (не строки и столбца
индексы, как в системе индексации пикселей). С этой картезианской точки зрения
( x , y ) расположение, такое как (3.2, 5.3)
осмысленной и отличной от координаты (5, 3).

Image Processing Toolbox™ определяет два типа пространственных систем координат в зависимости от кадра
ссылки. Внутренние координаты задают местоположения по отношению к изображению.
точка зрения. Мировые координаты определяют местоположение по отношению к внешнему
мировой наблюдатель.

Внутренние координаты

По умолчанию набор инструментов определяет пространственные координаты изображения с помощью
внутренняя система координат . Эта пространственная координата
система соответствует индексам пикселей изображения. Внутренние координаты
( x , y ) центральной точки любого
пикселя идентичны индексам столбца и строки для этого пикселя. Например,
центральная точка пикселя в строке 5 столбца 3 имеет пространственные координаты
х = 3,0, у = 5,0. Имейте в виду,
однако порядок внутренних координат (3.0, 5.0) обратный относительно
индексам пикселей (5,3).

Внутренние координаты центра каждого пикселя имеют целочисленное значение.
центр верхнего левого пикселя имеет внутренние координаты (1.0, 1.0). Центр
нижнего правого пикселя имеет внутренние координаты ( numCols ,
numRows ), где numCols и
numRows — количество строк и столбцов в изображении.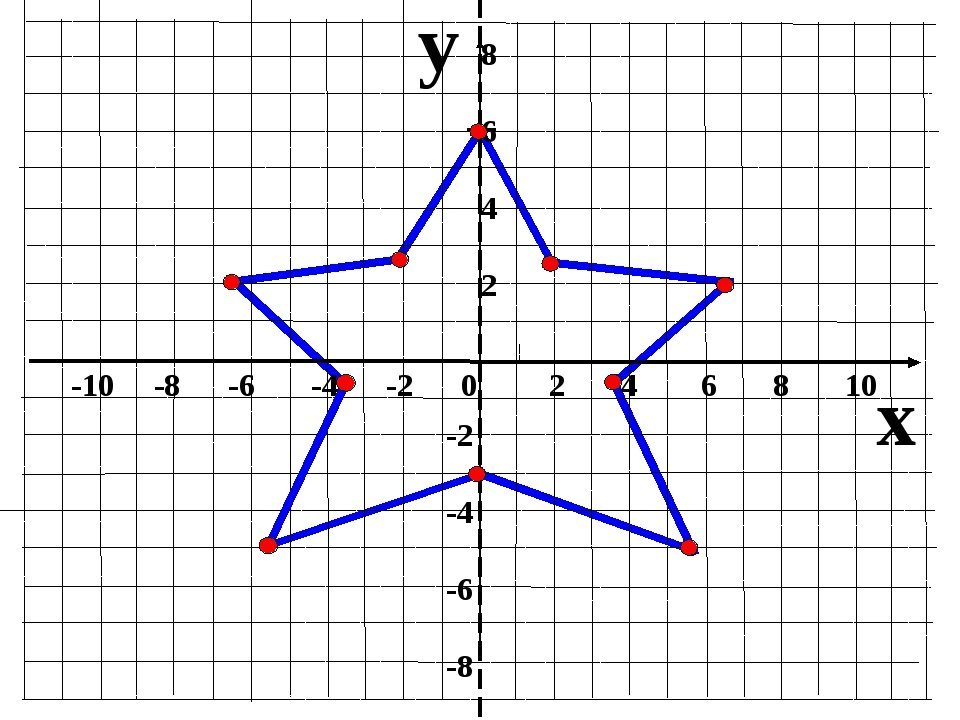
Как правило, центр пикселя с индексами пикселей ( м ,
n ) попадает в точку х =
n , y = м в
внутреннюю систему координат.

Поскольку размер каждого пикселя во внутренней системе координат составляет одну единицу,
границы изображения имеют дробные координаты. Верхний левый угол
изображения находится в точке (0,5, 0,5), а не в точке (0, 0). Аналогично, правый нижний
угол изображения находится в точке ( numCols + 0,5,
numRows + 0,5).

Некоторые функции в основном работают с пространственными координатами, а не с пикселями
индексы, но пока вы используете систему пространственных координат по умолчанию
(внутренние координаты), вы можете указать местоположения с точки зрения их столбцов
( x ) и строки ( y ).

Мировые координаты

A мировая система координат (также называется нестандартным
пространственная система координат) ослабляет некоторые ограничения внутренней
система координат. В мировой системе координат пиксели могут иметь любую длину и
ширину, и они могут быть центрированы по любой координате.

Некоторые ситуации, когда вы можете захотеть использовать мировую систему координат, включают:

• При выполнении геометрического преобразования, такого как перемещение,
  на изображении и хотите сохранить информацию о том, как новый
  положение относится к исходному положению.

• Когда пиксели не квадратные. Например, в магнитном резонансе
  изображений (МРТ), вы можете собирать данные таким образом, чтобы пиксели имели более высокое
  частота дискретизации в одном направлении, чем в ортогональном направлении.

• Когда вы знаете, как экстент пикселей выравнивается с позициями в
  реальный мир. Например, на аэрофотоснимке каждый пиксель
  может покрывать определенный участок земли размером 5 на 5 метров.

• Если вы хотите изменить направление
  x — ось или y — ось. Это
  общий метод для использования с геопространственными данными.

Существует несколько способов определения мировой системы координат. Вы можете использовать
объекты пространственной привязки, которые кодируют местоположение изображения в мире
систему координат, разрешение изображения и то, как экстент изображения связан с
внутренние и мировые координаты. Вы также можете указать максимальное и минимальное
координаты в каждом измерении. Дополнительные сведения см. в разделе Определение мировой системы координат изображения.

Связанные примеры

• Сдвиг диапазона X- и Y-координат отображаемого изображения

Подробнее о

• Изображения в MATLAB
• Определить мировую систему координат изображения

Отображение изображений в системе координат изображения — ArcMap

• Системы координат изображения
• Предварительный просмотр элемента набора данных мозаики

Система координат изображения (ICS) отображает ваши изображения без искажений. Он может это сделать, потому что система координат фрейма данных такая же, как та, в которой были захвачены ваши изображения. Так как изображения в системе координат изображения не искажены, он идеально подходит для использования с наклонными изображениями и измерениями. Системы координат изображения поддерживаются в ArcMap и REST API сервисов изображений ArcGIS Server.

Координаты изображения доступны на изображениях, которые содержат информацию о преобразовании сенсора, такую ​​как коэффициенты рационального полинома (RPC) или кадровые камеры. Система координат изображения состоит из домена (собственного экстента), преобразований геоданных и информации о пространственной привязке карты из соответствующего изображения.

Системы координат изображения

Как правило, ваш фрейм данных использует систему координат карты. Это означает, что пиксели вашего изображения преобразуются в координаты карты с использованием сенсорных моделей и проекций. Преобразование ваших изображений в координаты карты может привести к тому, что ваши изображения будут выглядеть перекошенными или искаженными.
из-за различных используемых преобразований и поправок на рельеф, особенно для наклонных изображений.

При использовании системы координат изображения можно настроить фрейм данных на использование системы координат одного изображения для установления координат.
система для фрейма картографических данных. Это изображение отображается неискаженным в исходном виде без необходимости различных преобразований и проекций.
Все
другие изображения, функции, ярлыки,
и аннотации проецируются для наложения этого изображения в его координатах изображения.
Система.

Для работы с системами координат изображения в ArcMap используйте окно Анализ изображения.

1. в
   В окне Анализ изображения выделите растровое изображение, на основе которого будет создана система координат изображения.
2. Щелкните слой правой кнопкой мыши и выберите «Фокус на изображении».

   Если изображение, которое вы щелкнули, не имеет связанной с ним системы координат изображения, параметр «Фокус на изображении» недоступен.

Координата кадра данных будет установлена ​​с координатой выбранного изображения. Изображение и слои на карте будут отображаться в одних и тех же координатах.

Примечание:

Чтобы вернуть фрейм данных обратно к координатам карты, щелкните Фокус на изображении/Фокус на сервисе изображений, чтобы снять флажок.

Система координат изображения может быть выбрана только для одного изображения в кадре данных. Это означает, что только одно изображение в наборе данных мозаики может использоваться для установки системы координат. Ниже приведены шаги по установке системы координат изображения для изображения в наборе данных мозаики.

1. Сделайте выбор в наборе данных мозаики.
2. В оглавлении щелкните правой кнопкой мыши подслой Footprint и выберите «Добавить выбранные растры на карту».

Теперь каждый отдельный растровый слой можно установить в качестве изображения фокуса.

Предварительный просмотр элемента набора данных мозаики

Каждый элемент набора данных мозаики имеет собственное окно свойств.

В этом окне свойств вы можете предварительно просмотреть элемент набора данных мозаики в системе координат карты или системе координат ICS. Вы также можете переключаться между видом «Север вверху» и видом «Сверху вверх» изображения.

Чтобы получить доступ к свойствам элемента набора данных мозаики, выполните следующие действия.

1. В оглавлении щелкните правой кнопкой мыши таблицу Footprint и выберите «Открыть таблицу атрибутов».
2. В таблице атрибутов щелкните поле Растр для элемента набора данных мозаики, который вы хотите просмотреть.