Картинка в системе координат: Рисуем по координатам. Рисунки и фигуры

Показ изображений в собственной системе координат—Справка

• Системы координат изображения
• Просмотр элемента набора данных мозаики

Система координат изображения (СКИ) показывает изображение без искажений. Это происходит, поскольку система координат фрейма данных та же, что и при съемке. Поскольку искажений нет, эта система координат идеально подходит для работы с перспективными снимками и измерений. СКИ поддерживаются в ArcMap и сервисах изображений ArcGIS Server REST API.

Координаты изображений доступны для изображений, у которых есть информация сенсора о трансформировании, например, коэффициенты рационального многочлена, или кадровых камер. Система координат изображений состоит из домена (исходный экстент), преобразований геоданных и информации о пространственной привязке карты, полученной из соответствующего изображения.

Системы координат изображения

Как правило, для Фрейма данных задана система координат карты. Это значит, что пиксели изображения будут трансформированы в координаты карты с учетом моделей сенсора и проекций. Конвертация изображения в координаты карты может привести к тому, что изображения будут выглядеть неестественно и искаженно из-за многочисленных примененных преобразований и коррекции за рельеф (особенно это касается перспективных изображений).

При использовании системы координат изображения вы можете задать Фрейм данных, чтобы использовать именно ее для карты. Это изображение будет показано без искажений в исходном экстенте, поэтому нет необходимости в проецировании и преобразованиях. Все другие изображения, объекты, надписи и аннотации проецируются для наложения с изображением в рамках его системы координат.

Для работы с СКИ в ArcMap используйте окно Анализ изображений.

1. 
   В окне Анализ изображений выберите изображение, на котором основывается СКИ.
2. Щелкните правой кнопкой слой и выберите Фокус на изображение (Focus on Image).

   Если у выбранного изображения система координат не задана, опция Фокус на изображении будет недоступна.

Координаты фрейма данных будут обновлены с учетом СКИ выбранного изображения. Изображение и слои на карте будут показаны в одной системе координат..

Примечание:

Чтобы вернуть Фрейму данных координаты карты, щелкните Фокус на изображение/Фокус на сервис изображений, чтобы снять отметку.

СКИ может быть выбрана только для одного изображения в Фрейме данных. Это значит, что только одно изображение в наборе данных мозаики может использоваться в качестве источника системы координат. Ниже приведены шаги по установке СКИ для изображения в наборе данных мозаики.

1. Выберите объект в наборе данных мозаики.
2. В таблице содержания щелкните правой кнопкой мыши на слое Контур и выберите Добавить выбранные растры на карту (Add Selected Rasters to Map).

Теперь каждый отдельный слой растра может быть указан в качестве фокусного изображения.

Просмотр элемента набора данных мозаики

У каждого элемента в наборе данных мозаики есть свое окно свойств.

В этом окне вы можете просмотреть элемент в системе координат Карты или СКИ. Вы также можете переключиться между видом изображения Север вверху (North Up) и видом Вверх (Top Up).

Чтобы получить доступ к свойствам элемента набора данных мозаики, выполните следующее.

1. В таблице содержания щелкните правой кнопкой мыши на таблице контуров и щелкните Открыть таблицу атрибутов (Open Attribute Table).
2. В таблице атрибутов щелкните поле Raster для элемента, который хотите просмотреть.

   Появится небольшая стрелка.

3. Нажмите на нее.

   Откроется окно свойств элемента набора данных мозаики.

4. Откройте закладку Просмотр.

Вы можете выбрать, в какой системе координат вы хотите его просмотреть.

Связанные темы

Отзыв по этому разделу?

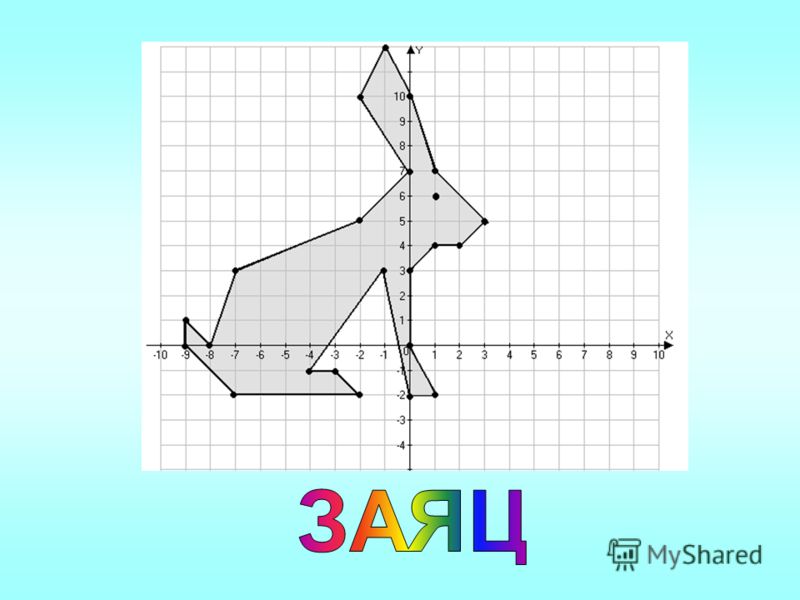
РИСУНКИ ПО КООРДИНАТАМ

Точками координат рисунок.

Учителя, постоянно в поиске: как, не меняя содержание материала, найти способы овладения им и его применения, как заинтересовать учащихся в изучении данной темы, как сформировать у них прочные знания.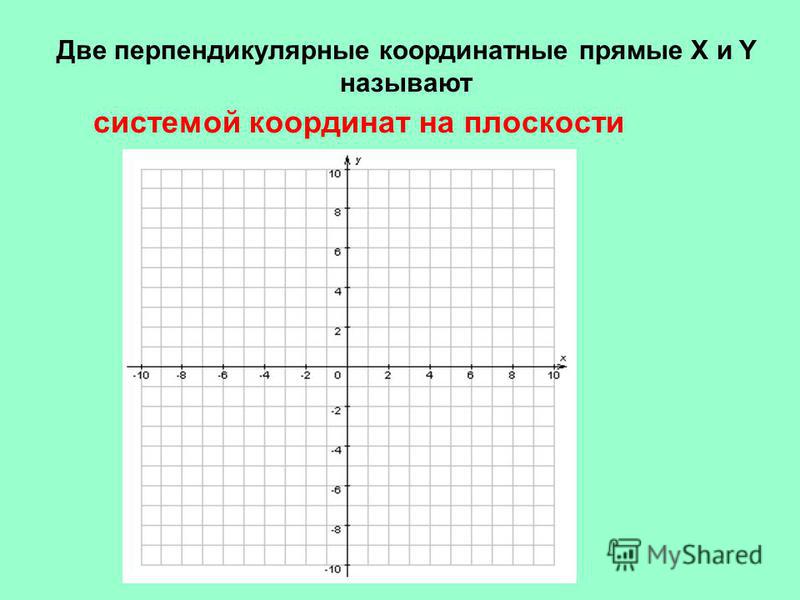 При изучении темы «Координатная плоскость» можно подойти творчески, по данным координатам точек можно нарисовать знакомую картинку. Такие задания увлекают детей, заинтересовывают, и многие сами затем с удовольствием составляют рисунки по координатам. Эта творческая работа носит и воспитательный характер.

Для вас, были составлены данные задания, а некоторые из них взяты из еженедельной учебно-методической газеты «Математика». На координатной плоскости отмечаем точки, заданные своими координатами, в порядке их следования. А затем соединяем каждую точку с предыдущей кривой или отрезком. Что в результате получится, вы увидите в итоге.

Этот сборник заданий поможет любому учителю организовать творческий подход к изучению данной темы и получить хорошие результаты в её усвоении.

Правила игры.

Вариант 1

1.Распечатайте карточки. Обрадуйте ребенка, что будет новая интересная игра. Скажите ему, что игра называется — Рисунки по координатам.

2.Объясните ребёнку принцип нахождения адреса клетки на пересечении столбца с цифрой и строчки с буквой.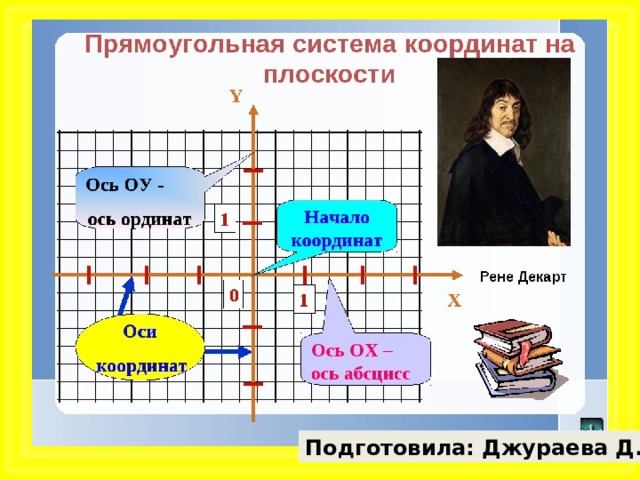

3.Предложите ребёнку закрасить клетки, указанные в таблице под игровым полем.

4.Нашли клетку по её адресу, зачеркнули адрес. Это необходимо, чтобы ребёнок не запутался, какую клетку он уже нашёл.

5.Посмотрите на игровое поле, пусть ребёнок назовёт предмет, который у него получился в результате выполнения задания.

Вариант 2

Объясняете тоже самое, а именно, как играть, как считать, на что опираться- только объясните теперь, что диктуете вы.

Удачи Вам!

Ваша Ментальная Арифметика.

Ласточка

(-5; 4), (-7; 4), (-9; 6), (-11; 6), (-12; 5), (-14; 5), (-12; 4), (-14; 3), (-12; 3), (-11; 2), (-10; 2),

(-9; 1), (-9; 0), (-8; —2), (0; —3), (3; —2), (19; —2), (4; 0), (19; 4), (4; 2), (2; 3), (6; 9), (10; 11), (3; 11), (1; 10), (-5; 4), глаз (-10,5; 4,5).

Утка

(3; 0), (1; 2), (-1; 2), (3; 5), (1; 8), (-3; 7), (-5; 8), (-3; 4), (-6; 3), (-3; 3), (-5; 2),(-5; —2), (-2; —3), (-4; —4), (1; —4), (3; —3), (6; 1), (3; 0) и (-1; 5).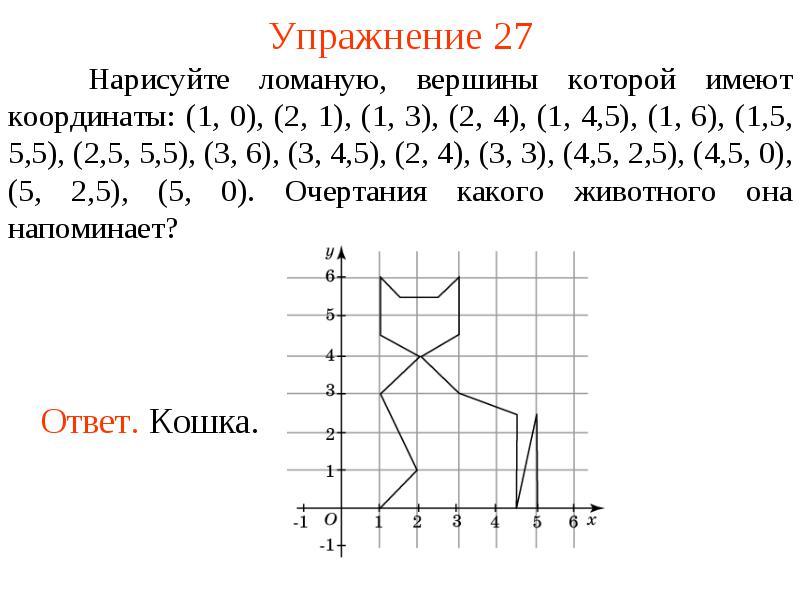

Слоник 1

(-1; 4), (-2; 1), (-3; 2), (-4; 2), (-4; 3), (-6; 4), (-6; 6), (-8; 9), (-7; 10), (-6; 10), (-6; 11), (-5; 10), (-4; 10), (-3; 9), (-1; 9,5), (1; 9), (3; 10), (4; 11), (4; 16), (3; 18), (5; 17), (6; 17), (5; 16), (6; 12), (6; 9), (4; 7), (1; 6),

(2; 5), (5; 4), (5; 3), (4; 4), (1; 2), (1; 0), (3; —4), (4; —5), (1;-7), (1; —6), (0; —4), (-2; —7), (-1,5; —8), (-5; —7), (-4; —6), (-5; —4), (-7;-5), (-7; —7), (-6,5; —8), (-10,5; —8), (-10; —7), (-10; —6), (-11; —7),

(-11; —8), (-14; —6), (-13; —5), (-12; —3), (-13; —2), (-14; —3), (-12; 1), (-10; 3), (-8; 3), (-6; 4), глаз (-1; 7).

Верблюд

(-10; —2), (-11; —3), (-10,5; —5), (-11; —7), (-12; —10), (-11; —13), (-13; —13), (-13,5; —7,5), (-13; —7), (-12,5; —5), (-13; —3), (-14; —1), (-14; 4), (-15; —6), (-15; —3), (-14; 2), (-11; 4), (-10; 8), (-8; 9),

(-6; 8), (-5; 5), (-3;8),(-1;9), (0;8), (0,5;6), (0,5;4), (3;2,5), (4;3), (5;4), (6;6), (8;7), (9,5;7), (10;6), (11,5;5,5), (12;5), (12;4,5), (11;5), (12;4), (11;4), (10;3,5), (10,5;1,5), (10;0), (6;-3),

(2;-5), (1,5;-7), (1,5;-11), (2,5;-13), (1;-13), (0;-5), (-0,5;-11), (0;-13), (-1,5;-13), (-1,5;-7),

(-2;-5), (-3;-4), (-5;-4,5), (-7;4,5), (-9;-5), (-10;-6), (-9;-12), (-8,5;-13), (-10,5;-13), (-10;-9,5), (-11;-7), глаз (8,5;5,5)

Медведь 1

(4;-4), (4;-6), (8,5;-7,5), (9;-7), (9;-6), (9,5;-5), (9,5;-3,5), (10;-3), (9,5;-2,5), (4;5), (3;6), (2;6), (0;5),(-3;5), (-7;3), (-9;-1), (-8;-5), (-8;-7), (-4,5;-8), (-4,5;-7), (-5;-6,5), (-5;-6), (-4,5;-5), (-4;-5), (-4;-7), (-1;-7),(-1;-6), (-2;-6), (-1;-4), (1;-8), (3;-8), (3;-7), (2;-7), (2;-6), (3;-5), (3;-6), (5;-7),

(7;-7), ухо (6;-4), (6;-3), (7;-2,5), (7,5;-3), глаз (8;-6)

Лось

(-2;2), (-2;-4), (-3;-7), (-1;-7), (1;4), (2;3), (5;3), (7;5), (8;3), (8;-3), (6;-7), (8;-7), (10;-2), (10;1), (11;2,5),(11;0), (12;-2), (9;-7), (11;-7), (14;-2), (13;0), (13;5), (14;6), (11;11), (6;12), (3;12), (1;13), (-3;13), (-4;15),(-5;13), (-7;15), (-8;13), (-10;14), (-9;11), (-12;10), (-13;9), (-12;8),

(-11;9), (-12;8), (-11;8), (-10;7), (-9;8),(-8;7), (-7;8), (-7;7), (-6;7), (-4;5), (-4;-4), (-6;-7), (-4;-7), (-2;-4), глаз (-7;11)

Зайчонок

(5;1), (6;2), (6;3), (5;6), (4;7), (5;8), (6;8), (8;9), (9;9), (7;8), (9;8), (6;7), (7;6), (9;6), (11;5), (12;3), (12;2), (13;3), (12;1), (7;1), (8;2), (9;2), (8;3), (6;1), (5;1) и (5;7).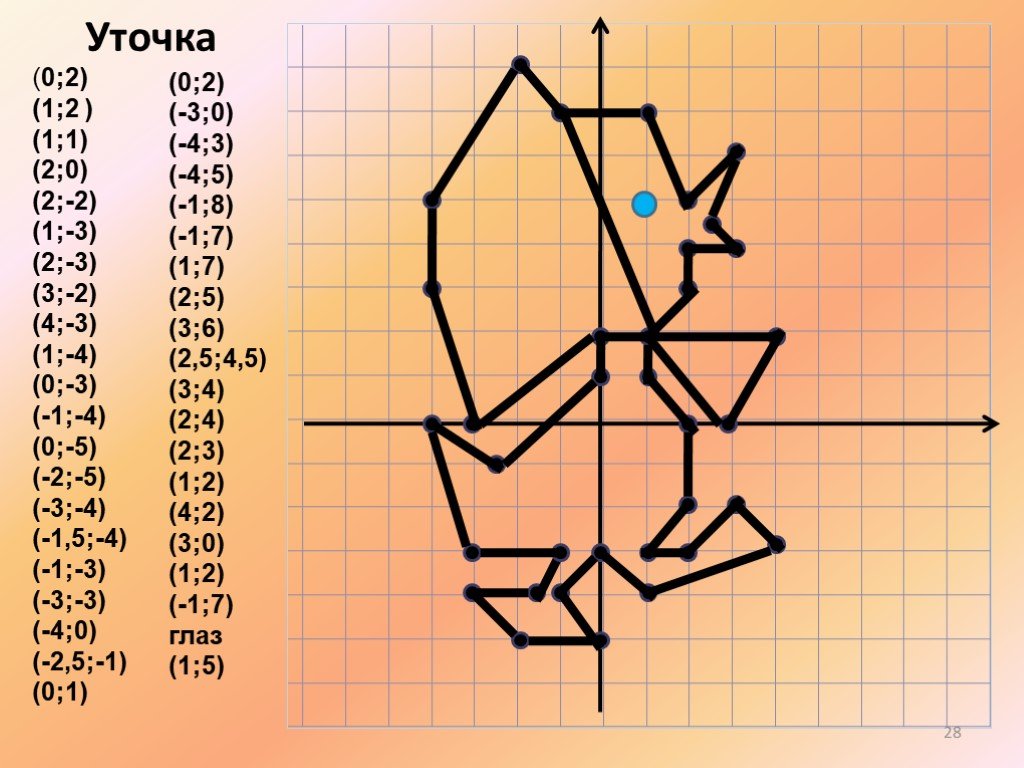

Лиса 1

(0,5;0), (1;2), (1;3), (2;4), (3;3,5), (3,5;4), (2,5;5), (2,5;6), (2;6,5), (2;8,5), (1;7), (0,5;6,5),

(-0,5;7), (-0,5;6), (-1;5,5), (-3;3), (-4;1), (-4,5;-1,5), (-4;-2,5), (-4,5;-3,5), (-3,5;-5), (-1;-6), (1;-7), (2;-8), (3,5;-10), (4,5;-9),(4,5;-7), (4;-6), (3;-5), (0;-4,5), (1;-1,5), (0,5;0).

Собака 1.

(1;-3), (2;-3), (3;-2), (3;3), (4;3), (5;4), (5;6), (4;7), (3;7), (2;6), (3;5), (3;5,5), (4;5), (3;4), (2;5), (-3;5),

(-4;6), (-4;9), (-5;10), (-5;11), (-6;10), (-7;10), (-7;10), (-7;8), (-9;8), (-9;7), (-8;6), (-6;6), (-7;3), (-6;2), (-6;-1), ў(-7;-2), (-7;-3), (-6;-3), (-4;-2), (-4;2), (1;2), (2;-1), (1;-2), (1;-3)

Лиса 2

(7,5;5), (-4;7), (-3;7), (-3;9), (1;1), (3;0), (5;-0,5), (7;-4), (7;-8), (10;-5), (13;-3), (17;-2), (19;-2), (17;-3), (14;-7), (7;-9), (6;-10), (2;-10), (2;-9), (5;-9), (3;-8), (1,5;-6), (0,5;-3),(0,5;-10),(-2,5;10), (-2,5;-9), (-1;-9), (-1;-3), (-3;-10), (-6;-10), (-6;-9), (-4,5;-9), (-3;-4), (-3;0,5), (-4;3), (-5;3),

(-7,5;4), (-7,5;5)

Собака 2.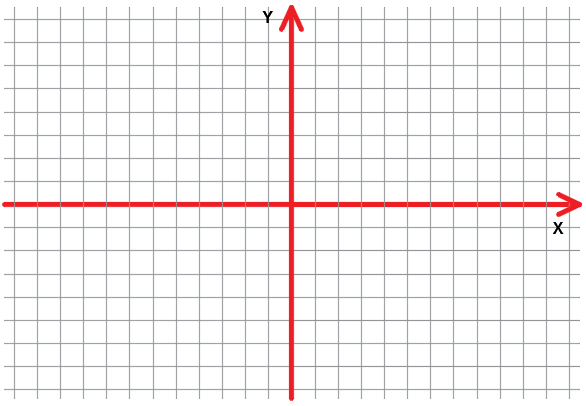

а) (14;-3), (12;-3), (8,5;-2), (4;3), (2;4), (1;5), (1;8), (-2;5), (-3;5), (-6;3), (-7;1), (-11;-1), (-10;-3), (-6;-4), (-2;-4), (-1;-3), (1;-5), (1;-8), (-2;-10), (-11;-10), (-13;-11), (-13;-13), (4;-13), (5;-12),

(9;-12)

б) (14;-10), (10;-10), (9;-11), (9;-13), (14;-13)

Медведь 2

(-18;4), (-18;3), (-17;3), (-18;2), (-17;2), (-11;1), (-9;0), (-8;-1), (-11;-6), (-12;-8), (-14;-10),

(-10;-10), (-8;-6), (-5;-4), (-4;-7), (-4;-8), (-6;-10), (-1;-10), (-1;-2), (1;-4), (5;-4), (5;-8), (3;-10), (8;-10), (10;-4), (12;-6), (10;-8), (15;-8), (14;-2), (15;2), (14;6), (12;8), (8,9), (4;9), (0;8), (-6;9), (-11;7), (-15;6), (-18;4)

Воробей

(-6;1), (-5;-2), (-9;-7), (-9;-8), (-5;-8), (-1;-5), (3;-4), (5;-1), (8;1), (9;3), (2;2), (4;6), (3;11), (2;11), (-2;6), (-2;2), (-4;4), (-5;4), (-6;3), (-6;2), (-7;2), (-6;1)

Ёжик

(2;-1), (3,5;0,5), (4;-1), (5;0), (4;2), (2;1), (2;3), (4;5), (4;6), (2;5), (1;7), (1;8), (0;7), (0;9), (-1;7), (-2;8),(-2;7), (-3;7), (-2;6), (-4;6), (-3;5), (-4;5), (-3;4), (-5;4), (-4;3), (-5;3), (-4;2), (-6;2), (-5;1), (-6;1), (-5;0),(-6;0), (-5;-1), (-6;-2), (-4;-2), (-5;-3), (-3;-4), (-4;-5), (-2;-5), (-1;-6), (3;-6), (3;-5), (1;-5), (1;-4), (2;-3), (2;-1)

Заяц

(-14;2), (-12;4), (-10;5), (-8;10), (-7;11), (-8;5), (-7;4), (-5;1), (-3;1,5), (3;0), (8;1), (10;0), (11;2), (12;1), (12;0), (11,5;-1), (13;-5), (14;-4,5), (15;-9), (15;-11), (13,5;-6,5), (11;-8), (8;-5), (-1;-7),

(-5;-6), (-7;-7), (-9;-7), (-11;-6,5), (-13;-7), (-15;-6), (-12;-5,5), (-9;-6), (-11;-1), (-13;0), (-14;2).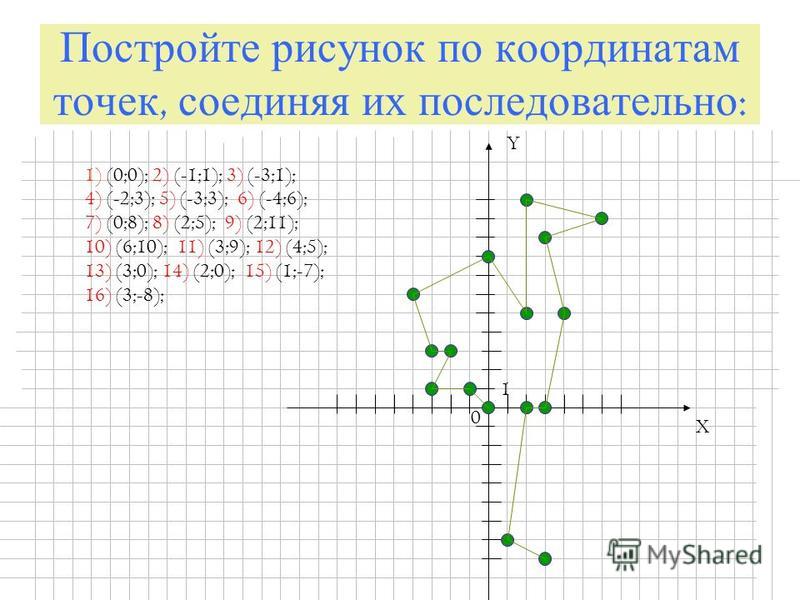

Голубь

(-4;8), (-5;7), (-5;6), (-6;5), (-5;5), (-5;4), (-7;0), (-5;-5), (-1;-7), (3;-7), (9;-2), (13;-2), (14;-1), (6;1),(8;4), (15;7), (3;8), (2;7), (0;3), (-1;3), (-2;4), (-1;6), (-2;8), (-4;8)

Снегирь

(5;-2), (0;3), (-1;3), (-1,5;2,5), (-1;2), (-1;0), (0;-1), (2;-1,5), (3,5;-1,5), (5;-2)

Ландыш

(6,5;12), (6,75;11,5), (7;10,5), (6,5;10), (6,25;11), (6;10,5), (6,25;11,5), (6,5;12), (6,5;12,5), (5;10,5), (6;9,5)(6,5;8), (5,75;8,5), (5,5;7,5), (5,25;8,5), (4,5;8), (5;9,5), (5,5;10), (5;10,5), (3;8), (3,5;8),(4,5;7), (4,5;6,5),(5;5,5), (4,25;6), (4;5), (3,75;6), (3;5,5), (3,5;6,5), (3,5;7), (4;7,5), (3,5;8), (3;8), (1,5;6), (3;4,5), (3,5;3), (2,75;3,5), (2,5;2,5), (2,25;3,5), (1,5;3), (2;4,5), (2,5;5), (1,5;6), (0,5;0), (0,5;1,5), (1,5;7,5), (0,5;10,5), (-1,5;13), (-3;10,5), (-4;6), (-3,5;4), (0,5;0), (0;-3).

Машина

(-3,5;0,5), (-2,5;0,5), (-1,5;3,5), (0,5;3,5), (0,5;-0,5), (1;-0,5), (1;0), (1,5;0), (5,5;4), (5,75;4), (6,75;5), (5,5;5), (5,5;8), (8,5;5), (7,25;5), (6,25;4), (6,5;4), (4,5;2), (6;0) (6,5;0), (6,5;-1.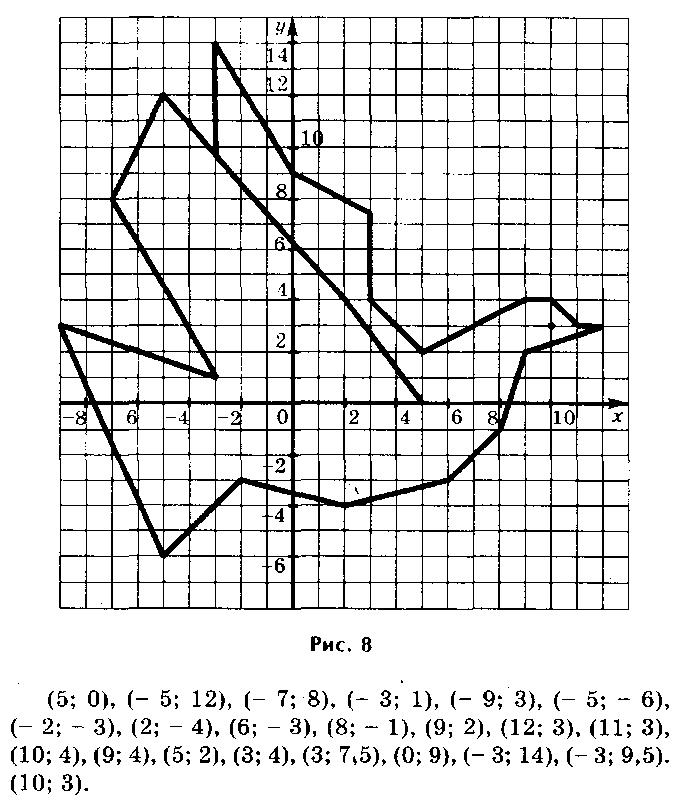 5),

(6;-1,5), (6;-2), (5,5;-2,5), (4,5;-2,5),(4;-2), (4;-1,5), (0;-1,5), (0;-2), (-0,5;-2,5), (-1.5;-2,5),

(-2;-2), (-2;-1.5), (-3,5;-1.5), (-3,5;0,5).

Кошечка

(-2;-7), (-4;-7), (-3;-5), (-6;-2), (-7;-3), (-7;6), (-6;5), (-4;5), (-3;6), (-3;3), (-4;2), (-3;1), (-1;3), (1;3), (4;1), (4;2), (3;6), (4;7), (5;7), (6;6), (5;1), (5;-5), (6;-6), (5;-7), (3;-7), (4;-5), (2;-3), (2;-2), (1;-1), (-1;-1),(-2;-2),(-1;-6), (-2;-7)

усы 1) (-9;5), (-5;3), (-2;2).

2) (-2;3), (-8;3),

3) (-9;2), (-5;3), (-1;5)

глаза (-6;4) и (-4;4)..

Рыбка

(-4;2), (-3;4), (2;4), (3;3), (5;2), (7;0), (5;-2), (3;-2), (2;-4), (0;-4), (-1;-2), (-5;0), (-7;-2), (-8;-1), (-7;1), (-8;3), (-7;4), (-5;2), (-2;2), (0;3), (3;3) и глаз (5;0).

Мышонок

(-6;-5), (-4,5;-4,5), (-3;-3,5), (-1,5;-2), (-2;1), (-2;0), (-1,5;1), (-1;1,5), (0,2), (0,5;2), (0,5;1,5), (0,5;2,5), (1;2,5), (1;2), (1,5;2), (2,5;1,5), (2,5;1), (1,5;1), (1,5;0,5), (2;0,5), (1,5;0), (1;0),

(0,5;-1), (0;-1,5), (1;-1,5), (0;-2), (-1,5;-2), глаз (1,5;1,5).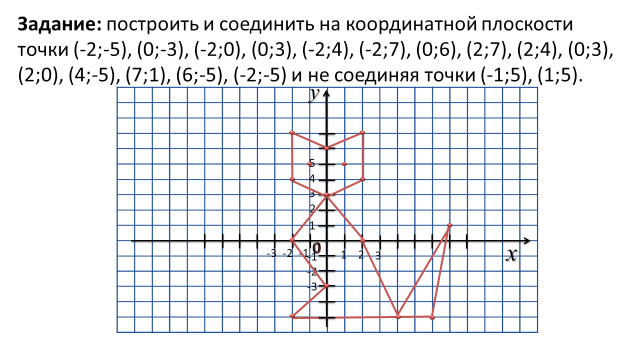

Лебедь

(2;12), (2;13), (3;13,5), (4;13,5), (5;13), (3;4), (8;4), (6;1), (3;1), (2;2), (2;4), (4;11), (4;12,5), (3,5;12,5), (2;11), (2;12), (3;12), и (3;3), (4;2), (6;2), и (2,5;12,5).

Петух

( 1,5;5.5), ( 2,5;3,5), (2; 3), (2,5; 3), (3; 3,5), (3;4,5), (2,5;5,5), (3,5;6), (2,5;6,5), (3;7), (2,5;7), (2,5;7), (2;7)(2;8), (1,5;7), (1,5;8,5), (1;7), (1;6,5), (0,5;6), (0,5;5), (-0,5;4), (-2,5;3), (-4,5;4),

(-5;5), (-4,5;6), (-5,5;8), (-6,5;8,5), (-7,5;8), (-8,5;7), (-9;6), (-9;4), (-8,5;2,5), (-8,5;1), (-8;0),

(-8;1), (-7,5;0,5), (-7,5;2), (-7;0,5), (-6,5;1,5), (-5,5;0,5), (-4,5;0), (-3,5;-2,5), (-3;-3), (-3;-5,5),

(-4;-5,5), (-3;-6), (-2;-6), (-2,5;-5,5), (-2,5;-4), (0;-1), (0;-0,5), (1;0), (2,5;1,5), (2,5;2,5), (2;3) и (-0,5;3), (-0,5;2,5), (-1,5;1), (-2,5;1), (-5;2,5), (-4,5;3), (-5;3,5), (-4,5;3,5)и (1,5;6,5).

Птенчик

(-1;-7), (-2;-8), (-5;-8), (-6;-7), (-5;-5), (-6;-5), (-7;-4), (-7,5;-4), (-8;-5), (-10;-6), (-9;-5), (-8;-3), (-9;-4), (-11;-5), (-9;-3), (-11;-4), (-9;-2), (-9;0), (-7;2), (-5;3), (-1,5;3), (-1,5;6), (-1;7), (1;8), (2;8), (4;10), (3;8), (3;7), (5;9), (4;7), (4,5;6), (4,5;4), (3;2), (2,5;1), (2,5;-2), (2;-3), (1;-4),

(-1;-5), (-2;-5), (-2;-5,5), (-1;-6), (1;-6), (0;-7), (-3;-7), (-3;-5), (-4;-5), (-4,5;-6), (-3;-7) и глаз (1,5;7).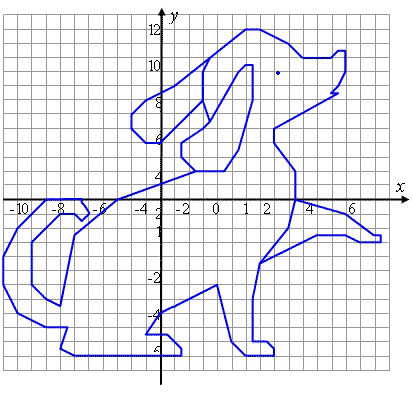

Дельфин

(-7;-2), (-3;4), (-1;4), (2;7), (2;4), (5;4), (9;-5), (10;-9), (8;-8), (5;-10), (7;-5), (3;-2), (-7;-2).ю ласт (0;0), (0;2),(2;1), (3;0), (0;0) и глаз (-4;0), (-4;1), (-3;1), (-3;0), (-4;0).

Петушок-золотой гребешок

(1;-5), (2;-4), (2;-1), (1;-1), (-4;4), (-4;8), (-5;9), (-7;9), (-4;11), (-5;12), (-5;13), (-4;12), (-3;13), (-2;12), (-1;13), (-1;12), (-2;11), (-1;10), (-2;6), (-1;5), (4;5), (1;10), (4;13), (8;13), (9;10), (7;11), (9;8), (7;8), (9;6), (8;6), (3;-1), (3;-4), (4;-5), (1;-5) соединить (-4;11) и (-2;11), глаз (-4;10), крыло (0;1), (0;3), (1;4), (2;4), (4;1), (2;1), (0;1).

Слоник 2

(-6;-1), (-5;-4), (-2;-6), (-1;-4), (0;-5), (1;-5), (3;-7), (2;-8), (0;-8), (0;-9), (3;-9), (4;-8), (4;-4),

(5;-6), (8;-4), (8;0), (6;2), (4;1), (0;1), (-2;2), (-6;-1), (-10;-2), (-13;-4), (-14;-7), (-16;-9),

(-13;-7), (-12;-10), (-13;-14),(-10;-14), (-10;-13), (-9;-13), (-10;-9), (-5;-9), (-5;-15), (-2;-15),

(-2;-13).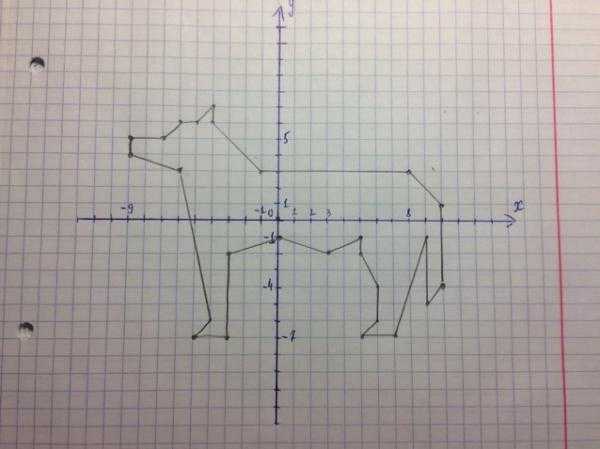 (-2;-10), (-1;-10), (-1;-11), (-2;-13), (0;-15), (2;-11), (2;-9) и глазки (0;-2) и (4;-2)

Слоник 3

(0;7), (4;8), (6;7), (8;6), (7;7), (6;9), (5;11), (5;12), (6;11), (7;12), (7;10), (10;7), (10;5), (8;3), (6;3), (7;2), (9;2), (9;1), (8;1), (7;0), (6;0), (7;-2), (8;-3), (8;-4), (10;-7,5), (9;-8), (7,5;-8), (7;-6), (5;-5), (6;-7), (4,5;-8), (4;-9), (2;-7), (3;-6), (2;-5) (1;-5,5), (0;-7), (0;-9), (-2;-10), (-3;-9,5), (-3,5;-8), (-5;-10), (-6,5;-9), (-7;-7), (-6;-7), (-5;-5), (-6;-3), (-8;-4), (-6;0), (-4;1), (-3;3), (-3;5), (-4,5;6), (-5; 7,5), (-3; 7,5), (-2;7), (-2;8), (0;7) и глаз (5;5)

Котик

а) (9,5;8), (11;8), (12;8,5), (12;11), (12,5;13), (14;14), (15;13), (15;9), (14,5;7), (13,5;3), (12;1,5), (11;1), (10;1,5), (10;2), (10,5;2,5), (11;2,5), (11;3),(10,5;4), (11;5), (6;5,5), (7;3), (6;2,5), (6;1.5), (7;1), (8,5;1,5), (9;2), (9;4), (10;3,5), (10,7;3,5) ;

б) (7,6), (7,5;6,5), (9;7), (9,5;8), (10;8,5), (9,5;8,5), (10;9), (10;10), (6,5;7), (2;6), (3,5;6), (2,5;5,5), (4;5,5), (3,5;5),(4,5;5), (6,5;6), (7;6)

в) (3,5;6,5), (3;7,5), (2;8), (2;10,5), (3;9,5), (4;10,5), (5;11), (6;11), (7;12), (8,5;13), (8,5;12), (9,5;10), (9,5;9,5)

г) глаза (4,5;8) окружность R=5мм и окружность =6мм

(7;9) окружность r=2мм и окружность R=6мм

нос (6,5;7) полукруг

рот (6,5;8) окружность R=2мм

Звезда

(-9;2), (-3;3), (0;8), (3;3), (9;2), (5;-3), (6;-9), (0;-7), (-6;-9), (-5;-3), (-9;2).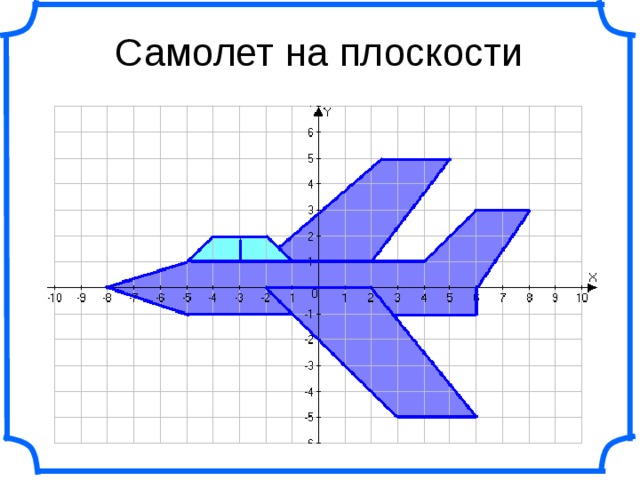

Орёл

а) (6;-5), (6,4;-4), (6;-3), (5;-0,5), (4;1), (4;2), (6;5), (6;7), (6;9), (7;13), (7;14), (6;13), (6,3;16), (6,5;15), (6;17), (4,5;14), (4,2;15), (3,5;13), (3,5;16), (3;14), (3;12), (1;7), (0,5;5), (1;4), (2;2), (2,5;1), (4;1) ,

б) (0,5;5), (-0,5;6), (-1;7), (-1,2;9), (-2;11), (-2;13), (-1;16,5), (-3;14), (-2;17), (-1;19), (-1;20),

(-3;17), (-3;18), (-2;21), (-4;18), (-4;20), (-5,5;17,5), (-5;19), (-6;18), (-7;10), (-6,5;7), (-6;5),

(-5;3), (-4;1), (-3;0,5), (-4;-2), (-6;-5), (-5;-5), (-7;-8), (-9;-11), (-7;-10), (-7,5;-13), (-6;-11),

(-6;-13), (-5;-11), (-5;-12), (-3;-7), (-3;-9), (-4;-10), (-3,5;-10,2), (-4;-11), (-2;-9), (-2;-9,2),

(-1;-9), (-2,3;-10,2), (-1,8;-10,3), (-2;-11,5), (-1;-11), (-0,5;-9), (-1;-7), (0;-6), (1;-4), (3;-4), (5;-4,4), (6;-5) глаз: (5;-3,5)

Дракон

(-11;3), (-14;3), (-14;4), (-11;7), (-7;7), (-5;5), (-2;5), (3;4), (4;5), (7;4), (9;3), (15;3), (18;5), (19;7), (19;4), (16;1), (14;0), (10;-2), (7;0), (6;-1), (9;-4), (8;-5), (6;-6), (4;-8), (4;-10), (2;-9),

(1;-10), (1;-9), (-1;-9), (2;-7), (4;-4), (2;-2), (1;-2), (-1;-3), (-2;-4), (-5;-5), (-6;-6), (-8;-6),

(-10;-7), (-9;-5), (-11;-6), (-10;-4), (-7;-4), (-5;-3), (-4;-2), (-4;-1), (-5;0), (-7;0), (-8;1), (-9;1),

(-10;2), (-12;2), (-13;3). Правые лапки: (-4;-1), (-6;-2), (-8;-2),

(-9;-1), (-12;0), (-13;-2), (-12;-2), (-12;-4), (-11;-3), (-10;-4), (-10;-3), (-7;-4), (2;-2), (1;-4),

(6;-6), (2;-10), (3;-10), (3;-11), (4;-11), (4;-12), (5;-11), (6;-12), (7;-10), (8;-10), (7;-9), (7;-7), (6;-6). Глаз:(-11;5), (-10;5), (-10;-6), (-11;5).

Дополнение к рисунку: (1;0), (2;-2), (-1;0), (-1;-3), (-5;0), (-5;1).

Слон

(-6;-1), (-5;-4), (-2;-6), (-1;-4), (0;-5), (1;-5), (3;-7), (2;-8), (0;-8), (0;-9), (3;-9), (4;-8), (4;-4),

(5;-6), (8;-4), (8;0), (6;2), (4;1), (0;1), (-2;2), (-6;-1), (-10;-2), (-13;-4), (-14;-7), (-16;-9),

(-13;-7), (-12;-10), (-13;-14), (-10;-14), (-10;-13), (-9;-13), (-10;-9), (-5;-9), (-5;-15), (-2;-15),

(-2;-13), (-2;-10), (-1;-10), (-1;-11), (-2;-13), (0;-15), (2;-11). (2;-9) и (0;-2) и (4;-2).

Страус

(0;0), (-3;-1), (-4;-4), (-4;-8), (-6;-10), (-6;-8,5), (-5;-7), (-5;-1), (-3;1), (-1;2), (-2;3), (-3;5),

(-5;3), (-5;5), (-7;3), (-7;5), (-9;2), (-9;5), (-6;8), (-4;8), (-3;6), (-1;7), (1;7), (0;9), (-3;8), (0;10), (-3;10), (0,12), (-3;12), (-1;13), (2;13), (0;15), (2;15), (4;14), (6;12), (5;10), (4;9), (3;7), (7;5), (9;8), (9;11), (7;14), (7;16), (9;17), (10;17), (11;16), (14;15), (10;15), (14;14), (11;14), (10;13), (11;11), (11;8), (10;5), (8;2), (7;1), (4;0), (2;-2), (3;-4), (4;-5), (6;-6), (8;-8), (9;-10), (7,5;-9),

(7;-8), (6;-7), (2;-5), (1;-3), (0;0), глаз (9,5;16)

Собака

(-7;4,5), (-8;5), (-10,5;3,5), (-10;3), (-7;4,5), (-5;5,5), (-5,5;8), (-5;8), (-4,5;6), (-4;6), (-3;8),

(-2,5;8), (-3;6), (-2,5;5,5), (-3;4,5), (-2;2), (0;1), (4,5;0), (7;4), (8;4), (5,5;0), (6;-5), (4,5;-6),

(4;-5), (4,5;-4,5), (4;-4), (3,5;-3), (4;-4), (3;-6), (-1,5;-6), (1,5;-5,5), (2,5;-5), (2,5;-4,5), (3,5;-3,5), (2,5;-4,5), (2;-5), (2;-4), (1;-5), (1;-4,5), (0;-5), (0;-6), (-2;-6), (-1,5;-5), (-1;-5), (-1;-4,5),

(-2;-4,5), (-2,5;-6), (-4;-5), (-3,5;-2,5), (-3;-2,5), (-3,5;-4), (-4;-1), (-4,5;0,5), (-4,5;1), (-5,5;0),

(-6;0,5), (-6,5;-1), (-8;0), (-9;-1), (-10;3), глаз: (-5,5;3,5), (-5,5;4,5), (-4,5;4,5), (-4,5;3,5),

(-5,5;3,5).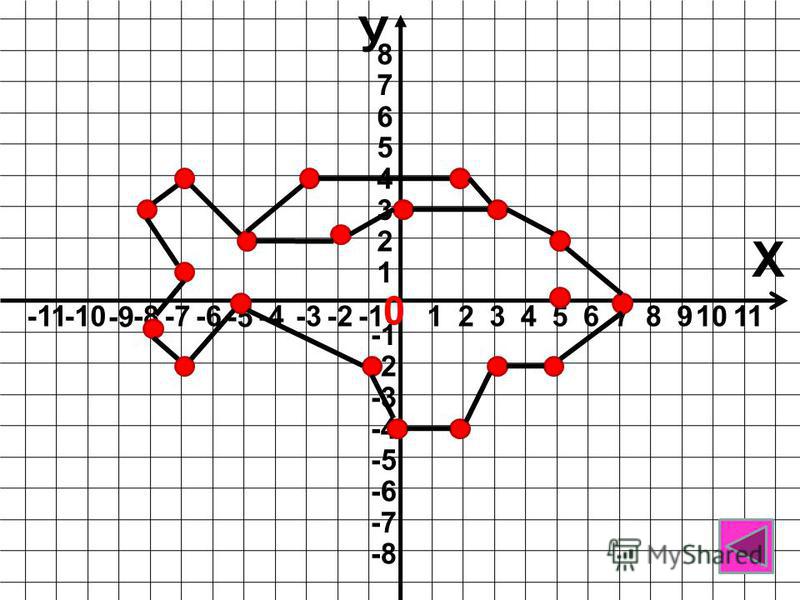

Кит

(4;-0,5), (6,5;-2), (-2;-3), (-10,5;4), (-12,5;7,5), (-9;11), (-13;10), (-17;11), (-12,5;7,5), (-10,5;4), (-3;2), (1;4,5), (7,5;3), (6,5;-2), глаз: (4;2).

Заяц

(1;7), (0;10), (-1;11), (-2;10), (0;7), (-2;5), (-7;3), (-8;0), (-9;1), (-9;0), (-7;-2), (-2;-2), (-3;-1),

(-4;-1), (-1;3), (0;-2), (1;-2), (0;0), (0;3), (1;4), (2;4), (3;5), (2;6), (1;9), (0;10), глаз (1;6)

Жираф

(-2;-14), (-3;-14), (-3,5;-10), (-3,5;0), (-4;2), (-7;16,5), (-8;16,5), (-11;17), (-11;17,5), (-9;18),

(-7,519), (-6,5;20), (-6;19,5), (-6;19), (-5;18), (-4;13,5), (0;5), (6;3), (8;0), (6;2), (7;0), (8;-5), (9,5;-14), (8,5;-14), (7,5;-8,5), (4,5;-3,5), (0,5;-3,5), (-1;-5,5), (-1,5;-9), (-2;-14), глаз: (-8;20).

Мышонок

(-6;-5), (-4,5;-4,5), (-3;-3,5), (-1,5;-2), (-2;1), (-2;0), (-1,5;1), (-1;1,5), (0,2), (0,5;2), (0,5;1,5), (0,5;2,5), (1;2,5), (1;2), (1,5;2), (2,5;1,5), (2,5;1), (1,5;1), (1,5;0,5), (2;0,5), (1,5;0), (1;0),

(0,5;-1), (0;-1,5), (1;-1,5), (0;-2), (-1,5;-2), глаз (1,5;1,5).

Лебедь

(2;12), (2;13), (3;13,5), (4;13,5), (5;13), (3;4), (8;4), (6;1), (3;1), (2;2), (2;4), (4;11), (4;12,5), (3,5;12,5), (2;11), (2;12), (3;12), и (3;3), (4;2), (6;2), и (2,5;12,5).

Ракета

(-3;-13),(-6;-13), (-3;-5), (-3;6), (0;10), (3;6), (3;-5), (6;-13), (3;-13), (3;-8), (1;-8), (2;-13),

(-2;-13), (-1;-8) (-3;-8), (-3;-13).

Самолет

(-7;0), (-5;2), (7;2), (9;5), (10;5), (10;1), (9;0), (-7;0),

(0;2), (5;6), (7;6), (4;2),

(0;1), (6;-3), (8;-3), (4;1), (0;1).

систем координат изображения
— MATLAB & Simulink

Системы координат изображения

Вы можете получить доступ к местоположениям на изображениях, используя несколько различных систем координат изображения.
Вы можете указывать местоположения, используя дискретные пиксельные индексы, потому что изображения хранятся как
массивы. Вы также можете указать местоположения, используя непрерывные пространственные координаты, потому что
изображения представляют сцены реального мира в непрерывном пространстве.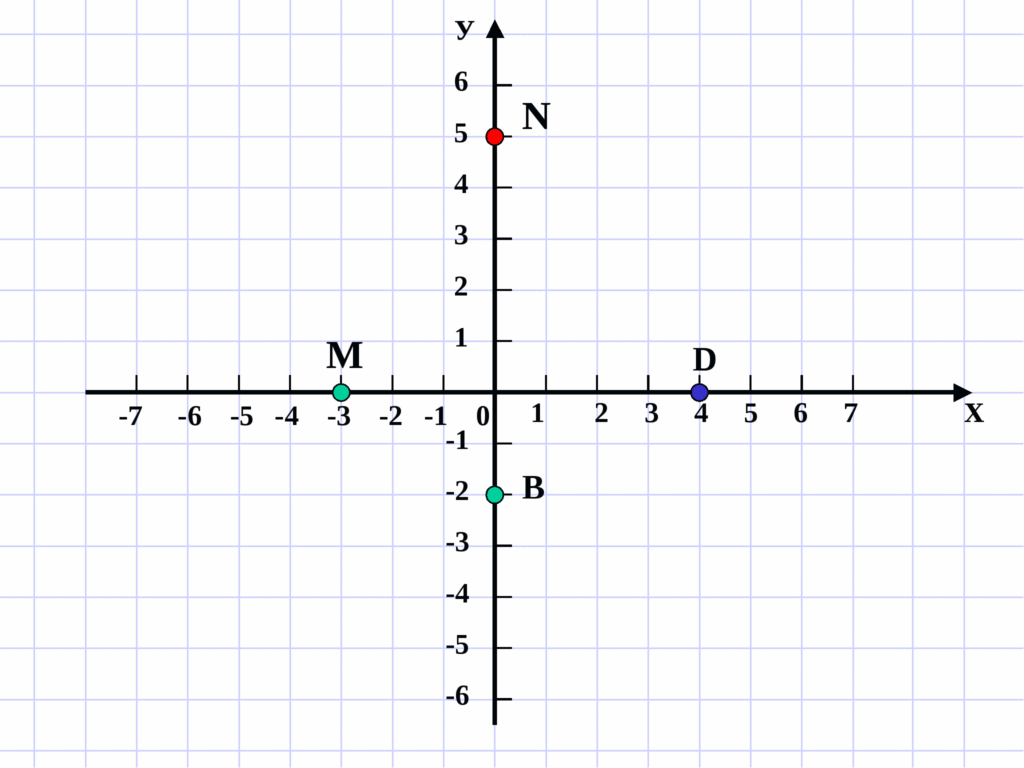

Индексы пикселей

Как описано в изображениях в MATLAB, MATLAB ^® хранит большинство изображений в виде массивов. Каждый (строка, столбец) индекс массива
соответствует одному пикселю отображаемого изображения.

Существует однозначное соответствие между индексами пикселей и нижними индексами для
первые два измерения матрицы. Подобно индексации массива в MATLAB, индексы пикселей являются целыми значениями и находятся в диапазоне от 1 до длины
строку или столбец. Индексы располагаются сверху вниз и слева направо.
Правильно.

Например, данные для пикселя в пятой строке, второй столбец хранятся в
матричный элемент (5,2). Вы используете обычную индексацию матрицы MATLAB для доступа к значениям отдельных пикселей. За
например, код MATLAB

 I(2,15) 

возвращает значение пикселя в строке 2 столбца 15 одноканального изображения.
я .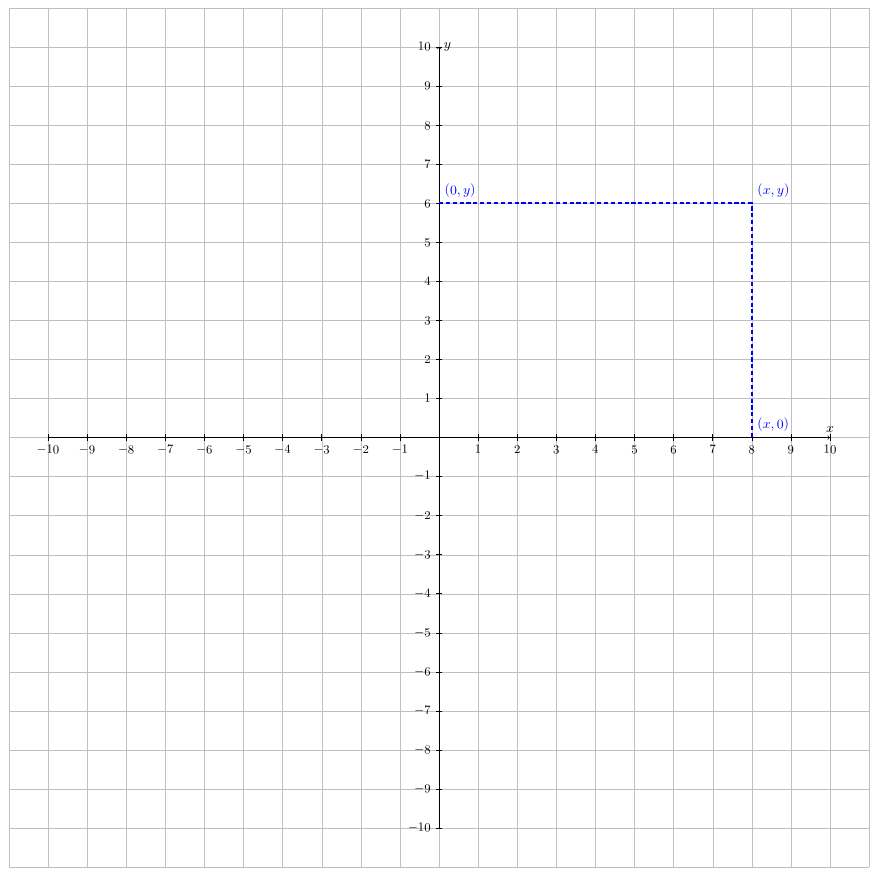 Точно так же код MATLAB

 RGB(2,15,:) 

возвращает значения цвета пикселя в строке 2, столбце 15 многоканального
изображение РГБ .

Пространственные координаты

В системе пространственных координат местоположения на изображении
положения на непрерывной плоскости. Места описываются в терминах декартовой
x и y координаты (не строки и столбца
индексы, как в системе индексации пикселей). С этой картезианской точки зрения
( x , y ) расположение, такое как (3.2,5.3)
осмысленной и отличной от координаты (5,3).

Image Processing Toolbox™ определяет два типа пространственных систем координат в зависимости от кадра
ссылки. Внутренние координаты задают местоположения по отношению к изображению.
точка зрения. Мировые координаты определяют местоположение по отношению к внешнему
мировой наблюдатель.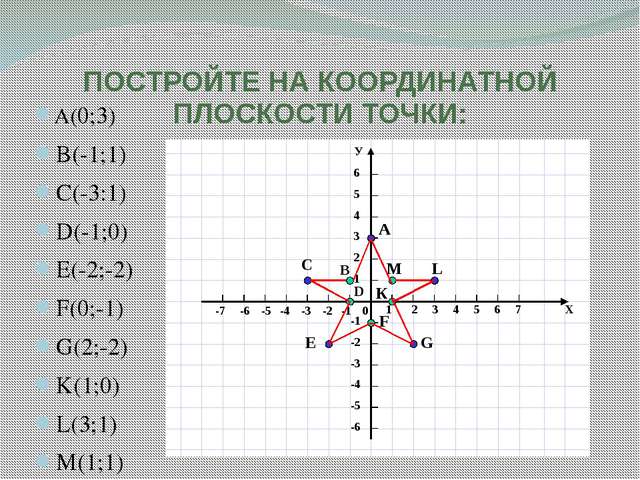

Внутренние координаты

По умолчанию набор инструментов определяет пространственные координаты изображения с помощью
внутренняя система координат . Эта пространственная координата
система соответствует индексам пикселей изображения. Внутренние координаты
( x , y ) центральной точки любого
пикселя идентичны индексам столбца и строки для этого пикселя. Например,
центральная точка пикселя в строке 5 столбца 3 имеет пространственные координаты
х = 3,0, у = 5,0. Имейте в виду,
однако порядок внутренних координат (3.0,5.0) обратный относительно
индексам пикселей (5,3).

Внутренние координаты центра каждого пикселя имеют целочисленное значение.
центр верхнего левого пикселя имеет внутренние координаты (1.0, 1.0). Центр
нижнего правого пикселя имеет внутренние координаты ( numCols ,
numRows ), где numCols и
numRows — количество строк и столбцов в изображении.
Как правило, центр пикселя с индексами пикселей ( м ,
n ) попадает в точку х =
n , y = м в
внутреннюю систему координат.

Поскольку размер каждого пикселя во внутренней системе координат составляет одну единицу,
границы изображения имеют дробные координаты. Верхний левый угол
изображения находится в (0,5,0,5), а не в (0,0). Аналогично, нижний правый
угол изображения находится в точке ( numCols + 0,5,
numRows + 0,5).

Некоторые функции в основном работают с пространственными координатами, а не с пикселями
индексы, но пока вы используете систему пространственных координат по умолчанию
(внутренние координаты), вы можете указать местоположения с точки зрения их столбцов
( x ) и строки ( y ).

Мировые координаты

В некоторых ситуациях вы можете использовать мировая координата
система (также называемая системой пространственных координат не по умолчанию). Немного
ситуации, когда вы можете захотеть использовать мировую систему координат, включают:

• При выполнении геометрической операции, например переноса, на
  изображение и хотите сохранить информацию о том, как новая позиция
  относится к исходному положению.

• Когда пиксели не квадратные. Например, в магнитном резонансе
  визуализация (МРТ), данные, которые вы можете собирать, чтобы пиксели имели
  более высокая частота дискретизации в одном направлении, чем в ортогональном направлении.

• Когда вы знаете, как экстент пикселей выравнивается с позициями в
  реальный мир. Например, на аэрофотоснимке каждый пиксель
  может покрывать определенный участок земли размером 5 на 5 метров.

• Если вы хотите изменить направление
  x — ось или y — ось. Это
  общий метод для использования с геопространственными данными.

Существует несколько способов определения мировой системы координат. Вы можете использовать
объекты пространственной привязки, которые кодируют местоположение изображения в мире
систему координат, разрешение изображения и то, как экстент изображения связан с
внутренние и мировые координаты. Вы также можете указать максимальное и минимальное
координаты в каждом измерении. Дополнительные сведения см. в разделе Определение мировой системы координат изображения.

Связанные примеры

• Сдвиг диапазона X- и Y-координат отображаемого изображения

Подробнее о

• Изображения в MATLAB
• Определить мировую систему координат изображения
  • Системы координат изображения
  • Предварительный просмотр элемента набора данных мозаики

  Система координат изображения (ICS) отображает ваши изображения без искажений. Он может это сделать, потому что система координат фрейма данных такая же, как та, в которой были захвачены ваши изображения. Так как изображения в системе координат изображения не искажены, он идеально подходит для использования с наклонными изображениями и измерениями. Системы координат изображения поддерживаются в ArcMap и REST API сервисов изображений ArcGIS Server.

  Координаты изображения доступны на изображениях, которые содержат информацию о преобразовании сенсора, такую ​​как коэффициенты рационального полинома (RPC) или кадровые камеры. Система координат изображения состоит из домена (исходного экстента), преобразований геоданных и информации о пространственной привязке карты из соответствующего изображения.

  Системы координат изображения

  Как правило, ваш фрейм данных использует систему координат карты. Это означает, что пиксели вашего изображения преобразуются в координаты карты с использованием сенсорных моделей и проекций. Преобразование ваших изображений в координаты карты может привести к тому, что ваши изображения будут выглядеть перекошенными или искаженными.
  из-за различных используемых преобразований и поправок на рельеф, особенно для наклонных изображений.

  При использовании системы координат изображения можно настроить фрейм данных на использование системы координат одного изображения для установления координат.
  система для фрейма картографических данных. Это изображение отображается неискаженным в исходном виде без необходимости различных преобразований и проекций.
  Все
  другие изображения, функции, ярлыки,
  и аннотации проецируются для наложения этого изображения в его координатах изображения.
  Система.

  Для работы с системами координат изображения в ArcMap используйте окно Анализ изображения.

  1. в
     В окне Анализ изображения выделите растровое изображение, на основе которого будет создана система координат изображения.
  2. Щелкните слой правой кнопкой мыши и выберите «Фокус на изображении».

     Если изображение, которое вы щелкнули, не имеет связанной с ним системы координат изображения, параметр «Фокус на изображении» недоступен.

  Координата кадра данных будет установлена ​​с координатой выбранного изображения. Изображение и слои на карте будут отображаться в одних и тех же координатах.

  Примечание:

  Чтобы вернуть фрейм данных обратно к координатам карты, щелкните Фокус на изображении/Фокус на сервисе изображений, чтобы снять флажок.

  Система координат изображения может быть выбрана только для одного изображения в кадре данных. Это означает, что только одно изображение в наборе данных мозаики может использоваться для установки системы координат. Ниже приведены шаги по установке системы координат изображения для изображения в наборе данных мозаики.

  1. Сделайте выбор в наборе данных мозаики.
  2. В оглавлении щелкните правой кнопкой мыши подслой Footprint и выберите «Добавить выбранные растры на карту».

  Теперь каждый отдельный растровый слой можно установить в качестве изображения фокуса.

  Предварительный просмотр элемента набора данных мозаики

  Каждый элемент набора данных мозаики имеет собственное окно свойств.