Обозначение в кинематике: Обозначения кинематических схем
Содержание
Обозначения кинематических схем
Обозначения кинематических схем
В данной статье приведены наиболее употребительные условные обозначения элементов кинематических схем металлорежущих станков. Приведены изображения элементов различных кинематических схем и их описание. Условные обозначения элементов утверждены ГОСТ 2.770-68, ГОСТ 2.782-68 и ГОСТ 2.782-68.
Обозначения кинематических схем. Смотреть в увеличенном масштабе
- общее обозначение двигателя без уточнения типа
- общее обозначение электродвигателя
- электродвигатель на лапах
- электродвигатель фланцевый
- электродвигатель встроенный
- вал, ось, стержень, шатун и т. п.
- конец шпинделя для центровых работ
- конец шпинделя для патронных работ
- конец шпинделя для работ с цанговым патроном
- конец шпинделя для сверлильных работ
- конец шпинделя для расточных работ с планшайбой
- конец шпинделя для фрезерных работ
- конец шпинделя для кругло-, плоско- и резьбошлифовальных работ
- ходовой винт для передачи движения
- неразъемная маточная гайка скольжения
- неразъемная маточная гайка с шариками
- разъемная маточная гайка скольжения
- радиальный подшипник без уточнения типа
- радиально-упорный односторонний подшипник без уточнения типа
- радиально-упорный двусторонний подшипник без уточнения типа
- упорный односторонний подшипник без уточнения типа
- упорный двусторонний подшипник без уточнения типа
- радиальный подшипник скольжения
- радиальный самоустанавливающийся подшипник скольжения
- радиально-упорный односторонний подшипник скольжения
- радиально-упорный двусторонний подшипник скольжения
- упорный односторонний подшипник скольжения
- упорный односторонний подшипник скольжения
- упорный двусторонний подшипник скольжения
- упорный двусторонний подшипник скольжения
- радиальный подшипник качения (общее обозначение)
- радиальный роликовый подшипник
- радиальный самоустанавливающийся подшипник качения
- радиально-упорный односторонний подшипник качения
- радиально-упорный односторонний подшипник качения
- радиально-упорный двусторонний подшипник качения
- радиально-упорный двусторонний подшипник качения
- радиально-упорный роликовый односторонний подшипник
- упорный односторонний подшипник качения
- упорный односторонний подшипник качения
- упорный двусторонний подшипник качения
- свободное для вращения соединение детали с валом
- подвижное вдоль оси соединение детали с валом
- соединение детали с валом посредством вытяжной шпонки
- глухое, неподвижное соединение детали с валом
- глухое жесткое соединение двух соосных валов
- глухое соединение валов с предохранением от перегрузки
- эластичное соединение двух соосных валов
- шарнирное соединение валов
- телескопическое соединение валов
- соединение двух валов посредством плавающей муфты
- соединение двух валов посредством зубчатой муфты
- соединение двух валов предохранительной муфтой
- кулачковая односторонняя муфта сцепления
- кулачковая двусторонняя муфта сцепления
- фрикционная муфта сцепления (без уточнения вида и типа)
- фрикционная односторонняя муфта (общее обозначение)
- фрикционная односторонняя электромагнитная муфта
- фрикционная односторонняя гидравлическая или пневматическая муфта (общее обозначение)
- фрикционная двусторонняя муфта (общее обозначение)
- фрикционная двусторонняя электромагнитная муфта
- фрикционная двусторонняя гидравлическая или пневматическая муфта (общее обозначение)
- фрикционная конусная односторонняя муфта
- фрикционная конусная двусторонняя муфта
- фрикционная дисковая односторонняя муфта
- фрикционная дисковая двусторонняя муфта
- фрикционная муфта с колодками
- фрикционная муфта с разжимным кольцом
- самовыключающая односторонняя муфта обгона
- самовыключающая двусторонняя муфта обгона
- самовыключающая центробежная муфта
- тормоз конусный
- тормоз колодочный
- тормоз ленточный
- тормоз дисковый
- тормоз дисковый электромагнитный
- тормоз дисковый гидравлический или пневматический
- шарнирное соединение стержня с неподвижной опорой с движением только в плоскости чертежа
- соединение стержня с опорой шаровым шарниром
- маховик, жестко установленный на валу
- эксцентрик, установленный на конце вала
- конец вала под съемную рукоятку
- рычаг переключения
- рукоятка, закрепленная на конце вала
- маховичок, закрепленный на конце вала
- передвижные упоры
- шарнирное соединение кривошипа
Обозначения кинематических схем. Смотреть в увеличенном масштабе
Смотреть в увеличенном масштабе
- 87а — шарнирное соединение кривошипа постоянного радиуса с шатуном
- 87б — шарнирное соединение кривошипа переменного радиуса с шатуном
- 87в — шарнирное соединение кривошипа постоянного радиуса с шатуном
- 87г — шарнирное соединение кривошипа переменного радиуса с шатуном
- 88а — шарнирное соединение одноколейного вала с шатуном
- 88б — шарнирное соединение многоколенного вала с шатуном
- 88в — коленвал с жестким противовесом
- 88г — коленвал с маятниковым противовесом
- 89а — кривошипно-кулисный механизм с поступательно движущейся кулисой
- 89б — кривошипно-кулисный механизм с вращающейся кулисой
- 89в — кривошипно-кулисный механизм с качающейся кулисой
- 126а — коническая зубчатая передача между пересекающимися валами (общее обозначение без уточнения типа)
- 126б — коническая зубчатая передача соответственно с прямыми, спиральными и круговыми зубьями
- 133а — червячная глобоидная передача
- 133б — червячная передача с цилиндрическим червяком
Пример кинематической схемы токарно-винторезного станка. Смотреть в увеличенном масштабе
Смотреть в увеличенном масштабе
Кучер А. М., Киватицкий М. М., Покровский А. А. Металлорежущие станки (альбом кинематических схем и узлов). Изд-во «Машиностроение», 1972.
Читайте также: Регулирование токарно-винторезного станка 16К20
Полезные ссылки по теме. Дополнительная информация
Обозначение элементов кинематических схем
Конструкторы, разрабатывающие различные машины и механизмы, часто выполняют кинематические схемы. При этом они руководствуются нормами и требованиями, изложенными в таком основополагающем документе, как ГОСТ 2.770–68.
В технике под схемой понимается графическое изображение, на котором показаны составные части изделия, их конструктивные особенности, а также существующие между ними связи с помощью упрощенных обозначений и символов. В составе пакетов конструкторской документации схемы играют достаточно важную роль. Они наличествуют как в общих описаниях изделий, инструкциях по их установке, наладке и эксплуатации.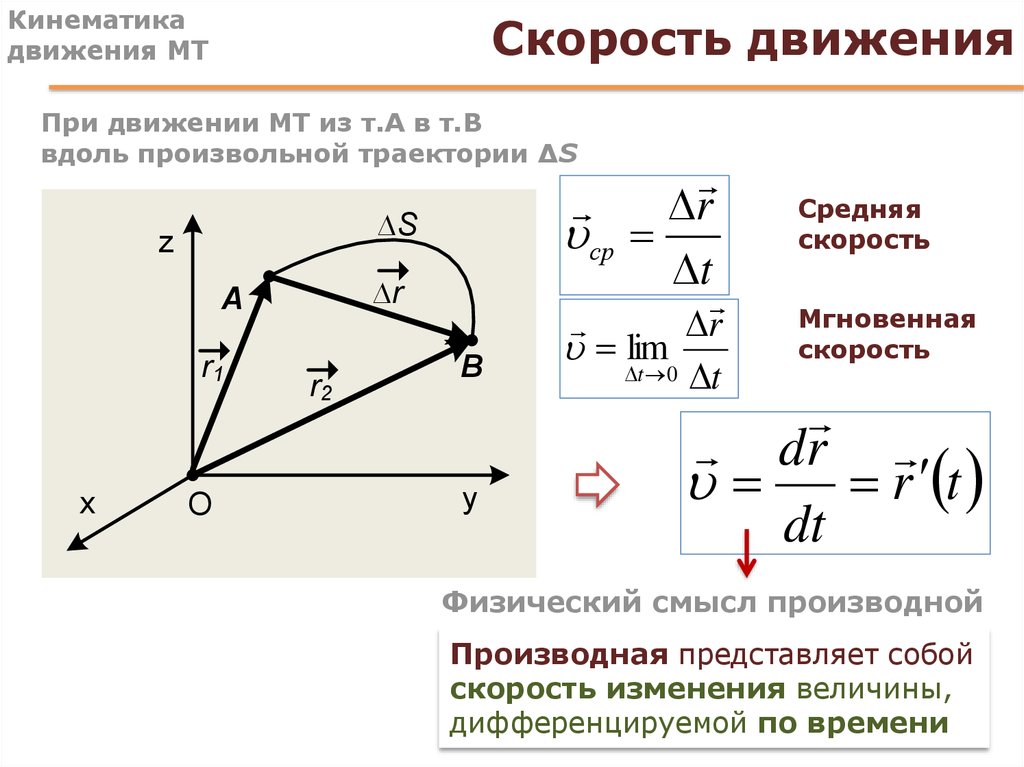 Схематические чертежи оказывают неоценимую помощь персоналу, занимающемуся монтажом, пуско-наладкой, ремонтом машин, механизмов и отдельных агрегатов. Схемы дают возможность быстро разобраться в том, каковы функциональные связи существуют между механическими, гидравлическими, электрическими и другими звеньями и системами технических устройств.
Схематические чертежи оказывают неоценимую помощь персоналу, занимающемуся монтажом, пуско-наладкой, ремонтом машин, механизмов и отдельных агрегатов. Схемы дают возможность быстро разобраться в том, каковы функциональные связи существуют между механическими, гидравлическими, электрическими и другими звеньями и системами технических устройств.
Когда разработка какой-либо машины только начинается, конструкторы от руки вычерчивают общий набросок будущего изделия, то есть составляют его первоначальную схему. На ней условно отображаются все основные узлы, а также показываются взаимосвязи между ними. Только после того, как принципиальная схема устройства отработана, начинается разработка чертежей и прочей конструкторской документации.
В современном машиностроении наибольшее применение находят те машины, в которых передача движения основывается на механическом, гидравлическом или электрическом принципе функционирования.
Предназначением кинематических схем является отражение той связи, в которой состоят рабочий механизм и привод. Следует отметить, что в современных автомобилях, станочном и прочем технологическом оборудовании механические передачи отличаются большой сложностью и содержат множество элементов. Поэтому для того, чтобы правильно создавать схемы таких конструкций, нужно прекрасно знать все условности, которые используются для графического изображения принципа работы машины или механизма без того, чтобы уточнять их конструктивные особенности. К примеру, кинематические схемы станочного оборудования отражают то, каким именно образом вращательное движение вала электродвигателя сообщается шпинделю, причем контур станка показывается (или не показывается) тонкой линией.
Следует отметить, что в современных автомобилях, станочном и прочем технологическом оборудовании механические передачи отличаются большой сложностью и содержат множество элементов. Поэтому для того, чтобы правильно создавать схемы таких конструкций, нужно прекрасно знать все условности, которые используются для графического изображения принципа работы машины или механизма без того, чтобы уточнять их конструктивные особенности. К примеру, кинематические схемы станочного оборудования отражают то, каким именно образом вращательное движение вала электродвигателя сообщается шпинделю, причем контур станка показывается (или не показывается) тонкой линией.
Если на схемах используются нестандартизованые условные обозначения, то они требуют пояснений. Что касается внешних очертаний и схематических разрезов, то на схемах они изображаются упрощенно, в соответствии с тем, какую именно конструкцию имеет каждый элемент изделия.
На схематических изображениях от каждой составной их части проводятся линии-выноски.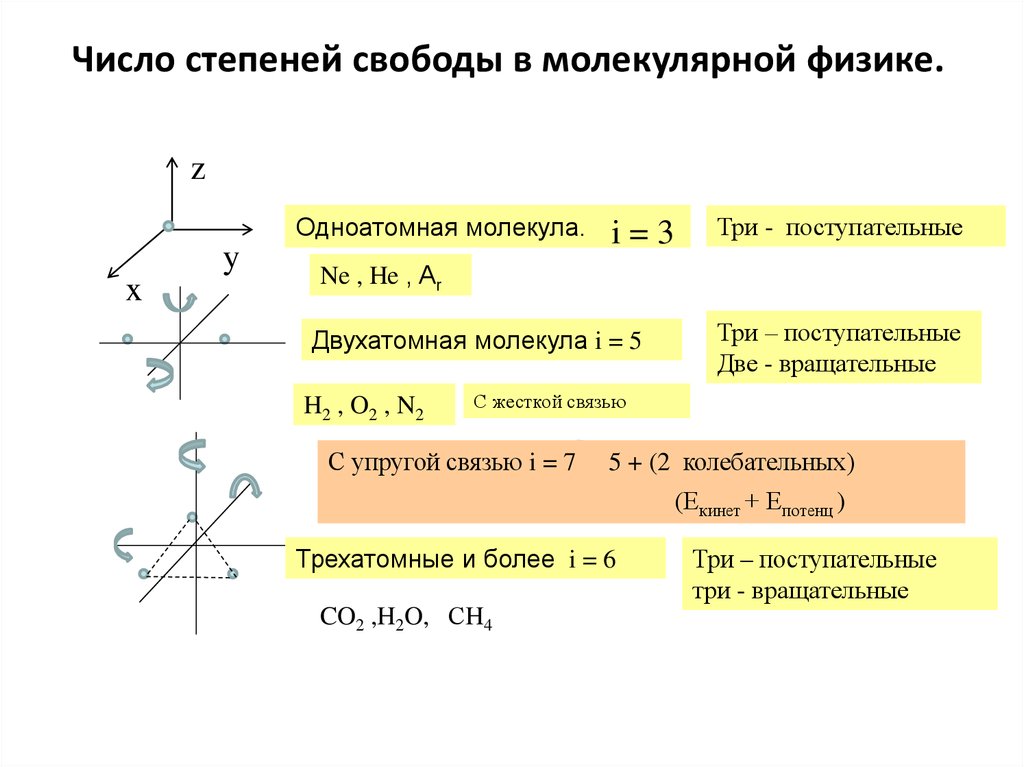 От сплошных линий они начинаются стрелками, а от плоскостей – точками. На полках линий-выносок указываются порядковые номера позиций. При этом для таких элементов, как валы, используются римские цифры, а для остальных – арабские цифры. Под полками линий-выносок указываются параметры и основные характеристики составных частей схем.
От сплошных линий они начинаются стрелками, а от плоскостей – точками. На полках линий-выносок указываются порядковые номера позиций. При этом для таких элементов, как валы, используются римские цифры, а для остальных – арабские цифры. Под полками линий-выносок указываются параметры и основные характеристики составных частей схем.
Кинематические уравнения
Целью этого первого раздела Класса физики было исследование разнообразных средств, с помощью которых можно описать движение объектов. Разнообразие репрезентаций, которые мы исследовали, включает словесные репрезентации, графические репрезентации, числовые репрезентации и графические репрезентации (графики положение-время и графики скорость-время). В Уроке 6 мы исследуем использование уравнений для описания и представления движения объектов. Эти уравнения известны как кинематические уравнения.
Существует множество величин, связанных с движением объектов: перемещение (и расстояние), скорость (и скорость), ускорение и время. Знание каждой из этих величин дает описательную информацию о движении объекта. Например, если известно, что автомобиль движется с постоянной скоростью 22,0 м/с, на север в течение 12,0 секунд при смещении на север на 264 метра, то движение автомобиля полностью описано. И если известно, что вторая машина разгоняется из положения покоя с ускорением в восточном направлении 3,0 м/с 2 за время 8,0 секунд, обеспечивая конечную скорость 24 м/с, восток и смещение в восточном направлении 96 метров, то движение этого автомобиля полностью описано. Эти два утверждения обеспечивают полное описание движения объекта. Однако такая полнота не всегда известна. Часто бывает известно лишь несколько параметров движения объекта, а остальные неизвестны. Например, приближаясь к светофору, вы можете знать, что скорость вашего автомобиля составляет 22 м/с на восток, а ускорение заноса составляет 8,0 м/с.0006 2 , Запад. Однако вы не знаете, какое смещение испытает ваша машина, если вы нажмете на тормоза и занесете до остановки; и вы не знаете время, необходимое для остановки.
Знание каждой из этих величин дает описательную информацию о движении объекта. Например, если известно, что автомобиль движется с постоянной скоростью 22,0 м/с, на север в течение 12,0 секунд при смещении на север на 264 метра, то движение автомобиля полностью описано. И если известно, что вторая машина разгоняется из положения покоя с ускорением в восточном направлении 3,0 м/с 2 за время 8,0 секунд, обеспечивая конечную скорость 24 м/с, восток и смещение в восточном направлении 96 метров, то движение этого автомобиля полностью описано. Эти два утверждения обеспечивают полное описание движения объекта. Однако такая полнота не всегда известна. Часто бывает известно лишь несколько параметров движения объекта, а остальные неизвестны. Например, приближаясь к светофору, вы можете знать, что скорость вашего автомобиля составляет 22 м/с на восток, а ускорение заноса составляет 8,0 м/с.0006 2 , Запад. Однако вы не знаете, какое смещение испытает ваша машина, если вы нажмете на тормоза и занесете до остановки; и вы не знаете время, необходимое для остановки. В таком случае неизвестные параметры могут быть определены с использованием принципов физики и математических уравнений (кинематических уравнений).
В таком случае неизвестные параметры могут быть определены с использованием принципов физики и математических уравнений (кинематических уравнений).
БОЛЬШАЯ 4
Кинематические уравнения представляют собой набор из четырех уравнений, которые можно использовать для прогнозирования неизвестной информации о движении объекта, если известна другая информация. Уравнения можно использовать для любого движения, которое можно описать либо как движение с постоянной скоростью (ускорение 0 м/с/с), либо как движение с постоянным ускорением. Они никогда не могут быть использованы в течение какого-либо периода времени, в течение которого изменяется ускорение. Каждое из кинематических уравнений включает четыре переменные. Если известны значения трех из четырех переменных, то можно вычислить значение четвертой переменной. Таким образом, кинематические уравнения обеспечивают полезные средства прогнозирования информации о движении объекта, если известна другая информация. Например, если известно значение ускорения, а также значения начальной и конечной скорости буксующего автомобиля, то перемещение автомобиля и время можно предсказать с помощью кинематических уравнений. Урок 6 этого раздела будет посвящен использованию кинематических уравнений для предсказания числовых значений неизвестных величин движения объекта.
Например, если известно значение ускорения, а также значения начальной и конечной скорости буксующего автомобиля, то перемещение автомобиля и время можно предсказать с помощью кинематических уравнений. Урок 6 этого раздела будет посвящен использованию кинематических уравнений для предсказания числовых значений неизвестных величин движения объекта.
Четыре кинематических уравнения, описывающие движение объекта:
В приведенных выше уравнениях используются различные символы. Каждый символ имеет свое особое значение. Символ d обозначает смещение объекта. Символ t обозначает время, в течение которого объект перемещался. Символ a обозначает ускорение объекта. А символ v обозначает скорость объекта; нижний индекс i после v (как в v i ) указывает, что значение скорости является начальным значением скорости, а нижний индекс f (как в v f ) указывает, что значение скорости является окончательным значением скорости.
Каждое из этих четырех уравнений надлежащим образом описывает математическую связь между параметрами движения объекта. Таким образом, их можно использовать для прогнозирования неизвестной информации о движении объекта, если известна другая информация. В следующей части Урока 6 мы исследуем этот процесс.
Таким образом, их можно использовать для прогнозирования неизвестной информации о движении объекта, если известна другая информация. В следующей части Урока 6 мы исследуем этот процесс.
Следующий раздел:
Кинематические уравнения и решение задач
Четыре кинематических уравнения, которые описывают математическую связь между параметрами, описывающими движение объекта, были представлены в предыдущей части Урока 6. Четыре кинематических уравнения:
В приведенных выше уравнениях символ d обозначает перемещение предмет. Символ t обозначает время, в течение которого объект перемещался. Символ a обозначает ускорение объекта. А символ v обозначает мгновенную скорость объекта; индекс i после v (как в v i ) указывает, что значение скорости является начальным значением скорости, а нижний индекс f (как в v f ) указывает, что значение скорости является конечным значением скорости.
Стратегия решения задач
В этой части урока 6 мы исследуем процесс использования уравнений для определения неизвестной информации о движении объекта. Процесс включает в себя использование стратегии решения проблем, которая будет использоваться на протяжении всего курса. Стратегия включает следующие шаги:
Процесс включает в себя использование стратегии решения проблем, которая будет использоваться на протяжении всего курса. Стратегия включает следующие шаги:
- Построить информативную диаграмму физической ситуации.
- Определите и перечислите данную информацию в переменной форме.
- Определите и перечислите неизвестную информацию в переменной форме.
- Определите и перечислите уравнение, которое будет использоваться для определения неизвестной информации из известной.
- Подставьте известные значения в уравнение и используйте соответствующие алгебраические шаги для поиска неизвестной информации.
- Проверьте свой ответ, чтобы убедиться, что он разумен и математически верен.
Использование этой стратегии решения проблемы при решении следующей задачи моделируется в примерах A и B ниже.
Пример задачи A
Има Торопится приближается к светофору, движущемуся со скоростью +30,0 м/с. Свет загорается желтым, и Има нажимает на тормоза и останавливается. Если ускорение Имы равно -8,00 м/с 2 , то определить перемещение автомобиля в процессе заноса. (Обратите внимание, что направления векторов скорости и ускорения обозначены знаком + и -.)
Если ускорение Имы равно -8,00 м/с 2 , то определить перемещение автомобиля в процессе заноса. (Обратите внимание, что направления векторов скорости и ускорения обозначены знаком + и -.)
Решение этой задачи начинается с построения информативной диаграммы физической ситуации. Это показано ниже. Второй шаг включает идентификацию и перечисление известной информации в переменной форме. Обратите внимание, что значение v f можно вывести равным 0 м/с, поскольку машина Имы останавливается. Начальная скорость (v i ) автомобиля равна +30,0 м/с, так как это скорость в начале движения (занос). А ускорение (а) автомобиля равно — 8,00 м/с 2 . (Всегда обращайте особое внимание на знаки + и — для данных величин.) Следующий шаг стратегии включает перечисление неизвестной (или желаемой) информации в переменной форме. В этом случае задача запрашивает информацию о водоизмещении автомобиля. Итак, d — неизвестная величина. Результаты первых трех шагов представлены в таблице ниже.
| Схема: | Дано: | Найти: |
|---|---|---|
| v i = +30,0 м/с v f = 0 м/с a = — 8,00 м/с 2 | д = ?? |
Следующий шаг стратегии включает определение кинематического уравнения, которое позволит вам определить неизвестную величину. На выбор предлагается четыре кинематических уравнения. В общем, вы всегда будете выбирать уравнение, содержащее три известные и одну неизвестную переменную. В этом конкретном случае три известные переменные и одна неизвестная переменная равны v f , v i , a и d. Таким образом, вы будете искать уравнение, в котором перечислены эти четыре переменные. Проверка четырех приведенных выше уравнений показывает, что уравнение в правом верхнем углу содержит все четыре переменные.
v f 2 = v i 2 + 2 • a • d
Как только уравнение определено и записано, следующий шаг стратегии включает подстановку известных значений в уравнение и использование соответствующих алгебраических шагов для поиска неизвестной информации. Этот шаг показан ниже.
Этот шаг показан ниже.
(0 м/с) 2 = (30,0 м/с) 2 + 2 • (-8,00 м/с 2 ) • d
0 м 2 /с
7 2
7 м 2 /с 2 + (-16,0 м/с 2 ) • d
(16,0 м/с 2 ) • d = 900 м 2 0 0 2 /с 2
(16,0 м /с 2 )*D = 900 м 2 /с 2
D = (900 М 2 /S 2 ) /(16,0 м/с 2 )
d = (900 м 2 /с 2 )/ (16,0 м/с 2 )
d = 56,3 м
Приведенное выше решение показывает, что расстояние 5 6,3 метра автомобиля будет скользить. . (Обратите внимание, что это значение округляется до третьего знака.)
Последний шаг стратегии решения проблем включает проверку ответа, чтобы убедиться, что он является разумным и точным. Стоимость кажется достаточно разумной. Автомобилю требуется значительное расстояние, чтобы занести от 30,0 м / с (примерно 65 миль / ч) до остановки. Рассчитанное расстояние составляет примерно половину футбольного поля, что делает его очень разумным расстоянием для заноса. Проверка точности включает подстановку вычисленного значения обратно в уравнение для смещения и обеспечение того, чтобы левая часть уравнения была равна правой части уравнения. Это действительно так!
Рассчитанное расстояние составляет примерно половину футбольного поля, что делает его очень разумным расстоянием для заноса. Проверка точности включает подстановку вычисленного значения обратно в уравнение для смещения и обеспечение того, чтобы левая часть уравнения была равна правой части уравнения. Это действительно так!
Пример задачи B
Бен Рашин ждет на светофоре. Когда он, наконец, стал зеленым, Бен разогнался из состояния покоя со скоростью 6,00 м/с 2 за время 4,10 секунды. Определите перемещение автомобиля Бена за этот период времени.
Еще раз, решение этой проблемы начинается с построения информативной диаграммы физической ситуации. Это показано ниже. Второй шаг стратегии включает идентификацию и перечисление известной информации в переменной форме. Обратите внимание, что версия 9Можно сделать вывод, что значение 0023 i равно 0 м/с, поскольку изначально автомобиль Бена находится в состоянии покоя. Ускорение (а) автомобиля равно 6,00 м/с 2 . А время (t) равно 4,10 с. Следующий шаг стратегии включает перечисление неизвестной (или желаемой) информации в переменной форме. В этом случае задача запрашивает информацию о водоизмещении автомобиля. Итак, d — неизвестная информация. Результаты первых трех шагов представлены в таблице ниже.
А время (t) равно 4,10 с. Следующий шаг стратегии включает перечисление неизвестной (или желаемой) информации в переменной форме. В этом случае задача запрашивает информацию о водоизмещении автомобиля. Итак, d — неизвестная информация. Результаты первых трех шагов представлены в таблице ниже.
| Диаграмма: | Дано: | Найти: |
|---|---|---|
| v i = 0 м/с t = 4,10 с а = 6,00 м/с 2 | д = ?? |
Следующий шаг стратегии включает определение кинематического уравнения, которое позволит вам определить неизвестную величину. На выбор предлагается четыре кинематических уравнения. Опять же, вы всегда будете искать уравнение, содержащее три известные переменные и одну неизвестную переменную. В этом конкретном случае три известные переменные и одна неизвестная переменная равны t, v и , а и г. Проверка четырех приведенных выше уравнений показывает, что уравнение в левом верхнем углу содержит все четыре переменные.
d = v i • t + ½ • a • t 2
Как только уравнение определено и записано, следующий шаг стратегии включает подстановку известных значений в уравнение и использование соответствующих алгебраических шагов для поиска неизвестной информации. Этот шаг показан ниже.
d = (0 м/с) • (4,1 с) + ½ • (6,00 м/с 2 ) • (4,10 с) 2
d = (0 м) + ½ • (6,00 м/с 2 ) • (16,81 с 2 )
+ 9,04 м3 d0 =
d0
d = 50,4 м
Приведенное выше решение показывает, что автомобиль проедет расстояние 50,4 метра. (Обратите внимание, что это значение округляется до третьего знака.)
Последний шаг стратегии решения проблем включает проверку ответа, чтобы убедиться, что он является разумным и точным. Стоимость кажется достаточно разумной. Автомобиль с ускорением 6,00 м/с/с достигнет скорости примерно 24 м/с (примерно 50 миль/ч) за 4,10 с. Расстояние, на которое такой автомобиль переместится за этот период времени, составит примерно половину футбольного поля, что делает это расстояние вполне разумным.

Всего комментариев: 0