Как устроен вращающийся центр и в каких случаях его применяют: Центр вращающийся токарный|Торцевые захваты, поводковые патроны

Центр вращающийся токарный|Торцевые захваты, поводковые патроны

OSNASTIK

Южная Корея / Индия

• Центра вращающиеся и упорные

  • Вращающиеся задние центры
  • Вращающиеся центры для труб
  • Вращающиеся задние центры со сменными наконечниками
  • Упорные центры, упорные центры для труб

WIDIN

Южная Корея

• Токарные центры WIDIN

  • Вращающиеся центры для токарных станков. Тип LC-NC
  • Вращающиеся центры для токарных станков. Тип LC-NCP
  • Вращающиеся центры для тяжелой обработки. LC-NK NKD
  • Вращающиеся центры для шлифовальной обработки. Тип LC-SMP
  • Вращающиеся центры для высокоскоростной обработки. Тип LC-D50
  • Вращающиеся центры с уплотнениями. Тип LC-HD
  • Вращающиеся конуса. Тип LC-PT
  • Упорные центры. Тип LM и LM-H

Центр вращающийся токарный

Токарные центра вращающиеся (упорные центра) используются в токарных станках. Вращающиеся центра служат для уменьшения радиального биения путём закрепления заготовок. Для закрепления вращающийся центр подводится к незакреплённой стороне заготовки и прижимает её. Таким образом, заготовка оказывается закреплена с обеих сторон: с одной стороны зажимным патроном, с другой стороны — токарным центром. Такое закрепление позволяет работать с большей скоростью и увеличенным нажимом резака.

Представленные в данном разделе вращающиеся центра для токарного станка отличаются различными возможностями и преимуществами:

   По конструкции наконечника:

• Вращающийся наконечник — используется при не вращающейся задней бабке станка для снижения трения между заготовкой и наконечником центра.
• Не вращающийся наконечник — обладает более низкой стоимостью и увеличенной износостойкостью, так как является цельнометаллическим.

   По креплению наконечника:

• Съёмный наконечник — позволяет сменять наконечники вращающегося центра вручную или автоматически (на станках с ЧПУ), что увеличивает универсальность применения центра, а также увеличивает срок службы.
• Несъёмный наконечник — обладает более низкой стоимостью.

   По виду заготовки:

• Цельнометаллическая заготовка — центра со стандартными наконечниками.
• Полые заготовки, трубы и пр. — т.н. «грибковые центра» с увеличенным наконечником, представляющим из себя усечённый конус.

Вращающиеся центры для токарных станков

В данной статье речь пойдет о токарных центрах, об их конструкции, разновидностях и особенностях эксплуатации.

Одна из самых распространенных заготовок обрабатываемых на токарных станках — это валы, причем валы различной длины. Для того чтобы добиться небходимого качества поверхности их нужно достаточно жестко и надежно закрепить. Делается это самым эффективным и проверенным способом — с одной стороны вал зажимается в патрон, а с другой поджимается центром. В большинстве случаев для этого используется вращающийся центр, который устанавливается в пиноль задней бабки.

В каких случаях необходимо использование вращающегося центра:

• 
  Длина заготовки в 5 раз превышает диаметр. 

• 
  Точение тяжелых деталей на высоких скоростях (большие обороты и подача).  

• 
  Большая толщина снимаемой стружки. 

• 
  Когда чистовая обработка будет проходить на шлифовальном станке. 

Преимущества использования центров:

• 
  Длительный срок эксплуатации. 

• 
  Устойчивость к высоким нагрузкам. 

• 
  Возможность увеличить скорость обработки. 

• 
  Повышение производительности оборудования. 

• 
  Универсальность — можно использовать на станках с ручным управлением, и на оборудовании с ЧПУ. 

• Высокое качество деталей.

Конструкция вращающихся центров

Вращающийся центр состоит из конического наконечника, вала и подшипника, размещенного в стальном корпусе. От подшипника во многом и зависит на каких режимах может работать центр, так же он снижает трение.

При стандартных режимах работы используют центра с углом наконечника 60º, при тяжелых режимах целесообразно применять с углом 90º.

Разновидности

В зависимости от особенностей решаемых задач при токарной обработке центра бывают нескольких типов:

• Упорный центр — применяется при небольших скоростях обработки. Предварительно необходимо сделать центровочное отверстие. 

• Упорный со срезанным конусом — используются при подрезании торца

• Вращающийся — используется при высоких скоростях обработки, где упорный уже нельзя применить.

• Грибковый — имеет наконечник с усеченным конусом. Используется для фиксации деталей с внутренним отверстием (трубы, полые валы). 

• С вращающейся гайкой — для удобства извлечения из задней бабки

• Со сменными наконечниками — возможность обработки широкого спектра деталей, используя всего один центр

Центры для токарных станков изготавливаются из высокопрочной легированной стали. В зависимости от сложности процесса они бывают обычные и усиленные. Последние используются при работе с тяжелыми изделиями. Усиленный отличается прочностью и устойчивостью к высоким нагрузкам.

Специфика эксплуатации

Перед началом работы токарю необходимо учесть погрешности биения. Оно возникает из-за износа подшипников или наконечника, недостаточно жесткой фиксации. Если требования не допускают такую погрешность, лучше воспользоваться другой оснасткой.


Какие нюансы нужно учесть при обработке в центрах:

• 
  Оси шпинделя и центра должны совпадать, иначе будут погрешности в обработке. При точении деталей с высоким классом точности нужно оставлять припуски для чистовой обработки. 

• 
  Сила зажима должна надежно фиксировать заготовку, но при этом не мешать ее вращению.


Важно!


Биение вращающегося центра приводит к радиальному биению детали относительно оси. Дальнейшая обработка этой же заготовки на другом станке может привести к нарушению соосности.


При обнаружении сильного биения конический наконечник необходимо отшлифовать специальным инструментом, который крепится в резцедержателе. После проверки шаблоном в случае удовлетворительного результата можно приступать к металлообработке.


Важно!


При точении на больших оборотах изнашивается наконечник центра и разбивается центровочное отверстие. Чтобы продлить срок эксплуатации оснастки, наконечник обрабатывают защитной смазкой.

---


Источники:


1) каталог Bison-Bial 2015


2) https://vseostankah.com/tokarnye-stanki/vrashhayushhijsya-tsentr-nepodvizhnyj-gribkovyj.html


3) https://mekkain.ru/library/czentr-upornyij.html

---


Каталог станочной оснастки на онлайн-выставке Enex: https://enex.market/catalog/stanki_i_komplektuyushchie_k_nim/stanochnaya_osnastka/.

Правила вращения — обзор геометрии (видео)

TranscriptPractice

Привет и добро пожаловать в это видео о вращении! В этом видео мы рассмотрим вращение фигуры вокруг точки. Давайте узнаем о ротациях!

Вращения везде, куда ни глянь. Земля — наиболее распространенный пример, вращающийся вокруг оси. Колесо автомобиля или велосипеда вращается вокруг центрального болта. Эти два примера вращаются на 360°. Существуют и другие формы вращения, которые меньше, чем полное вращение на 360 °, например, персонаж или объект, вращающийся в видеоигре. Говоря более формально, вращение — это форма преобразования, при котором фигура поворачивается вокруг точки. Мы называем эту точку центр вращения . Фигура и ее вращение сохраняют ту же форму и размер, но смотрят в другом направлении. Фигуру можно вращать по часовой или против часовой стрелки. Еще один отличный пример вращения в реальной жизни — колесо обозрения, центральная ступица которого является центром вращения.

Мера, на которую фигура поворачивается вокруг центра вращения, называется углом поворота . Угол поворота обычно измеряется в градусах. Указываем градусную меру и направление вращения. Вот фигура повернута на 90° по часовой стрелке и против часовой стрелки относительно центральной точки.

Отличный математический инструмент, который мы используем для отображения поворотов, — это координатная сетка. Давайте начнем с вращения точки вокруг центра (0,0). Если вы возьмете координатную сетку и нанесете точку, а затем повернете бумагу на 90° или 180° по часовой стрелке или против часовой стрелки вокруг начала координат, вы сможете найти положение повернутой точки. Давайте посмотрим на реальный пример, здесь мы нанесли точку A в (5,6), затем повернули бумагу на 90° по часовой стрелке, чтобы создать точку A’, которая находится в (6,-5).

Вот та же точка A в (5,6), повернутая на 180° против часовой стрелки вокруг начала координат, чтобы получить A’(-5,-6).

Давайте подробнее рассмотрим два вращения из нашего эксперимента. В нашем первом эксперименте, когда мы поворачивали точку A (5,6) на 90° по часовой стрелке вокруг начала координат, чтобы создать точку A’ (6,-5), значение y точки A стало значением x точки A’ и значение x точки A стало значением y точки A’, но с противоположным знаком.

В нашем втором эксперименте точка A (5,6) поворачивается на 180° против часовой стрелки вокруг начала координат, создавая точку A’ (-5,-6), где значения x и y такие же, как у точки A, но с противоположные знаки.

К счастью для нас, эти эксперименты позволили математикам разработать правила для наиболее распространенных поворотов на координатной сетке, приняв начало координат (0,0) за центр вращения. Вот правила вращения :

• Вращение на 90° по часовой стрелке: (x,y) становится (y,-x)
• Вращение на 90° против часовой стрелки: (x,y) становится (-y,x)
• 180 ° вращение по и против часовой стрелки: (x, y) становится (-x,-y)
• вращение на 270° по часовой стрелке: (x,y) становится (-y,x)
• Вращение на 270° против часовой стрелки: (x,y) становится (y,-x)

Как видите, два наших эксперимента следуют этим правилам.

Примеры вращения

Теперь, когда мы знаем, как вращать точку, давайте рассмотрим вращение фигуры на координатной сетке. Чтобы повернуть треугольник ABC вокруг начала координат на 90° по часовой стрелке, мы должны следовать правилу (x,y) → (y,-x), где значение y исходной точки становится новым значением x, а значение x исходной точки исходная точка становится новым значением y с противоположным знаком. Давайте применим правило к вершинам, чтобы создать новый треугольник A’B’C’:

• A (-4, 7) становится A’ (7, 4)
• B (-6, 1) становится B’ (1, 6)
• C (-2, 1) становится C’ (1, 6) 2)

Давайте посмотрим на другую ротацию. Повернем треугольник ABC на 180° вокруг начала координат против часовой стрелки, хотя при вращении фигуры на 180° по часовой стрелке и против часовой стрелки используется то же правило, что (x,y) становится (-x,-y), где координаты вершин повернутый треугольник — это координаты исходного треугольника с противоположным знаком. Давайте применим правило к вершинам, чтобы создать новый треугольник A’B’C’:

• A (2,7) становится A’ (-2,-7)
• B (2,1) становится B’ (-2,-1)
• C (6,1) становится C’ (- 6,-1)

Вот четырехугольник ABCD. Чтобы повернуть четырехугольник ABCD на 90° против часовой стрелки вокруг начала координат, мы воспользуемся правилом (x,y) превращается в (-y,x). Давайте применим правила к вершинам, чтобы создать четырехугольник A’B’C’D’:

• A (-8,-2) становится A’ (2,-8)
• B (-7,-7) становится B’ (7,-7)
• C (-2,-6) становится C’ (6,-2)
• D (-3,-2) становится D’ (2,-3)

Теперь я хочу, чтобы вы сами попробовали несколько практических задач. Воздушный змей KLMN показан на координатной сетке. Воздушный змей был повернут вокруг исходной точки, чтобы создать воздушный змей K’L’M’N’. Можете ли вы определить, какое вращение воздушного змея KLMN создало воздушный змей K’L’M’N’?

Начнем с определения координат вершин воздушного змея KLMN и нашего повернутого воздушного змея:

• K (-8,3) становится K’ (8,-3)
• L (-5,5) становится L ‘(5,-5)
• М (-2,3) становится М’ (2,-3)
• N (-5,-3) становится N’ (5,3)

Более пристальный взгляд на координаты вершин показывает, что координаты K’L’M’N’ совпадают с координатами вершин оригинальный воздушный змей, но с обратным знаком. Давайте посмотрим на правила, единственное правило, при котором значения x и y не меняются, но меняется их знак, — это поворот на 180°.

• Вращение на 90° по часовой стрелке: (x,y) становится (y,-x)
• Вращение на 90° против часовой стрелки: (x,y) становится (-y,x)
• Вращение на 180° по часовой и против часовой стрелки: (x ,y) становится (-x,-y)
• Вращение на 270° по часовой стрелке: (x,y) становится (-y,x)
• Вращение на 270° против часовой стрелки: (x,y) становится (y,-x)

Таким образом, воздушный змей KLMN был повернут на 180° вокруг происхождение для создания воздушного змея K’L’M’N’.

Давайте рассмотрим другую задачу. Пентагон QRSTU показан на координатной сетке. Поверните пятиугольник QRSTU на 90° против часовой стрелки, чтобы создать пятиугольник Q’R’S’T’U’.

Начнем с определения координат вершин нашего исходного пятиугольника. Правило для поворота на 90° против часовой стрелки: (x,y) становится (-y,x), давайте применим правило, чтобы найти вершины нашего нового пятиугольника.

(x,y) становится (-y,x)

• Q (-6,6) становится Q’ (-6,-6)
• R (-4,7) становится R’ (-7, -4)
• S (0,4) становится S’ (-4,0)
• T (-4,1) становится T’ (-1,-4)
• U (-6,2) становится U ‘ (-2,-6)

Теперь давайте нанесем точки на координатную сетку и пометим вершины.

Последнее практическое задание. Трапеция PQRS, где P (-3,-5), Q (3,-5), R (5,-2) и S (-5,-2) повернута на 90 ° по часовой стрелке вокруг начала координат для создания трапеции P ‘Вопросы’. Создайте обе трапеции на координатной сетке.

Мы начнем с решения, какое правило использовать для поворота на 90° по часовой стрелке вокруг начала координат. Мы собираемся использовать (x,y) в (y,-x). Теперь применим правило к координатам вершин PQRS.

• P (-3,-5) становится P’ (-5,3)
• Q (3,-5) становится Q’ (-5,-3)
• R (5,-2) становится R ‘ (-2,-5)
• S (-5,-2) становится S’ (-2,5)

Теперь давайте нанесем точки и создадим трапеции на координатной сетке.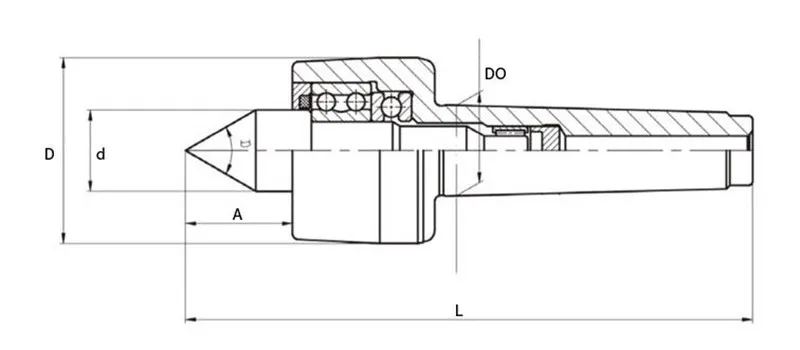

Надеюсь, этот обзор ротации был полезен! Спасибо за просмотр и удачной учебы!

Практические вопросы

Вопрос №1:

 
На координатной плоскости точка A \((3,-4)\) поворачивается на 180° против часовой стрелки вокруг начала координат, образуя повернутую точку \( А’\). Что из следующего является упорядоченной парой для \(A’\)?

\((4,-3)\)

\((-3,-4)\)

\((-3,4)\)

\((-4,3)\)

Показать ответ

Ответ:

Поворот точки с координатами \((x,y)\) на 180° вокруг начала координат против или по часовой стрелке дает точку с координатами \((-x ,-у)\). Подставляя координаты точки \(A\) в нашу формулу для нахождения повернутой точки, мы получаем:

\(A’\влево(-3,-\влево(-4\вправо)\вправо)=A'(-3,\ 4)\)

Скрыть ответ

Вопрос №2:

Координаты вершин треугольника ABC, которые можно изобразить на координатной плоскости, равны \(A(-8,-6)\), \(B(-2,-6)\) и \(C(- 5,-3)\). Треугольник поворачивается на 90° по часовой стрелке вокруг начала координат, образуя треугольник \(A’B’C’\). Какие из следующих вершин являются вершинами треугольника \(A’B’C’\)?

\(A’\влево(6,-8\вправо),B’\влево(6,-2\вправо), C’(3,-5)\)

\(A’\влево(-6,\8\вправо), B’\влево(-6,2\вправо), C'(-3,\ 5)\)

\(A’\влево (-8,\ 6\право), B’\лево(-6,\ 2\право), C'(5,\ -3)\)

\(A’\лево(8,\ 6\право) ), B’\left(2,\ 6\right), C'(-5,\ -3)\)

Показать ответ

Ответ:

Вращение точки с координатами \((x ,y)\) 90° вокруг начала координат по часовой стрелке дает точку с координатами \((y,-x)\). Подставляя координаты наших точек в нашу формулу для нахождения повернутых точек, мы получаем:

\(A’\влево(-6,-\влево(-8\вправо)\вправо)=A’\влево(-6,\8\вправо)\)
\(B’\влево(-6 ,-\влево(-2\вправо)\вправо)=B’\влево(-6,\ 2\вправо)\)
\(C’\влево(-3,-\влево(-5\вправо)\ right)=C'(-3,\ 5)\)

Таким образом, координаты вершин треугольника \(A’B’C’ равны A’\left(-6,\ 8\right)\), \(B’\влево(-6,\2\вправо)\) и \(C'(-3,\5)\).

Скрыть ответ

Вопрос №3:

 
График четырехугольника ABCD показан ниже.

Четырехугольник поворачивается на 270° против часовой стрелки вокруг начала координат, образуя четырехугольник \(A\простой B\простой C\простой D\простой\). Что из следующего является графиком четырехугольника \(A\простое число B\простое число C\простое число D\простое число\)?

Показать ответ

Ответ:

Поворот точки с координатами \((x,y)\) на 270° вокруг начала координат в направлении против часовой стрелки дает точку с координатами \((y,- Икс)\). Подставляя координаты вершин четырехугольника \(ABCD\) в нашу формулу для нахождения повернутых вершин четырехугольника \(A\простое число B\простое число C\простое число D\простое число\), мы получаем:

\(A\простое число\). \left(4,-8\right)\ B\prime\left(7,-8\right)\ C\prime\left(8,-2\right)\ D\prime\left(2,\-2 \справа)\)

График четырех повернутых точек показан на координатной плоскости ниже.

Соединив последовательно вершины из \(A\prime\) в \(D\prime\) отрезками из четырех прямых, получим график четырехугольника \(A\prime B\prime C\prime D\prime\) показано ниже.

Скрыть ответ

Вопрос № 4:

 
Часы наложены на координатную плоскость так, что их центр находится в начале координат, как показано ниже.

Часы показывают 12:10. Сколько будет времени, если минутную стрелку повернуть на 180° вокруг начала координат по часовой стрелке?

12:40

12:25

11:40

11:55

Показать ответ

Ответ:

900 \) 180° вокруг начала координат по часовой стрелке или против часовой стрелки дает точку с координатами \((-x,-y)\). Хотя конец минутной стрелки часов не лежит в точке \((7,4)\), там находится время, которое она представляет в минутах. Подставив координаты этой точки в нашу формулу для нахождения повернутой точки, мы получим \(\left(-7,-4\right)\).

Вращая минутную стрелку часов в направлении повернутой точки, мы можем узнать, который сейчас час.

Каждое числовое значение на часах соответствует 5 минутам для минутной стрелки и 1 часу для часовой стрелки. Поскольку повернутая точка лежит на цифре 8 часов, показание минутной стрелки равно 40 минутам. Поскольку вращение происходит по часовой стрелке, часовая стрелка также вращается по часовой стрелке, чтобы представить время позже 12:10, правильное время после вращения минутной стрелки — 12:40.

Скрыть ответ

Вопрос №5:

 
Водяное колесо имеет диаметр 20 футов. Вода из поилки, расположенной над водяным колесом, выливается на лопасти водяного колеса, заставляя его вращаться по часовой стрелке. Вода в весле начинает вытекать из водяного колеса после того, как оно повернется на 90°. Если вода попадает в весло в точке, показанной на графике на координатной плоскости ниже, каковы координаты точки, в которой вода выходит из водяного колеса? Центр водяного колеса находится в начале координатной плоскости.

\((3,9)\)

\((-3,-9)\)

\((-9,-3)\)

\((9,-3)\)

Показать ответ

Ответ:

Поворот точки с координатами \((x,y)\) на 90° вокруг начала координат по часовой стрелке дает точку с координатами \((y,-x )\). Подставив координаты точки, где вода входит в весло, в нашу формулу, мы получим нашу повернутую точку \((9,-3)\). Таким образом, координаты точки сброса воды из водяного колеса равны \((9,-3)\).

Обратите внимание, что в повернутой точке координатной плоскости вода из весла начинает вытекать из водяного колеса.

Скрыть ответ

 

Вернуться к видео о геометрии

602600

Найти центр вращения

При всех вращениях есть одна фиксированная точка, называемая 9029.9 центр вращения — вокруг которого вращается все остальное.

Эта точка может находиться внутри фигуры, в этом случае фигурка остается на месте и просто вращается. Или точка может быть за пределами фигуры, и в этом случае фигура движется по дуге окружности (подобно орбите) вокруг центра вращения. Величина поворота называется углом поворота .

Самый простой способ понять это — решить задачу: На следующем рисунке треугольник-прообраз ABC был повернут для создания треугольника изображения 9.0299 А’Б’С’ . Найдите центр вращения.

Для начала возьмите три отрезка, которые соединяют точки прообраза с точками их изображения (в данном случае линия AA’ , линия BB’, и линия CC’ ). При всех вращениях центр вращения лежит на пересечении серединных перпендикуляров таких отрезков. Поскольку три серединных перпендикуляра пересекаются в одной точке, вам нужно всего два из них, чтобы найти точку пересечения. Подойдут любые две, поэтому найдите серединные перпендикуляры прямых 9.0299 АА’ и ВВ’ ; затем вы можете установить их уравнения равными друг другу, чтобы найти, где они пересекаются.

Сначала найдите середину прямой AA’ :

Затем найдите наклон прямой AA’ :

9/2, а именно 2/9. Таким образом, форма точки-наклона для серединного перпендикуляра равна

. Выполните тот же процесс, чтобы получить серединный перпендикуляр к линии 9.0299 BB’ :

Наклон биссектрисы, перпендикулярной линии BB’ , обратно пропорционален -9/5, что равно 5/9. Таким образом, уравнение биссектрисы равно

Теперь, чтобы найти, где пересекаются две перпендикулярные биссектрисы, приравняйте правые части их уравнений и решите для x :

Умножьте обе части на 9 избавиться от дробей; затем разделите:

Подставьте –10 обратно в любое уравнение, чтобы получить y :

Вы сделали это. Центр вращения

Дайте этой точке имя — как насчет точки Z ?

На следующем рисунке показаны точка Z , угол AZA’ и небольшая стрелка против часовой стрелки, которая указывает вращательное движение, которое переместит треугольник ABC в треугольник A’B’C’.