Как устроен вращающийся центр и в каких случаях его применяют: Центр вращающийся токарный|Торцевые захваты, поводковые патроны
Содержание
Центр вращающийся токарный|Торцевые захваты, поводковые патроны
OSNASTIK
Южная Корея / Индия
Центра вращающиеся и упорные
- Вращающиеся задние центры
- Вращающиеся центры для труб
- Вращающиеся задние центры со сменными наконечниками
- Упорные центры, упорные центры для труб
WIDIN
Южная Корея
Токарные центры WIDIN
- Вращающиеся центры для токарных станков.
 Тип LC-NC
Тип LC-NC - Вращающиеся центры для токарных станков. Тип LC-NCP
- Вращающиеся центры для тяжелой обработки. LC-NK NKD
- Вращающиеся центры для шлифовальной обработки. Тип LC-SMP
- Вращающиеся центры для высокоскоростной обработки. Тип LC-D50
- Вращающиеся центры с уплотнениями.
 Тип LC-HD
Тип LC-HD - Вращающиеся конуса. Тип LC-PT
- Упорные центры. Тип LM и LM-H
- Вращающиеся центры для токарных станков.
Центр вращающийся токарный
Токарные центра вращающиеся (упорные центра) используются в токарных станках. Вращающиеся центра служат для уменьшения радиального биения путём закрепления заготовок. Для закрепления вращающийся центр подводится к незакреплённой стороне заготовки и прижимает её. Таким образом, заготовка оказывается закреплена с обеих сторон: с одной стороны зажимным патроном, с другой стороны — токарным центром. Такое закрепление позволяет работать с большей скоростью и увеличенным нажимом резака.
Такое закрепление позволяет работать с большей скоростью и увеличенным нажимом резака.
Представленные в данном разделе вращающиеся центра для токарного станка отличаются различными возможностями и преимуществами:
По конструкции наконечника:
- Вращающийся наконечник — используется при не вращающейся задней бабке станка для снижения трения между заготовкой и наконечником центра.
- Не вращающийся наконечник — обладает более низкой стоимостью и увеличенной износостойкостью, так как является цельнометаллическим.
По креплению наконечника:
- Съёмный наконечник — позволяет сменять наконечники вращающегося центра вручную или автоматически (на станках с ЧПУ), что увеличивает универсальность применения центра, а также увеличивает срок службы.
- Несъёмный наконечник — обладает более низкой стоимостью.
По виду заготовки:
- Цельнометаллическая заготовка — центра со стандартными наконечниками.
- Полые заготовки, трубы и пр.
 — т.н. «грибковые центра» с увеличенным наконечником, представляющим из себя усечённый конус.
— т.н. «грибковые центра» с увеличенным наконечником, представляющим из себя усечённый конус.
Центр вращающийся — конструкция, применение, виды, ГОСТы
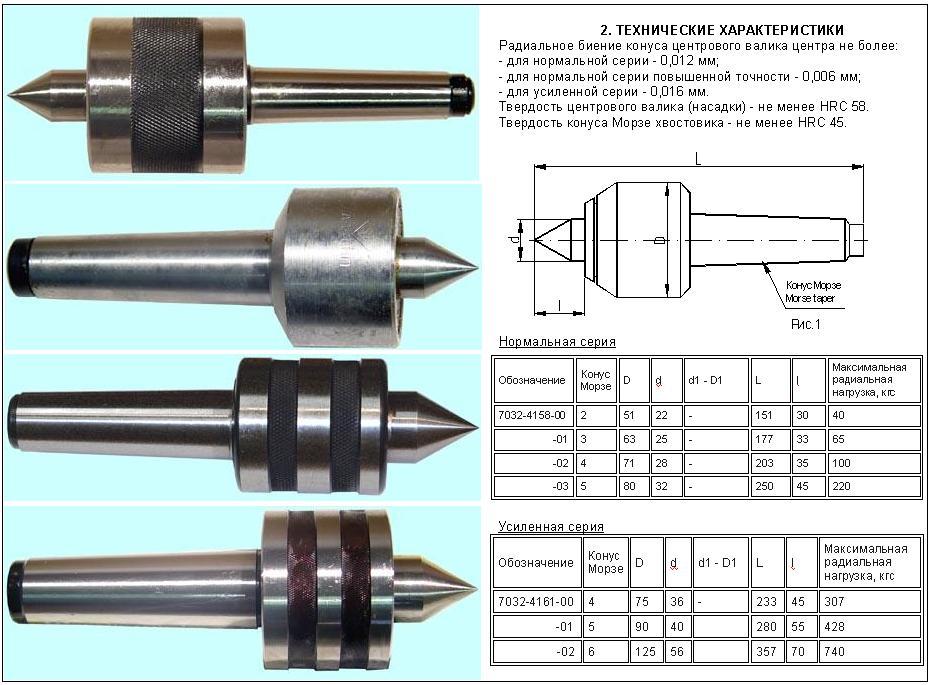
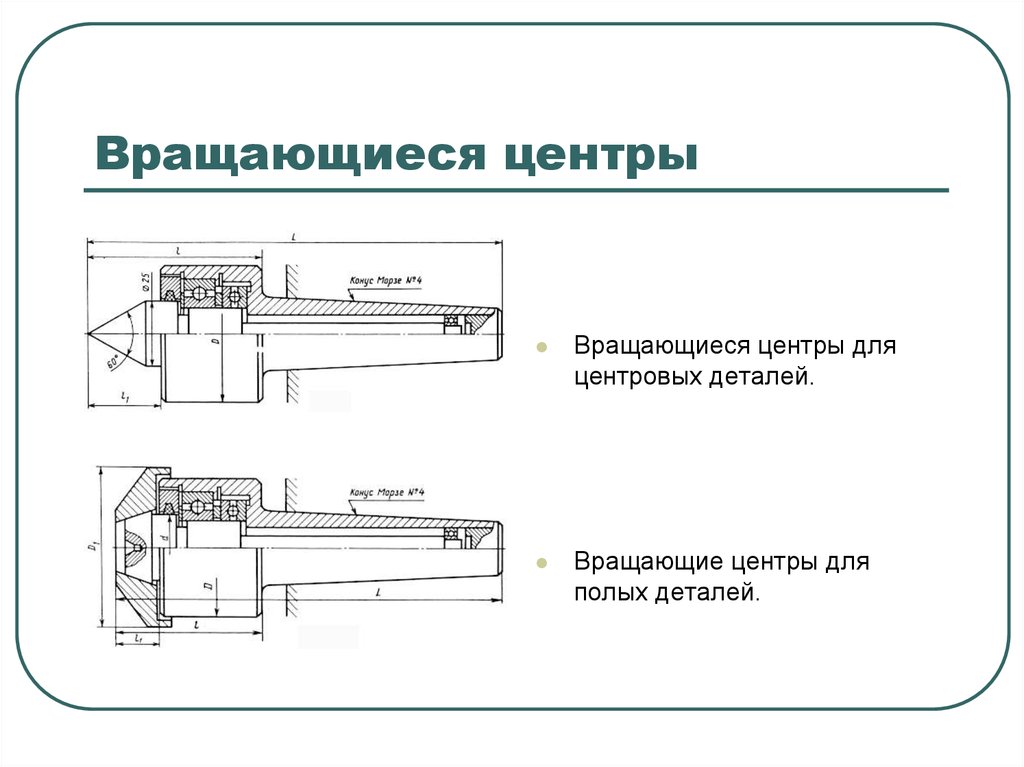
На рисунке выше изображена конструкция центра предназначенного для фиксации в конический паз пиноли задней бабки токарного станка. Рабочая часть или центр (1) вращается благодаря шариковым подшипникам (2) и (4), в других вариантах конструкции применяются игольчатые подшипники. Возникающее в процессе работы осевое давление компенсирует упорный шариковый подшипник (5). Крепление в пиноли обеспечивает конический хвостовик (3). Для точного определения осевых усилий некоторые конструкции имеют встроенный прибор.
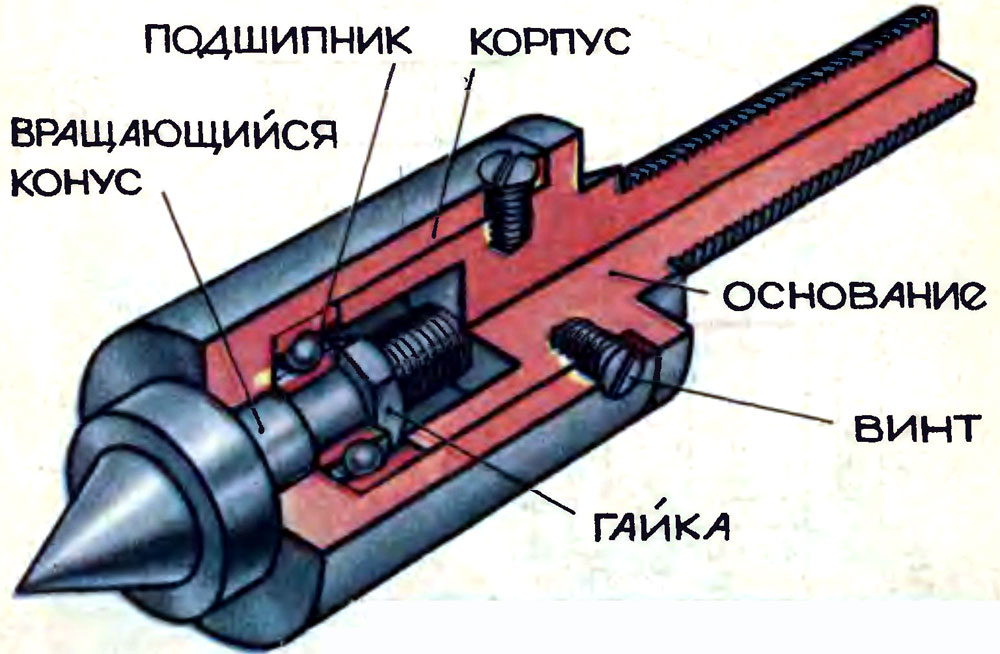
Более надежную фиксацию заготовок, особенно при работе с тяжелыми деталями на больших скоростях, обеспечивают встроенные в пиноль центры. Данное конструктивное исполнение, приведенное на рисунке ниже, даёт более высокую жесткость фиксации, оптимально при подготовке стружек большого сечения.
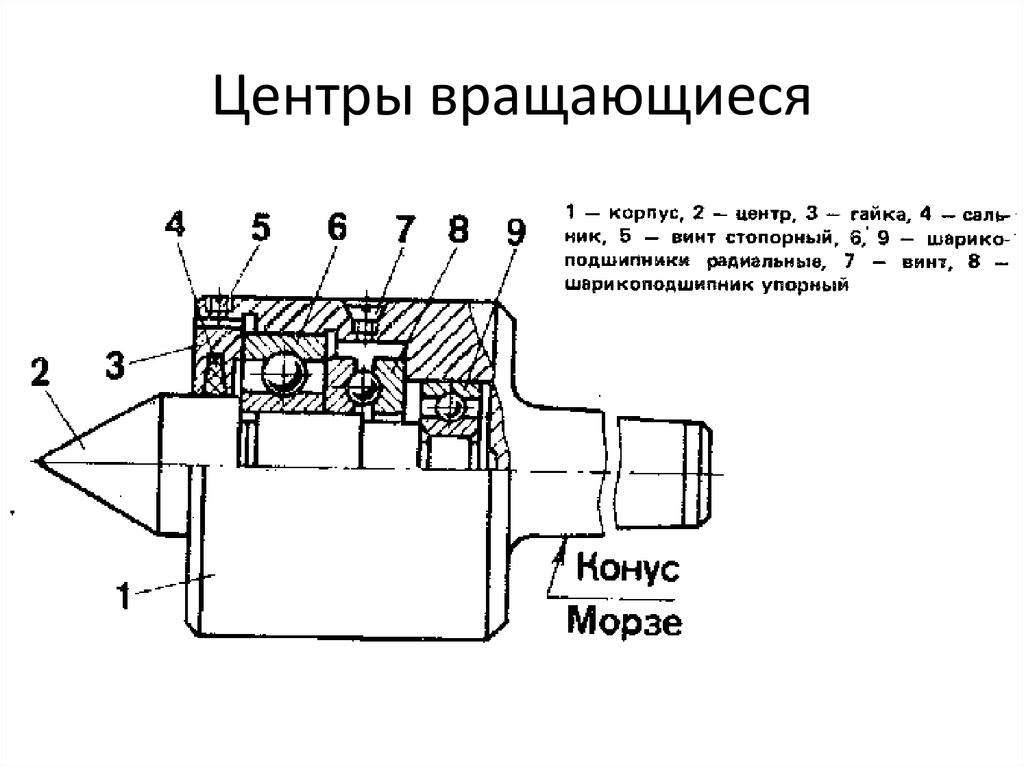
В передней части пиноли (1) имеется специально расточенное отверстие. В нем установлены подшипники для втулки (4) – упорный (3) расположенный в передней части для восприятия осевой нагрузки и радиальный (2). Во втулке выточено коническое отверстие под центр (5). Данную конструкцию можно использовать для крепления сверла или любого другого осевого инструмента, для чего втулка соединяется стопором с пинолью.
В нем установлены подшипники для втулки (4) – упорный (3) расположенный в передней части для восприятия осевой нагрузки и радиальный (2). Во втулке выточено коническое отверстие под центр (5). Данную конструкцию можно использовать для крепления сверла или любого другого осевого инструмента, для чего втулка соединяется стопором с пинолью.
Вращающийся центр для токарного станка своими руками
Многие домашние мастера задумываются о том, как самостоятельно изготовить токарный станок по металлу.
Такое желание объясняется тем, что при помощи подобного устройства, стоить которое будет совсем недорого, можно эффективно выполнять большой перечень токарных операций, придавая заготовкам из металла требуемые размеры и форму.
Казалось бы, намного легче приобрести простейший настольный станок и использовать его в своей мастерской, но учитывая немалую стоимость такого оборудования, есть смысл потратить время на то, чтобы сделать его своими руками.
Самодельный токарный станок — это вполне реально
Использование токарного станка
Токарный станок, который одним из первых появился в линейке оборудования для обработки деталей из разных материалов, в том числе из металла, позволяет изготавливать изделия различных форм и размеров.
С помощью такого агрегата можно выполнять обточку наружных и внутренних поверхностей заготовки, высверливать отверстия и растачивать их до требуемого размера, нарезать наружную или внутреннюю резьбу, выполнять накатку с целью придания поверхности изделия желаемого рельефа.
Серийный токарный станок по металлу — это габаритное устройство, управлять которым не так просто, а его стоимость очень сложно назвать доступной.
Использовать такой агрегат в качестве настольного оборудования нелегко, поэтому есть смысл сделать токарный станок для своей домашней мастерской самостоятельно.
Используя такой мини-станок, можно оперативно производить обточку заготовок, выполненных не только из металла, но также из пластика и древесины.
На таком оборудовании обрабатываются детали, имеющие круглое сечение: оси, рукоятки инструментов, колеса, конструктивные элементы мебели и изделия любого другого назначения.
В подобных устройствах заготовка располагается в горизонтальной плоскости, при этом ей придается вращение, а излишки материала снимает резец, надежно зафиксированный в суппорте станка.
Проточка тормозного диска на самодельном токарном станке
Несмотря на простоту своей конструкции, такой агрегат требует четкой согласованности движений всех рабочих органов, чтобы обработка выполнялась с предельной точностью и наилучшим качеством исполнения.
Пример самодельного токарного станка с чертежами
Рассмотрим подробнее один из рабочих вариантов собранного собственными силами токарного станка, довольно высокое качество которого по праву заслуживает самого пристального внимания. Автор данной самоделки даже не поскупился на чертежи, по которым данное устройство и было успешно изготовлено.
Конечно, далеко не всем требуется настолько основательный подход к делу, зачастую для домашних нужд строятся более простые конструкции, но в качестве донора для хороших идей данный станок подходит как нельзя лучше.
Токарный станок, сделанный своими руками
Внешний вид станка Основные узлы Суппорт, резцедержатель и патрон Вид сбоку Задняя бабка Вид снизу на заднюю бабку Направляющие валы Конструкция суппорта Привод от двигателя
Чертеж №1 Чертеж №2 Чертеж №3
Конструкционные узлы
Любой, в том числе и самодельный, токарный станок состоит из следующих конструктивных элементов: несущей рамы — станины, двух центров — ведущего и ведомого, двух бабок — передней и задней, шпинделя, суппорта, приводного агрегата — электрического двигателя.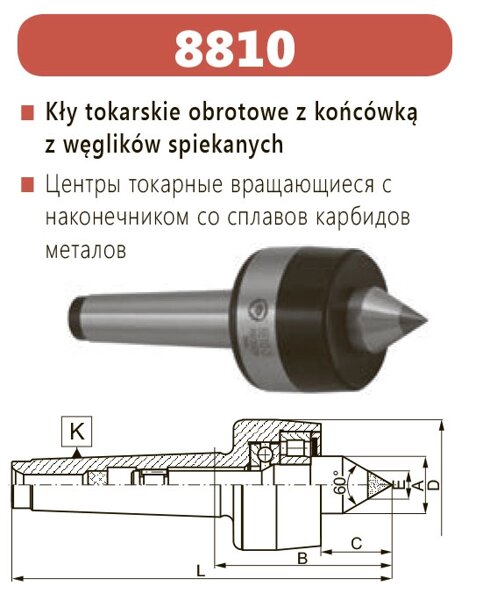
Конструкция малогабаритного токарного станка про металлу
На станине размещают все элементы устройства, она является основным несущим элементом токарного станка.
Передняя бабка — это неподвижный элемент конструкции, на котором располагается вращающийся шпиндель агрегата.
В передней части рамы находится передаточный механизм станка, с помощью которого его вращающиеся элементы связаны с электродвигателем.
Именно благодаря такому передаточному механизму вращение получает обрабатываемая заготовка.
Задняя бабка, в отличие от передней, может перемещаться параллельно направлению обработки, с ее помощью фиксируют свободный конец обрабатываемой заготовки.
Простая схема узлов самодельного станка по дереву подскажет простой вариант изготовления станины, передней и задней бабок
Самодельный токарный станок по металлу можно оснастить любым электродвигателем даже не слишком высокой мощности, но такой двигатель может перегреться при обработке крупногабаритных заготовок, что приведет к его остановке и, возможно, выходу из строя.
Обычно на самодельный токарный станок устанавливают электродвигатели, мощность которых находится в пределах 800–1500 Вт. Даже если такой электродвигатель отличается небольшим количеством оборотов, проблему решают при помощи выбора соответствующего передаточного механизма.
Для передачи крутящего момента от таких электродвигателей обычно используют ременные передачи, очень редко применяются фрикционные или цепные механизмы.
Токарные мини-станки, которыми оснащаются домашние мастерские, могут даже не иметь в своей конструкции такого передаточного механизма: вращающийся патрон агрегата фиксируется непосредственно на валу электродвигателя.
Станок с прямым приводом
Кроме того, необходимо обеспечить надежную фиксацию детали, что особенно важно для моделей лобового типа: с одним ведущим центром.
Решается вопрос такой фиксации при помощи кулачкового патрона или планшайбы.
По сути, токарный станок своими руками можно сделать и с деревянной рамой, но, как правило, для этих целей применяют профили из металла.
Высокая жесткость рамы токарного станка обязательна для того, чтобы на точность расположения ведущего и ведомого центра не оказывали влияние механические нагрузки, а его задняя бабка и суппорт с инструментом беспрепятственно перемещались вдоль оси агрегата.
Использование швеллеров при изготовлении рамы и передней бабки станка
Собирая токарный станок по металлу, важно обеспечить надежную фиксацию всех его элементов, обязательно учитывая нагрузки, которым они будут подвергаться в ходе работы.
На то, какие габариты окажутся у вашего мини-станка, и из каких конструктивных элементов он будет состоять, станет оказывать влияние и назначение оборудования, а также размеры и форма заготовок, которые на нем планируется обрабатывать. От этих параметров, а также от величины планируемой нагрузки на агрегат будет зависеть и мощность электродвигателя, который вам необходимо будет использовать в качестве привода.
Вариант исполнения станины, передней бабки и привода
Для оснащения токарных станков по металлу не рекомендуется выбирать коллекторные электродвигатели, отличающиеся одной характерной особенностью.
Количество оборотов вала таких электродвигателей, а также центробежная сила, которую развивает обрабатываемая заготовка, резко возрастают при уменьшении нагрузки, что может привести к тому, что деталь просто вылетит из патрона и может серьезно травмировать оператора.
Такие электродвигатели допускается использовать в том случае, если на своем мини-станке вы планируете обрабатывать некрупные и нетяжелые детали.
Но даже в таком случае токарный станок необходимо оснастить редуктором, который будет препятствовать бесконтрольному увеличению центробежной силы.
Асинхронный трехфазный электродвигатель, подключаемый к сети 220 Вольт через конденсатор
Уже доказано практикой и конструкторскими расчетами, что для токарных агрегатов, на которых будут обрабатываться заготовки из металла длиной до 70 см и диаметром до 10 см, лучше всего использовать асинхронные электродвигатели мощностью от 800 Вт. Двигатели такого типа характеризуются стабильностью частоты вращения при наличии нагрузки, а при ее снижении в них не происходит ее бесконтрольного увеличения.
Если вы собираетесь самостоятельно сделать мини-станок для выполнения токарных работ по металлу, то обязательно следует учитывать тот факт, что на его патрон будут воздействовать не только поперечные, но и продольные нагрузки. Такие нагрузки, если не предусмотреть ременную передачу, могут стать причиной разрушения подшипников электродвигателя, которые на них не рассчитаны.
Сфера применения и особенности
Центры вращающиеся применяются в токарных станках для обточки деталей при скорости вращения более 75 м/мин. При этой скорости начинается процесс повышенного износа конуса центра и центрового отверстия обрабатываемой заготовки. Частичным путем решения проблемы является применение смазки и твердосплавных напаек, но оптимальным вариант – применение вращающегося центра.
Основные преимущества оснастки:
- Универсальность. При использовании центров со сменной насадкой можно обрабатывать детали с различными конусными осевыми отверстиями.
- Высокие характеристики воспринимаемой нагрузки, значительно превышающие показатели упорных фиксаторов.

- Длительная эксплуатация благодаря уменьшенному износу.
- Возможность работы при высоких показателях нагрузки.
Основным недостатком является наличие радиального биения. Данная проблема решается применение оснастки с допустимым показателем биения, либо финишной обработкой на малых скоростях с использованием неподвижного центра.
Виды вращающихся центров
В зависимости от формы фиксирующей части выпускается два типа вращающихся центров:
- с рабочим конусом для крепления заготовок с центровыми отверстиями;
- с грибообразной насадкой для заготовок с внутренним отверстием – труб, полых валов и т. д.
По конструкции оснастка подразделяется на:
- Центр с постоянным валиком (тип А)
- Центр со сменной насадкой (тип Б)
Конус центрового валика проточен под 60° (исполнение 1) или может иметь дополнительную выточку под конус 30° (исп. 2).
Условное обозначение оснастки: Центр А-1-4-НП ГОСТ 8742-75
Тип А, исполнение 1 с конусом Морзе 4 повышенной точности и нормальной серии.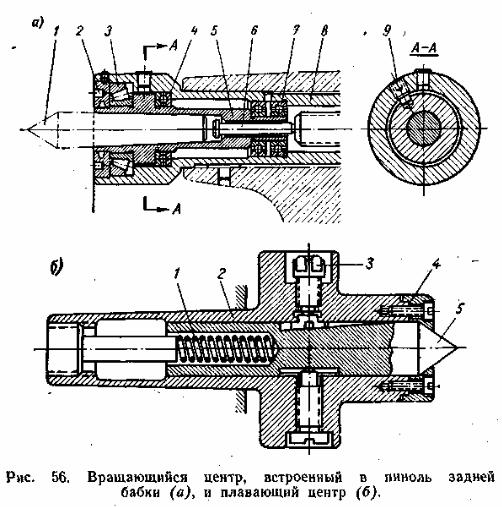
Таблица основных параметров оснастки
| Центры вращающиеся станочные ГОСТ 8742-75 Тип А — с постоянным центровым валиком Тип Б — с насадкой на центровой валик | ||||||||||
| Центр вращающийся тип-исполнение-конус морзе-серия | d | D | L 1 рядL 2 ряд | L 1 рядL 2 ряд | D1 | l1 | ||||
| Центр вращающийся А-1-2-Н | Центр вращающийся А-2-2-Н | Центр вращающийся Б-2-Н | 22 | 56 | 160 | 90 | 56 | 24 | ||
| Центр вращающийся А-1-3-Н | Центр вращающийся А-2-3-Н | Центр вращающийся Б-3-Н | 25 | 63 | 180 | 185 | 94 | 99 | 63 | 26 |
| Центр вращающийся А-1-4-Н | Центр вращающийся А-2-4-Н | Центр вращающийся Б-4-Н | 28 | 71 | 210 | 225 | 101 | 116 | 71 | 30 |
| Центр вращающийся А-1-5-Н | Центр вращающийся А-2-5-Н | Центр вращающийся Б-5-Н | 32 | 80 | 240 | 260 | 104 | 124 | 80 | 34 |
| Центр вращающийся А-1-4-У | Центр вращающийся А-2-4-У | Центр вращающийся Б-4-У | 36 | 75 | 220 | 235 | 111 | 126 | 75 | 36 |
| Центр вращающийся А-1-5-У | Центр вращающийся А-2-5-У | Центр вращающийся Б-5-У | 40 | 90 | 250 | 275 | 114 | 139 | 90 | 45 |
| Центр вращающийся А-1-6-У | Центр вращающийся А-2-6-У | Центр вращающийся Б-6-У | 56 | 125 | 340 | 360 | 150 | 170 | 125 | 56 |
Классификация
В зависимости от материала рабочей части центры подразделяются на два исполнения:
- Исполнение 1 – закаленный конус.

- Исполнение 2 – конус из твердых сплавов.
Неподвижный центр может быть с полным конусом или со срезанным, половиной рабочей части. Последние используются при подрезании торцов, когда резцом необходимо дойти почти до оси вращения обрабатываемой детали.
В зависимости от формы фиксирующей части неподвижные центры подразделяются на оснастку:
- с рабочим конусом для фиксации деталей с центрами и без сквозных или глухих продольных отверстий;
- с грибообразной насадкой для фиксации деталей с внутренним отверстием – труб, полых валов и т. д.;
- Упорные центры выпускаются с отжимной гайкой или без неё. Наличие гайки необходимо в тех случаях, когда на центр действует высокая осевая нагрузка. Применение отжимной гайки позволяет извлечь центр из пиноли без приложения больших усилий.
Особенности эксплуатации
Приведём основные правила эксплуатации вращающихся центров, необходимые для точной обработки деталей:
- При выборе класса точности оснастки необходимо оставить запас на покрытие погрешностей биения вследствие прочих причин – износ подшипников, малая жесткость и т.
 д.
д. - Важную роль играет правильная установка детали. Ось конуса должна с высокой точностью совпадать с осью вращения заготовки.
- Для проверки точности установки можно подложить под вращающийся центр белый лист бумаги и оценить соосность. Более точный контроль производится с помощью индикаторов.
- При наличии биения конус шлифуется по месту с проверкой по шаблону. Обработка осуществляется электроинструментом, расположенным в резцедержателе.
- Биение вращающихся центров приводит к биению полученной детали относительно оси. При установке этой детали на другой станок, имеющий другой показатель биения, может иметь место отклонение от соосности. Для устранения отклонений производится обработка с применением неподвижного центра.
Что такое центробежные и центростремительные силы?
Когда вы покупаете по ссылкам на нашем сайте, мы можем получать партнерскую комиссию. Вот как это работает.
(Изображение предоставлено: Энтони Чинг/Getty Images)
Центростремительные и центробежные силы — это силы, действующие на вращающиеся объекты. Центростремительная сила заставляет объект двигаться по кругу и всегда направлена к центру этого круга. Например, гравитационная сила Солнца является центростремительной силой, удерживающей Земля вращается вокруг нее. Между тем, центробежная сила — это кажущаяся внешняя сила, действующая на объект, который движется по кругу. Примером центробежной силы может быть ощущение, возникающее при езде на карусели, которое заставляет вас лететь наружу.
Центростремительная сила заставляет объект двигаться по кругу и всегда направлена к центру этого круга. Например, гравитационная сила Солнца является центростремительной силой, удерживающей Земля вращается вокруг нее. Между тем, центробежная сила — это кажущаяся внешняя сила, действующая на объект, который движется по кругу. Примером центробежной силы может быть ощущение, возникающее при езде на карусели, которое заставляет вас лететь наружу.
Разница между центростремительной и центробежной силами
Основное различие между центростремительной и центробежной силами заключается в том, что центростремительная сила — это сила, направленная к центру окружности, которая заставляет тело двигаться по круговой траектории, а центробежная сила — это сила, направленная к центру окружности. ощущение, которое испытывает объект, когда он движется по этой круговой траектории, причем это ощущение как бы отталкивает его от центра круга.
Люди испытывают на себе действие центробежной силы, когда поворачивают за угол в машине или когда самолет входит в поворот. Это происходит при отжиме стиральной машины или когда дети катаются на каруселях. Однажды она может даже обеспечить искусственную гравитацию для космических кораблей и космических станций — если мы сможем заставить космический корабль вращаться достаточно быстро, центробежная сила может обеспечить некоторое подобие нормального ощущения гравитации.
Это происходит при отжиме стиральной машины или когда дети катаются на каруселях. Однажды она может даже обеспечить искусственную гравитацию для космических кораблей и космических станций — если мы сможем заставить космический корабль вращаться достаточно быстро, центробежная сила может обеспечить некоторое подобие нормального ощущения гравитации.
Но центробежную силу часто путают с ее аналогом, центростремительной силой, потому что они очень тесно связаны — по сути, это две стороны одной медали.
Центростремительная сила — это название, данное любой силе, которая заставляет объект двигаться по кругу — подумайте о камне, привязанном к концу веревки, а другой конец — к чему-то или в вашей руке. Когда струна закручена, натяжение этой струны не дает камню улететь по прямой линии. Это напряжение направлено внутрь, к центру круга. В качестве другого примера, гравитация Солнца обеспечивает центростремительную силу, которая заставляет планеты двигаться по своим орбитам.
Центростремительная сила всегда направлена перпендикулярно направлению движения объекта. Если вы едете в машине, а дорога изгибается и поворачивает влево, нормальная сила от дороги с креном будет толкать машину влево. Если бы центростремительная сила внезапно исчезла, автомобиль продолжал бы двигаться прямолинейно.
С другой стороны, центробежная сила — это кажущаяся сила, которую ощущает объект, когда он движется по криволинейной траектории, и эта кажущаяся сила направлена в направлении от центра траектории вращения, согласно Кристоферу С. Бэрду. в West Texas A&M University (открывается в новой вкладке).
Центробежная сила направлена наружу, а центростремительная притягивает вращающийся объект внутрь. (Изображение предоставлено: Future)
Обратите внимание, что хотя центростремительная сила является фактической силой, центробежная сила определяется как кажущаяся сила. Другими словами, при вращении массы на струне струна воздействует на массу внутренней центростремительной силой, в то время как масса «кажется» воздействующей на струну внешней центробежной силой.
«Разница между центростремительной и центробежной силой связана с разными «системами отсчета», то есть с разными точками зрения, с которых вы что-то измеряете», — сказал Эндрю А. Ганс, физик-исследователь из Вашингтонского университета. «Центростремительная сила и центробежная сила на самом деле являются одной и той же силой, только в противоположных направлениях, потому что они воспринимаются из разных систем отсчета».
Если вы наблюдаете за вращающейся системой снаружи, вы видите внутреннюю центростремительную силу, которая заставляет вращающееся тело двигаться по окружности. Однако, если вы являетесь частью вращающейся системы, вы испытываете кажущуюся центробежную силу, отталкивающую вас от центра круга, хотя на самом деле вы ощущаете внутреннюю центростремительную силу, которая не дает вам буквально уйти по касательной. .
Вернемся к примеру с автомобилем после поворота с креном. Если вы наблюдаете снаружи, вы можете наблюдать центростремительную силу, толкающую автомобиль внутрь к центру, заставляя его двигаться по кругу.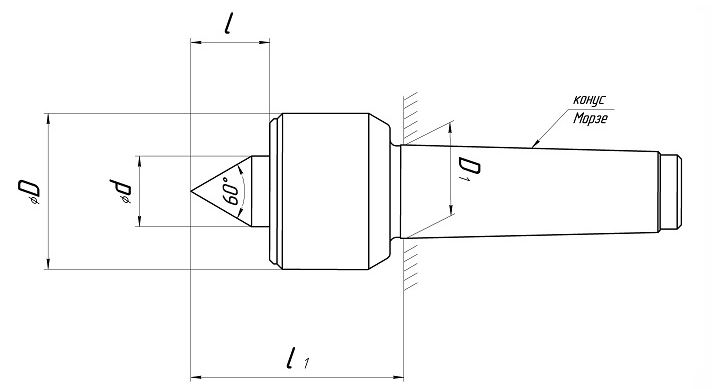 2/r.
2/r.
Третий закон Ньютона гласит, что «на каждое действие есть равное и противоположное противодействие». Точно так же, как гравитация заставляет вас воздействовать на землю, кажется, что земля оказывает равную и противоположную силу на ваши ноги. Когда вы едете в разгоняющемся автомобиле, сиденье оказывает на вас силу, направленную вперед, точно так же, как кажется, что вы оказываете на сиденье силу, направленную назад.
В случае вращающейся системы центростремительная сила притягивает массу внутрь, следуя по кривой траектории, в то время как масса, кажется, выталкивается наружу из-за своей инерции. Однако в каждом из этих случаев прилагается только одна реальная сила, а другая — только кажущаяся сила.
Примеры центростремительной силы
Центростремительная сила используется во многих приложениях. Одним из них является моделирование ускорения космического запуска для подготовки космонавтов. Когда ракета запускается впервые, она настолько загружена топливом и окислителем, что едва может двигаться. Однако по мере подъема он сжигает топливо с огромной скоростью, постоянно теряя массу. Второй закон Ньютона гласит, что сила равна массе, умноженной на ускорение, или F = ma.
Однако по мере подъема он сжигает топливо с огромной скоростью, постоянно теряя массу. Второй закон Ньютона гласит, что сила равна массе, умноженной на ускорение, или F = ma.
В большинстве случаев масса остается постоянной. Однако у ракеты ее масса резко меняется, а сила — в данном случае тяга ракетных двигателей — остается почти постоянной. Это приводит к тому, что ускорение к концу фазы разгона увеличивается в несколько раз по сравнению с нормальной гравитацией. 900:05 НАСА использует большие центрифуги (открывается в новой вкладке), чтобы подготовить астронавтов к этому экстремальному ускорению. В этом случае центростремительная сила создается за счет того, что спинка сиденья давит на космонавта внутрь.
Лабораторные центрифуги быстро вращаются и воздействуют центростремительной силой на жидкости, такие как кровь, которые затем разделяются в зависимости от их плотности. (Изображение предоставлено Shutterstock)
Статьи по теме
Другой пример применения центростремительной силы — лабораторные центрифуги, которые используются для ускорения осаждения взвешенных в жидкости частиц. Одним из распространенных применений этой технологии является подготовка образцов крови для анализа. Согласно Веб-сайт Experimental Biosciences Университета Райса (открывается в новой вкладке): «Уникальная структура крови позволяет очень легко отделить эритроциты от плазмы и других форменных элементов с помощью дифференциального центрифугирования».
Одним из распространенных применений этой технологии является подготовка образцов крови для анализа. Согласно Веб-сайт Experimental Biosciences Университета Райса (открывается в новой вкладке): «Уникальная структура крови позволяет очень легко отделить эритроциты от плазмы и других форменных элементов с помощью дифференциального центрифугирования».
При нормальной силе тяжести тепловое движение вызывает непрерывное перемешивание, что предотвращает осаждение клеток крови из образца цельной крови. Однако типичная лабораторная центрифуга может достигать ускорений, в 600–2000 раз превышающих ускорение в раз при нормальной силе тяжести 9.0006 . Это заставляет тяжелые эритроциты оседать на дно и расслаивает различные компоненты раствора на слои в соответствии с их плотностью.
Эта статья была обновлена 11 ноября 2021 г. редактором Live Science Беном Биггсом.
Дополнительные ресурсы
Подробнее об основах центростремительной силы можно прочитать в Технологического университета Суинберна (открывается в новой вкладке). SciShow предоставляет отличное видео-введение в тему, где они объясните и сравните центростремительную и центробежную силы (откроется в новой вкладке). И Khan Academy предлагает математическое обсуждение темы в этой статье.
SciShow предоставляет отличное видео-введение в тему, где они объясните и сравните центростремительную и центробежную силы (откроется в новой вкладке). И Khan Academy предлагает математическое обсуждение темы в этой статье.
Библиография
Кун, Карл Ф., «Основы физики: руководство для самообучения», Джосси-Басс (2020)
Морин, Дэвид, «Введение в классическую механику», Cambridge University Press (2008)
Бен Биггс — увлеченный и опытный писатель в области науки и техники, автор опубликованных книг и редактор отмеченного наградами журнала How It Works. Он также много лет писал и редактировал материалы для изданий, посвященных технологиям и видеоиграм, позже стал редактором журнала All About Space, а затем журнала Real Crime.
6.1 Угол вращения и угловая скорость – Физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Описывать угол поворота и связывать его с его линейным аналогом
- Опишите угловую скорость и свяжите ее с ее линейным эквивалентом
- Решение задач на угол поворота и угловую скорость
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (4) Научные концепции.
 Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:
Учащийся знает и применяет законы, управляющие движением, в различных ситуациях. Ожидается, что студент:- (C) анализировать и описывать ускоренное движение в двух измерениях с помощью уравнений, включая примеры снарядов и окружностей.
Основные термины раздела
| угол поворота | угловая скорость | длина дуги | круговое движение |
| радиус кривизны | вращательное движение | вращение | тангенциальная скорость |
Угол поворота
Что именно мы подразумеваем под круговым движением или вращением ? Вращательное движение – это круговое движение объекта вокруг оси вращения. Мы обсудим конкретно круговое движение и вращение. Круговое движение — это когда объект движется по круговой траектории. Примеры кругового движения включают гоночный автомобиль, мчащийся по круговой кривой, игрушку, прикрепленную к веревке, которая качается по кругу вокруг вашей головы, или круговое петля-петля на американских горках. Вращение — это вращение вокруг оси, проходящей через центр масс объекта, например, Земля, вращающаяся вокруг своей оси, колесо, вращающееся вокруг своей оси, вращение торнадо на пути разрушения или вращение фигуриста во время выступление на Олимпиаде. Иногда объекты будут вращаться во время кругового движения, например Земля, вращающаяся вокруг своей оси, вращаясь вокруг Солнца, но мы сосредоточимся на этих двух движениях отдельно.
Мы обсудим конкретно круговое движение и вращение. Круговое движение — это когда объект движется по круговой траектории. Примеры кругового движения включают гоночный автомобиль, мчащийся по круговой кривой, игрушку, прикрепленную к веревке, которая качается по кругу вокруг вашей головы, или круговое петля-петля на американских горках. Вращение — это вращение вокруг оси, проходящей через центр масс объекта, например, Земля, вращающаяся вокруг своей оси, колесо, вращающееся вокруг своей оси, вращение торнадо на пути разрушения или вращение фигуриста во время выступление на Олимпиаде. Иногда объекты будут вращаться во время кругового движения, например Земля, вращающаяся вокруг своей оси, вращаясь вокруг Солнца, но мы сосредоточимся на этих двух движениях отдельно.
Поддержка учителей
Поддержка учителей
[BL][OL] Объясните разницу между круговым и вращательным движением, используя вращение Земли вокруг своей оси и ее вращение вокруг Солнца. Объясните, что вращение Земли слегка эллиптическое, хотя и очень близкое к круговому.
Объясните, что вращение Земли слегка эллиптическое, хотя и очень близкое к круговому.
[OL][AL] Попросите учащихся привести примеры кругового движения.
При решении задач, связанных с вращательным движением, мы используем переменные, которые аналогичны линейным переменным (расстояние, скорость, ускорение и сила), но учитывают кривизну или вращение движения. Здесь мы определяем угол поворота, который является угловым эквивалентом расстояния; и угловая скорость, которая является угловой эквивалентностью линейной скорости.
Когда объекты вращаются вокруг какой-либо оси — например, когда диск на рис. 6.2 вращается вокруг своего центра — каждая точка объекта движется по круговой траектории.
Рисунок
6.2
Все точки на компакт-диске движутся по круговым траекториям. Ямки (точки) вдоль линии от центра к краю перемещаются на один и тот же угол ΔθΔθ за время ΔtΔt.
Длина дуги , , это расстояние, пройденное по круговой траектории.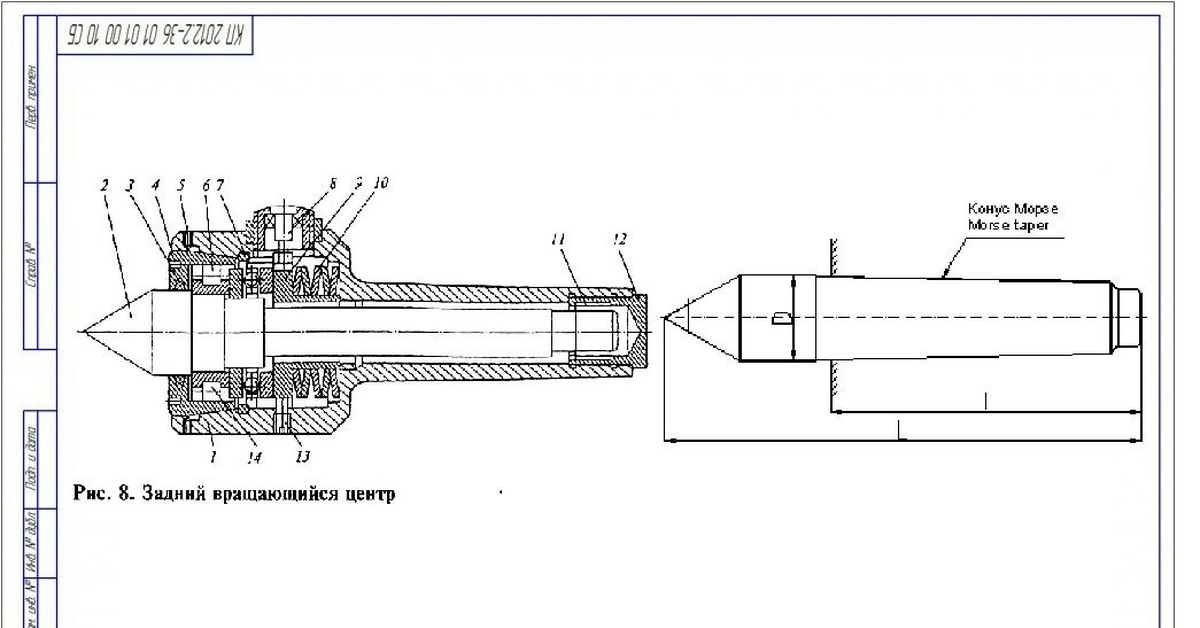 Радиус кривизны, r , является радиусом кругового пути. Оба показаны на рис. 6.3.
Радиус кривизны, r , является радиусом кругового пути. Оба показаны на рис. 6.3.
Рисунок
6.3
Радиус ( r ) окружности повернут на угол ΔθΔθ. Длина дуги, ΔsΔs, представляет собой расстояние, пройденное по окружности.
Рассмотрим линию от центра компакт-диска к его краю. В заданное время каждая яма (используемая для записи информации) на этой линии перемещается на один и тот же угол. Угол поворота представляет собой величину поворота и является угловым аналогом расстояния. Угол поворота ΔθΔθ — это длина дуги, деленная на радиус кривизны.
Δθ=ΔсрΔθ=Δср
Угол поворота часто измеряется в радианах. (Радианы на самом деле безразмерны, потому что радиан определяется как отношение двух расстояний, радиуса и длины дуги.) Оборот — это один полный оборот, когда каждая точка на окружности возвращается в исходное положение. Один оборот покрывает 2π2π радиан (или 360 градусов) и, следовательно, имеет угол поворота 2π2π радиан и длину дуги, равную длине окружности.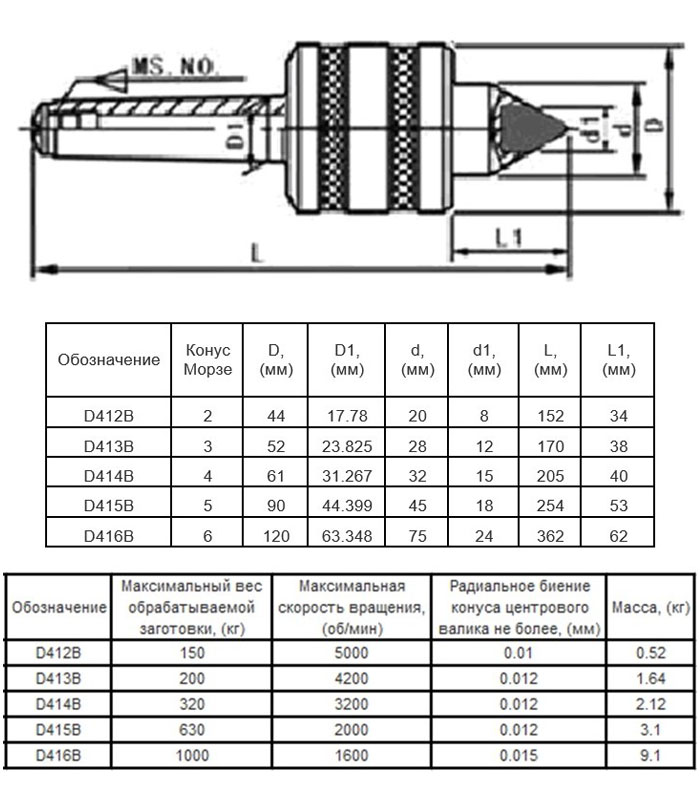 Мы можем преобразовать радианы, обороты и градусы, используя соотношение
Мы можем преобразовать радианы, обороты и градусы, используя соотношение
1 оборот = 2π2π рад = 360°. См. Таблицу 6.1 для преобразования градусов в радианы для некоторых распространенных углов.
2π рад=360°1рад=360°2π≈57,3°2π рад=360°1рад=360°2π≈57,3°
6,1
| Градусы | Радианные меры |
|---|---|
| 30∘30∘ | π6π6 |
| 60∘60∘ | π3π3 |
| 90∘90∘ | π2π2 |
| 120∘120∘ | 2π32π3 |
| 135∘135∘ | 3π43π4 |
| 180∘180∘ | ππ |
Стол
6.1
Обычно используемые углы в градусах и радианах
Угловая скорость
Поддержка учителей
Поддержка учителей
[BL] Просмотр перемещения, скорости, скорости, ускорения.
[AL] Спросите учащихся, изменяется ли скорость при равномерном круговом движении. А как насчет скорости? А ускорение?
Как быстро вращается объект? Мы можем ответить на этот вопрос, используя понятие угловой скорости. Сначала рассмотрим угловую скорость (ω)(ω) — скорость изменения угла поворота. В форме уравнения угловая скорость равна
ω=ΔθΔt,ω=ΔθΔt,
6,2
, что означает, что угловой поворот (Δθ)(Δθ) происходит за время ΔtΔt. Если объект поворачивается на больший угол поворота за заданное время, он имеет большую угловую скорость. Единицами угловой скорости являются радианы в секунду (рад/с).
Теперь рассмотрим направление угловой скорости, а значит, теперь мы должны называть ее угловой скоростью. Направление угловой скорости вдоль оси вращения. Для объекта, вращающегося по часовой стрелке, угловая скорость направлена от вас вдоль оси вращения. Для объекта, вращающегося против часовой стрелки, угловая скорость указывает на вас вдоль оси вращения.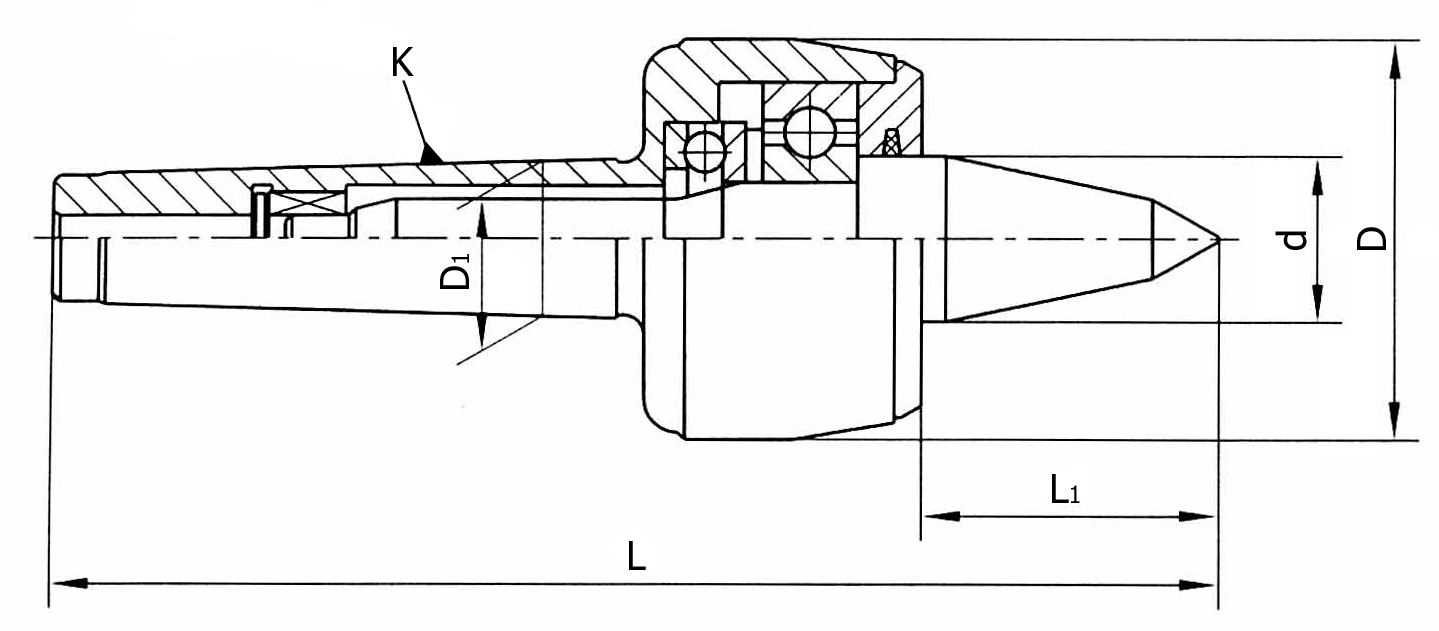
Угловая скорость (ω) является угловой версией линейной скорости v . Тангенциальная скорость – это мгновенная линейная скорость объекта, находящегося во вращательном движении . Чтобы получить точное соотношение между угловой скоростью и тангенциальной скоростью, снова рассмотрим ямку на вращающемся компакт-диске. Эта яма движется по дуге длиной (Δs)(Δs) за короткое время (Δt)(Δt), поэтому ее тангенциальная скорость равна
v=ΔsΔt.v=ΔsΔt.
6.3
Из определения угла поворота Δθ=ΔsrΔθ=Δsr мы видим, что Δs=rΔθΔs=rΔθ . Подставляя это в выражение для v , получаем
v=rΔθΔt=rω.v=rΔθΔt=rω.
Уравнение v=rωv=rω говорит, что тангенциальная скорость v пропорциональна расстоянию r от центра вращения. Следовательно, тангенциальная скорость больше для точки на внешнем краю компакт-диска (с большими r ), чем для точки ближе к центру компакт-диска (с меньшими r ). Это имеет смысл, потому что точка, расположенная дальше от центра, должна пройти большую длину дуги за то же время, что и точка, расположенная ближе к центру. Обратите внимание, что обе точки по-прежнему будут иметь одинаковую угловую скорость, независимо от их расстояния от центра вращения. См. рисунок 6.4.
Это имеет смысл, потому что точка, расположенная дальше от центра, должна пройти большую длину дуги за то же время, что и точка, расположенная ближе к центру. Обратите внимание, что обе точки по-прежнему будут иметь одинаковую угловую скорость, независимо от их расстояния от центра вращения. См. рисунок 6.4.
Рисунок
6.4
Точки 1 и 2 поворачиваются на один и тот же угол (ΔθΔθ), но точка 2 перемещается на большую длину дуги (Δs2Δs2), поскольку она находится дальше от центра вращения.
Поддержка учителей
Поддержка учителей
[AL] Объясните, что период времени ΔtΔt в уравнении, определяющем тангенциальную скорость ( v=ΔsΔtv=ΔsΔt ), должен быть коротким, чтобы дугу, описываемую движущимся объектом, можно было аппроксимировать прямой линией. Это позволяет нам определить направление тангенциальной скорости как касательное к окружности. Это приближение становится все более точным по мере того, как ΔtΔt становится все меньше.
Теперь рассмотрим другой пример: шина движущегося автомобиля (см. рис. 6.5). Чем быстрее вращается шина, тем быстрее движется автомобиль — большое ωω означает большое v , потому что v=rωv=rω. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью ωω, будет производить большую линейную (тангенциальную) скорость, v, для автомобиля. Это связано с тем, что больший радиус означает, что более длинная дуга должна касаться дороги, поэтому автомобиль должен двигаться дальше за то же время.
Рисунок
6,5
Автомобиль, движущийся со скоростью v, вправо, имеет шину, вращающуюся с угловой скоростью ωω. Скорость протектора шины относительно оси составляет v , такая же, как если бы автомобиль был поднят на домкрат и колеса крутились, не касаясь дороги. Непосредственно под осью, где шина касается дороги, протектор шины движется назад относительно оси с тангенциальной скоростью v=rωv=rω, где r — радиус шины.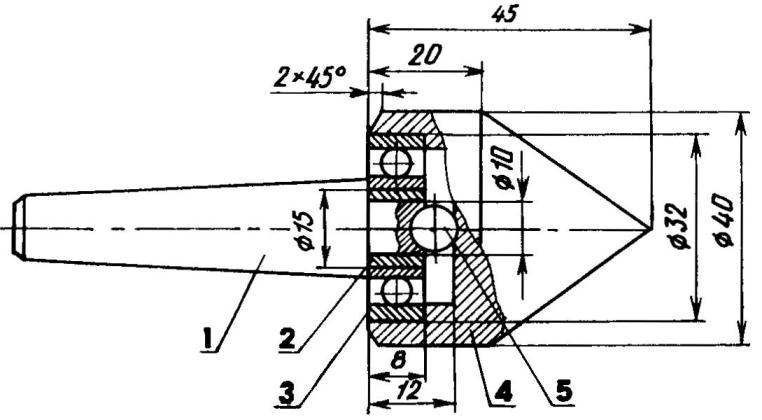 Поскольку дорога неподвижна относительно этой точки шины, автомобиль должен двигаться вперед с линейной скоростью против . Большая угловая скорость шины означает большую линейную скорость автомобиля.
Поскольку дорога неподвижна относительно этой точки шины, автомобиль должен двигаться вперед с линейной скоростью против . Большая угловая скорость шины означает большую линейную скорость автомобиля.
Однако бывают случаи, когда линейная скорость и тангенциальная скорость не эквивалентны, например, когда колеса автомобиля крутятся на льду. В этом случае линейная скорость будет меньше тангенциальной скорости. Из-за отсутствия трения под шинами автомобиля по льду длина дуги, по которой перемещаются протекторы шин, больше, чем линейное расстояние, по которому движется автомобиль. Это похоже на бег на беговой дорожке или вращение педалей на велотренажере; вы буквально никуда не денетесь.
Советы для успеха
Угловая скорость ω и тангенциальная скорость v являются векторами, поэтому мы должны указать величину и направление. Направление угловой скорости находится вдоль оси вращения и указывает от вас для объекта, вращающегося по часовой стрелке, и к вам для объекта, вращающегося против часовой стрелки. В математике это описывается правилом правой руки. Тангенциальная скорость обычно описывается как восходящая, нисходящая, левая, правая, северная, южная, восточная или западная, как показано на рис. 6.6.
В математике это описывается правилом правой руки. Тангенциальная скорость обычно описывается как восходящая, нисходящая, левая, правая, северная, южная, восточная или западная, как показано на рис. 6.6.
Рисунок
6,6
Поскольку муха на краю старой виниловой пластинки движется по кругу, ее мгновенная скорость всегда направлена по касательной к кругу. В этом случае направление угловой скорости находится на странице.
Смотреть физику
Связь между угловой скоростью и скоростью
В этом видео рассматриваются определение и единицы измерения угловой скорости, а также их связь с линейной скоростью. Он также показывает, как конвертировать между оборотами и радианами.
Для объекта, движущегося по круговому пути с постоянной угловой скоростью, изменится ли линейная скорость объекта, если радиус пути увеличится?
Да, потому что тангенциальная скорость не зависит от радиуса.
Да, потому что тангенциальная скорость зависит от радиуса.
Нет, так как тангенциальная скорость не зависит от радиуса.
Нет, так как тангенциальная скорость зависит от радиуса.
Решение задач на угол поворота и угловую скорость
Снап Лаборатория
Измерение угловой скорости
В этом упражнении вы создадите и измерите равномерное круговое движение, а затем сопоставите его с круговыми движениями с разными радиусами.
- Одна струна (длина 1 м)
- Один предмет (резиновая пробка с двумя отверстиями) для привязки к концу
- Один таймер
Процедура
- Привяжите объект к концу строки.
- Раскачивайте объект по горизонтальному кругу над головой (раскачивание запястьем). Важно, чтобы круг был горизонтальным!
- Поддерживайте постоянную скорость объекта при его раскачивании.
- Таким образом измерьте угловую скорость объекта. Измерьте время в секундах, за которое объект совершает 10 оборотов. Разделите это время на 10, чтобы получить угловую скорость в оборотах в секунду, которую вы можете преобразовать в радианы в секунду.
- Какова приблизительная линейная скорость объекта?
- Поднимите руку вверх по веревке так, чтобы длина веревки составила 90 см. Повторите шаги 2–5.
- Переместите руку вверх по веревке так, чтобы ее длина составила 80 см. Повторите шаги 2–5.
- Переместите руку вверх по веревке так, чтобы ее длина составила 70 см.
 Повторите шаги 2–5.
Повторите шаги 2–5. - Переместите руку вверх по веревке так, чтобы ее длина составила 60 см. Повторите шаги 2–5
- Переместите руку вверх по веревке так, чтобы ее длина составила 50 см. Повторите шаги 2–5
- Постройте графики зависимости угловой скорости от радиуса (т.е. длины струны) и линейной скорости от радиуса. Опишите, как выглядит каждый график.
Если медленно раскачивать объект, он может вращаться со скоростью менее одного оборота в секунду. Каковы были бы обороты в секунду для объекта, который делает один оборот за пять секунд? Какова будет его угловая скорость в радианах в секунду?
Объект будет вращаться со скоростью \frac{1}{5}\,\text{об/с}. Угловая скорость объекта будет \frac{2\pi}{5}\,\text{rad/s}.
Объект будет вращаться со скоростью \frac{1}{5}\,\text{об/с}.
 Угловая скорость объекта будет \frac{\pi}{5}\,\text{рад/с}.
Угловая скорость объекта будет \frac{\pi}{5}\,\text{рад/с}.Объект будет вращаться со скоростью 5\,\text{об/с}. Угловая скорость объекта будет 10\pi\,\text{rad/s}.
Объект будет вращаться со скоростью 5\,\text{об/с}. Угловая скорость объекта будет 5\pi\,\text{rad/s}.
Теперь, когда у нас есть понимание концепций угла поворота и угловой скорости, мы применим их к реальным ситуациям башни с часами и вращающейся шины.
Рабочий пример
Угол поворота часовой башни
Часы на башне с часами имеют радиус 1,0 м. а) На какой угол поворачивается часовая стрелка часов, когда она движется с 12 часов дня до 12 часов дня. до 15:00? (b) Какова длина дуги по внешнему краю часов между часовой стрелкой в эти два времени?
до 15:00? (b) Какова длина дуги по внешнему краю часов между часовой стрелкой в эти два времени?
Стратегия
Мы можем вычислить угол поворота, умножив полный оборот (2π2π радиан) на долю 12 часов, покрываемых часовой стрелкой при переходе от 12 к 3. Получив угол поворота, мы можем найти длину дуги, переформулировав уравнение Δθ=ΔsrΔθ=Δsr, поскольку радиус задан.
Решение задачи (a)
При переходе от 12 к 3 часовая стрелка покрывает 1/4 из 12 часов, необходимых для совершения полного оборота. Следовательно, угол между часовой стрелкой в положении 12 и 3 равен 14×2πrad=π214×2πrad=π2 (т. е. 90 градусов).
Решение (б)
Преобразуя уравнение
Δθ=Δsr,Δθ=Δsr,
6,4
получаем
Δs=rΔθ.Δs=rΔ.
6,5
Подстановка известных значений дает длину дуги
Δs=(1,0 м)(π2рад)=1,6 мΔs=(1,0 м)(π2рад)=1,6 м
6,6
Обсуждение3
4 отбрасывать радианы из окончательного решения в часть (b), потому что на самом деле радианы безразмерны.
 Это связано с тем, что радиан определяется как отношение двух расстояний (радиуса и длины дуги). Таким образом, формула дает ответ в метрах, как и ожидалось для длины дуги.
Это связано с тем, что радиан определяется как отношение двух расстояний (радиуса и длины дуги). Таким образом, формула дает ответ в метрах, как и ожидалось для длины дуги.
Рабочий пример
Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость автомобильной шины радиусом 0,300 м, когда автомобиль движется со скоростью 15,0 м/с (около 54 км/ч). См. рисунок 6.5.
Стратегия
В этом случае скорость протектора шины относительно оси шины равна скорости автомобиля относительно дороги, поэтому мы имеем v = 15,0 м/с. Радиус шины равен r = 0,300 м. Так как мы знаем v и r , мы можем изменить уравнение v=rωv=rω, чтобы получить ω=vrω=vr и найти угловую скорость.
Решение
Чтобы найти угловую скорость, мы используем соотношение: ω=vrω=vr .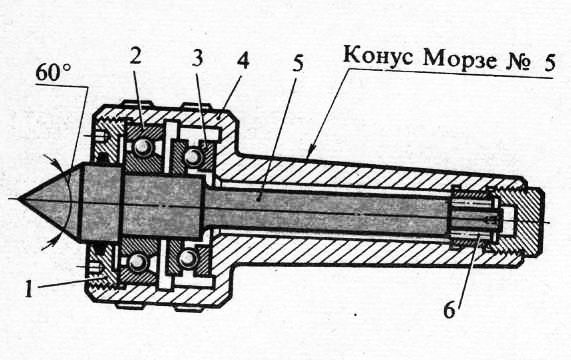
Подстановка известных величин дает
ω=15,0 м/с0,300 м=50,0 рад/с.ω=15,0 м/с0,300 м=50,0 рад/с.
6,7
Обсуждение
Когда мы отбрасываем единицы измерения в приведенном выше расчете, мы получаем 50,0/с (т. е. 50,0 в секунду, что обычно записывается как 50,0 с −1 ). Но угловая скорость должна иметь единицы рад/с. Поскольку радианы безразмерны, мы можем подставить их в ответ для угловой скорости, потому что мы знаем, что движение является круговым. Также обратите внимание, что если бы землеройная машина с колесами гораздо большего размера, скажем, радиусом 1,20 м, двигалась с той же скоростью 15,0 м/с, его колеса вращались бы медленнее. Они будут иметь угловую скорость
ω=15,0 м/с1,20м=12,5рад/сω=15,0м/с1,20м=12,5рад/с
6,8
Практические задачи
1.
Чему равен угол в градусах между часовой и минутной стрелками часов, показывающих 9 часов утра?
- 0°
- 90°
- 180°
- 360°
2.
Какова приблизительная длина дуги между часовой и минутной стрелками часов, показывающих 10:00, если радиус часов равен 0,2 м?
- 0,1 м
- 0,2 м
- 0,3 м
- 0,6 м
Проверьте свое понимание
3.
Что такое круговое движение?
Круговое движение — это движение объекта по линейной траектории.
Круговое движение — это движение объекта по зигзагообразной траектории.
Круговое движение — это движение объекта по круговой траектории.

Вариант D сбивает с толку как дистрактор
4.
Что понимается под радиусом кривизны при описании вращательного движения?
- Радиус кривизны — это радиус кругового пути.
- Радиус кривизны — это диаметр кругового пути.
- Радиус кривизны — это длина окружности кругового пути.
- Радиус кривизны — это площадь кругового пути.
5.
Что такое угловая скорость?
Угловая скорость – это скорость изменения диаметра кругового пути.
Угловая скорость – это скорость изменения угла, образуемого круговой траекторией.

Угловая скорость – это скорость изменения площади кругового пути.
Угловая скорость — это скорость изменения радиуса кругового пути.
6.
Какое уравнение определяет угловую скорость ω, если r — радиус кривизны, θ — угол, t — время?
\omega = \frac{\Delta\theta}{\Delta{t}}
\omega = \frac{\Delta{t}}{\Delta\theta}
\omega = \frac{\Delta{r}}{\Delta{t}}
\omega = \frac{\Delta{t}}{\Delta{r}}
7.
Найдите три примера объекта, движущегося по кругу.
искусственный спутник Земли, гоночный автомобиль, движущийся по кольцевой гоночной трассе, и волчок, вращающийся вокруг своей оси
искусственный спутник на орбите Земли, гоночный автомобиль, движущийся по круговой гоночной трассе, и мяч, привязанный к веревке, раскачивается по кругу вокруг головы человека
Земля вращается вокруг своей оси, гоночный автомобиль движется по кольцевой гоночной трассе, а мяч, привязанный к веревке, раскручивается по кругу вокруг головы человека
Земля, вращающаяся вокруг своей оси, лопасти работающего потолочного вентилятора и волчок, вращающийся вокруг своей оси
8.
Какова относительная ориентация векторов радиуса и тангенциальной скорости объекта при равномерном круговом движении?
Вектор тангенциальной скорости всегда параллелен радиусу окружности, по которой движется объект.
Вектор тангенциальной скорости всегда перпендикулярен радиусу окружности, по которой движется объект.
Вектор тангенциальной скорости всегда находится под острым углом к радиусу окружности, по которой движется объект.
Вектор тангенциальной скорости всегда находится под тупым углом к радиусу окружности, по которой движется объект.

 Тип LC-NC
Тип LC-NC
Всего комментариев: 0