По признаку характера зависимости от времени модели делят на: Классификация моделей

Классификация математических моделей — Информатика, информационные технологии

В качестве основного классификационного признака для ММ целесообразно использовать свойства операторов моделирования исхода операции и оценивания показателя ее эффективности [12, 35].

Оператор моделирования исхода Н может быть функциональным (т. е. заданным системой аналитических функций) или алгоритмическим (т. е. содержать математические, логические и логико-лингвистические операции, не приводимые к последовательности аналитических функций). Кроме того, он может быть детерминированным (когда каждому элементу множества U ´ ? соответствует детерминированное подмножество значений выходных характеристик модели Y или стохастическим (когда каждому значению множества U ´ ? соответствует случайное подмножество ).

Оператор, оценивания показатель эффективности ?, может задавать либо точечно-точечное преобразование (когда каждой точке множества выходных характеристик Y ставится в соответствие единственное значение показателя эффективности W), либо множественно-точечное преобразование (когда показатель эффективности задается на всем множестве полученных в результате моделирования значений выходных характеристик модели).

В зависимости от свойств названных операторов все ММ делятся на три основных класса: аналитические, статистические, имитационные.

Для аналитических моделей характерна детерминированная функциональная связь между элементами множеств U, ?, Y, а значение показателя эффективности W определяется с помощью точечно-точечного отображения. Аналитические модели имеют весьма широкое распространение. Они хорошо описывают качественный характер (основные тенденции) поведения исследуемых систем. В силу простоты их реализации на ЭВМ и высокой оперативности получения результатов такие модели часто применяются при решении задач синтеза систем, а также при оптимизации вариантов применения в различных операциях.

К статистическим относят ММ систем, у которых связь между элементами множеств U, ?, Y задается функциональным оператором Н, а оператор ?является множественно-точечным отображением, содержащим алгоритмы статистической обработки. Такие модели применяются в тех случаях, когда результат операции является случайным, а конечные функциональные зависимости, связывающие статистические характеристики учитываемых в модели случайных факторов с характеристиками исхода операции, отсутствуют. Причинами случайности исхода операции могут быть случайные внешние воздействия; случайные характеристики внутренних процессов; случайный характер реализации стратегий управления. В статистических моделях сначала формируется представительная выборка значений выходных характеристик модели, а затем производится ее статистическая обработка с целью получения значения скалярного или векторного показателя эффективности.

Имитационными называются ММ систем, у которых оператор моделирования исхода операции задается алгоритмически. Когда этот оператор является стохастическим, а оператор оценивания показателя эффективности задается множественно-точечным отображением, имеем классическую имитационную модель, которую более подробно рассмотрим в гл. 9. Если оператор H является детерминированным, а оператор ? задает точечно-точечное отображение, можно говорить об определенным образом вырожденной имитационной модели.

На рис. 8.2 представлена классификация наиболее часто встречающихся математических моделей по рассмотренному признаку.

Важно отметить, что при создании аналитических и статистических моделей широко используются их гомоморфные свойства (способность одних и тех же ММ описывать различные по физической природе процессы и явления). Для имитационных моделей в наибольшей степени характерен изоморфизм процессов и структур, т. е. взаимно однозначное соответствие элементов структур и процессов реальной системы элементам ее математического описания и соответственно модели.

Согласно [53], изоморфизм — соответствие (отношение) между объектами, выражающее тождество их структуры (строения). Именно таким образом организовано большее число классических имитационных моделей. Названное свойство имитационных моделей проиллюстрировано рис. 8.3.

Имитационные модели являются наиболее общими ММ. В силу этого иногда все модели называют имитационными [55]:

• аналитические модели, «имитирующие» только физические законы, на которых основано функционирование реальной системы, можно рассматривать как имитационные модели I уровня;
• статистические модели, в которых, кроме того, «имитируются» случайные факторы, можно называть имитационными моделями II уровня;
• собственно имитационные модели, в которых еще имитируется и функционирование системы во времени, называют имитационными моделями III уровня.

Классификацию ММ можно провести и по другим признакам [53].

На рис. 8.4 представлена классификация моделей (прежде всего аналитических и статистических) по зависимости переменных и параметров от времени. Динамические модели, в которых учитывается изменение времени, делятся на стационарные (в которых от времени зависят только входные и выходные характеристики) и нестационарные (в которых от времени могут зависеть либо параметры модели, либо ее структура, либо и то, и другое). На рис. 8.5 показана классификация ММ еще по трем основаниям: по характеру изменения переменных; особенностям используемого математического аппарата; способу учета проявления случайностей. Названия типов (видов) моделей в каждом классе достаточно понятны. Укажем лишь, что в сигнально-стохастических моделях случайными являются только внешние воздействия на систему. Имитационные модели, как правило, можно отнести к типам:

• по характеру изменения переменных — к дискретно-непрерывным моделям;
• математическому аппарату — к моделям смешанного типа;
• способу учета случайности — к стохастическим моделям общего вида.

Статьи к прочтению:

• Классификация материнских плат по форм-фактору
• Классификация методов доступа

Математическое моделирование. Выбор модели. Грунтовое основание. Модель Винклера и Пастернака.

Похожие статьи:

• Классификация и формы представления моделей

  При классификации по области использования модели бывают … — информационные — материальные — статические — научно-технические По области использования…

• Классификация моделей надежности по

  Термин модель надежности программного обеспечения, как правило, относится к математической модели, построенной для оценки зависимости надежности…

2. Классификация моделей.

Поскольку
общим свойством любых моделей является
способность отражать существенные для
целей исследования характеристики
исследуемых объектов, то наиболее
существенными признаками моделей
следует считать:

степень
абстрагирования от оригинала;

характер
моделируемой стороны объекта;

степень
формализации предметной области.

Классификация
моделей по этим признакам представлена
на рис. 1.

По
степени абстрагирования модели от
оригинала
модели подразделяются на материальные
(физические), теоретические, комбинированные.

К
классу физических моделей относятся:

пространственно
подобные модели, отличительным признаком
которых является геометрическое подобие
между объектом и моделью;

модели,
у которых процесс функционирования
такой же как у оригинала.

Можно
выделить следующие виды физических
моделей: натурные, масштабные и аналоговые.

Натурные
модели — это, как правило, прообразы
реальных исследуемых систем. Их обычно
называют стендами, макетами и опытными
образцами. Натурные модели имеют почти
полную адекватность с системой-оригиналом,
что обеспечивает высокую точность и
достоверность результатов моделирования.
Во время стендовых и комплексных
испытаний выявляются общие закономерности
системы, накапливаются опытные данные,
обработка которых позволяет получить
обобщенные сведения о значениях
характеристик существенных свойств
исследуемых процессов и систем.

Яркий
исторический пример натурной модели —
построенная по приказу Суворова А.В.
крепостная стена для отработки штурма
Измаила. Однако натурное моделирование
для систем военного назначения не всегда
осуществимо.

Масштабная
модель — это система той же физической
природы, что и оригинал, но отличающаяся
от него масштабами. Методологической
основой масштабного моделирования
является теория подобия, которая
предусматривает соблюдение геометрического
подобия оригинала и модели и соответствующих
масштабов их существенных параметров.

а)
по

степень
абстрагирования модели от оригинала

Материальные
Теоретические Комбинированные

(физические)

натурные
математические

масштабные
словесно-описательные

аналоговые
графические

б)
по
характеру моделируемой стороны объекта

Моделирование
Моделирование

структуры
поведения (функционирования)

объекта
объекта

в)
по
степени формализации предметной области

Вербальные
Концептуальные Формальные

Рис.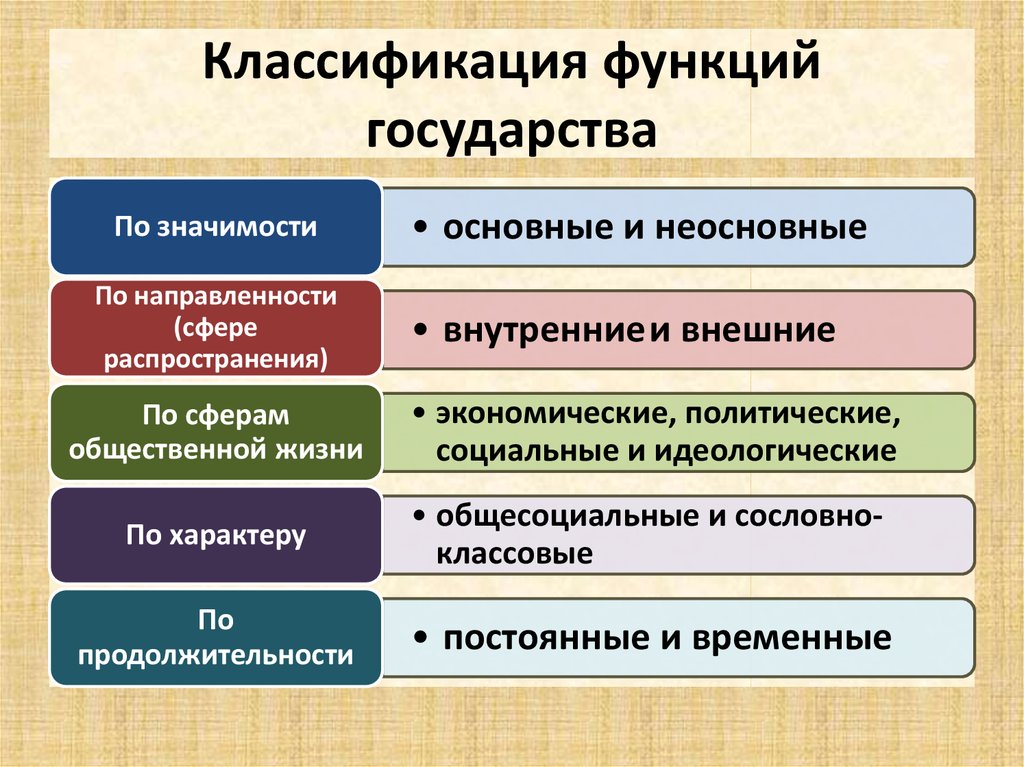
1. Классификация моделей

Аналоговыми
моделями называются системы, имеющие
физическую природу, отличающуюся от
оригинала, но сходные с оригиналом
процессы функционирования. Обязательным
условием при этом является однозначное
соответствие между параметрами изучаемого
объекта и его модели. Для создания
аналоговой модели, как правило, требуется
наличие математического описания
процессов, протекающих в изучаемой
системы.

Теоретические
модели подразделяются на математические,
словесно-описательные, образные и
графические.

Математическая
модель представляет собой формализованное
описание системы с использованием
различных математических соотношений
— формул, уравнений, матриц и т. п.

К
математическим относят достаточно
широкий класс моделей. Они обеспечивают
поиск и оценку рациональных решений,
не прибегая к натурным испытаниям.

Математические
модели позволяют получать результаты,
обладающие высокой точностью. С ростом
возможностей ЭВМ математические модели
находят все более широкое применение.

Классификация
математических
моделей представлена в таблице 1.

Таблица 1

Классификационный признак	Наименование классов математических моделей
Форма представления модели	Аналитические, алгоритмические (программные) или имитационные
Применяемый математический аппарат	Массового обслуживания, Игровые, Математического программирования Представления знаний
Возможности модели	Оценочные Оптимизационные
Характер процессов в системе	Детерминированные Стохастические
Тип параметров	Дискретные Непрерывные
Учет времени	Статистические Динамические
Число этапов моделирования	Одноэтапные Многоэтапные

По
форме представления математические
модели разделяются на аналитические и
алгоритмические (программные) или
имитационные.

В
аналитических моделях зависимость
между переменными, описывающими модель,
является математическим выражением
или системой таких выражений. Решение
на основе аналитических моделей может
быть получено в результате однократного
просчета безотносительно к конкретным
значениям характеристик. Как правило,
аналитические модели удаётся построить
для сравнительно несложных систем.

Создание
ЭВМ обусловило появление новой формы
математической модели — алгоритмической
(особенности применения термина
“программная модель” приведены ниже).
Алгоритм позволяет описать поведение
или структуру системы и провести с
такой моделью ряд машинных (вычислительных)
экспериментов. Характерной особенностью
такой модели является то, что
последовательность шагов их воспроизведения
(прогона) на ЭВМ (выполнение алгоритма)
соответствует поведению моделируемой
системы, т. е. имитирует поведение системы
во времени. Такую модель часто называют
имитационной, а процесс исследования
— имитационным.

В
случае, когда процесс, протекающий в
моделируемой системе, носит стохастический
характер, для нахождения характеристик
этого процесса требуется многократное
его воспроизведение на ЭВМ с последующей
статистической обработкой результатов.
В качестве метода реализации такого
процесса используется метод статистического
моделирования, являющийся обобщением
понятия имитационного моделирования.

По
применяемому математическому аппарату
при проведении системных исследований
различают модели: массового обслуживания,
сетевые, игровые, математического
программирования, представления знаний
и др.

С
точки зрения предоставляемых возможностей
можно выделить оценочные и оптимизационные
модели.

Оценочные
модели позволяют оценить эффективность
принимаемых решений, а в частном случае
— оценить значения характеристик
существенных свойств системы. Для поиска
рационального (эффективного) решения
требуется многократный прогон модели
для различных вариантов исходных данных.
Примером оценочной модели может служить
модель, описываемая системой массового
обслуживания.

Оптимизационные
модели наряду с оценкой эффективности
позволяют находить непосредственно и
само рациональное решение. К оптимизационным
относятся некоторые аналитические
модели, например, основанные на применении
градиентных методов.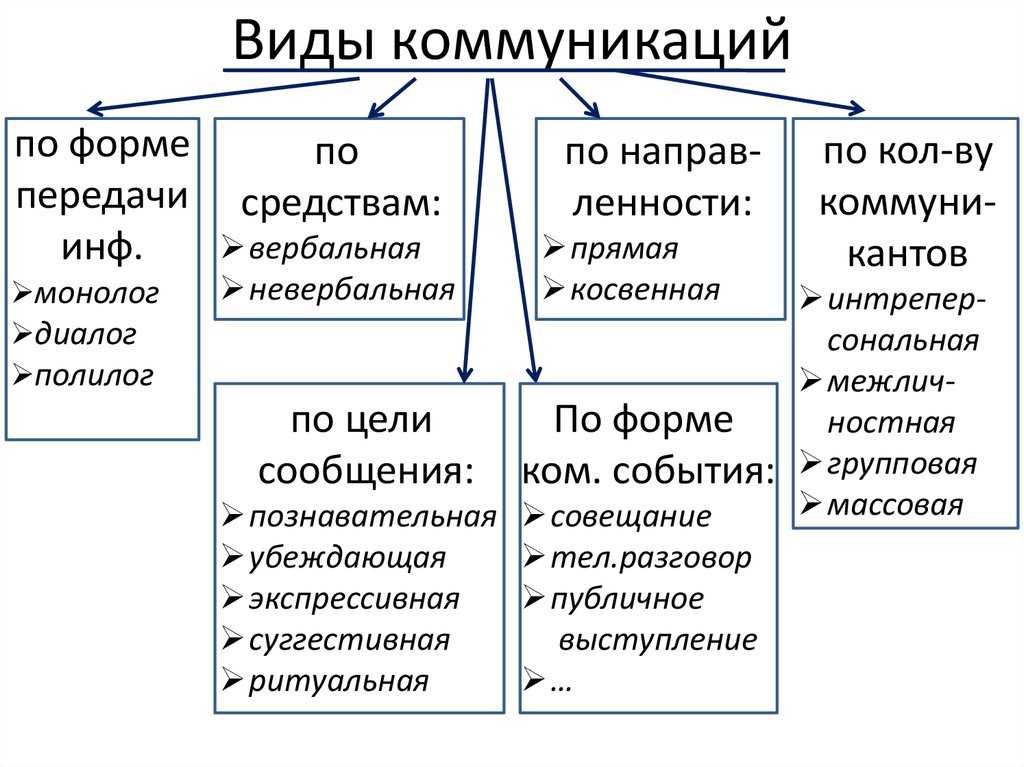

По
характеру процессов, протекающих в
моделируемой системе, выделяют
детерминированные и стохастические
модели.

Детерминированные
модели отображают процессы, в которых
отсутствуют какие-либо случайные
воздействия. Стохастические же модели
учитывают вероятностный характер
процессов (явлений, событий), протекающих
в системе. Обычно с помощью этих моделей
определяются средние значения
характеристик существенных свойств
системы.

Как
известно, параметры систем могут быть
дискретными и непрерывными.
Соответственно различают дискретные
и непрерывные модели.

С
точки зрения учета или не учета времени
различают динамические и статистические
модели. В первом случае ряд параметров
системы являются функциями от времени.
Во втором случае такой зависимости нет.

По
числу этапов модели делят на одноэтапные
и многоэтапные. Каждый этап при этом
ассоциируется с достижением определенной
цели.

Следующим
представителем теоретических моделей
в приведенной классификации выступают
словесно-описательные модели. К ним
относят описания систем и процессов,
представленные в виде текстов на
естественном языке. Характерным для
этих моделей является их универсальность,
широкая доступность и зачастую
неоднозначность. Они находят применение,
как правило, на начальных этапах
исследования системы. Разновидностью
словесно-описательных моделей являются
знаковые модели, в которых для выражения
свойств оригинала используются условные
знаки (символы).

К
образным моделям относятся модели,
сконструированные из наглядных элементов,
отражающих некоторые свойства структуры
и поведения системы. Разновидностью
образного моделирования являются
гипотетическое моделирование и
макетирование. Эти модели используются,
как правило, на начальных этапах
исследования либо при обучении.

В
основе гипотетического моделирования
лежит некоторая гипотеза, высказанная
исследователем о характере исследуемых
процессов в системе и отражающая его
уровень знаний об объекте исследования.
При макетировании на основе изучения
причинно-следственных связей создается
макет, функционирование которого
адекватно отражает явления и процессы,
протекающие в оригинале.

К
графическим моделям следует отнести
различные графики, чертежи, монограммы,
схемы, которые отражают соотношения
параметров в исследуемой системе и
позволяют осуществлять прогнозирование
характера их изменения.

И,
наконец, существуют модели, которые
совмещают в себе признаки как материальных,
так и математических моделей. Такие
модели носят название комбинированных
моделей (полунатурных, квазинатурных,
математико-физических и др.). Этот вид
моделей используется в тех случаях,
когда исследуемый объект невозможно
(нецелесообразно) представить с помощью
моделей одного вида. Та часть объекта,
которая не поддается математическому
описанию, моделируется, например,
физически, остальная — знаково. Таковы
командно-штабные учения (КШУ) на картах,
когда работа штабов проигрывается
физически, а действия сил в море отражаются
лишь в документах.

Вторым
классификационным признаком
в приведенной выше классификации моделей
выступает характер моделируемой стороны
объекта. Исходя из этого признака
различают моделирование структуры и
поведения (функционирования) объекта.

Третьим
основанием классификации
моделей выступает степень формализации
предметной области. Исходя из этого
признака можно выделить три вида моделей:
вербальные, концептуальные, формальные.

Вербальная
модель представляет собой описание
объекта исследования на естественном
языке. Основным требованием к вербальной
модели является полнота описания
предметной области.

В
концептуальной модели конкретизируется
цель функционирования системы (вплоть
до требований), определяются принципы
построения и функционирования, структура,
алгоритмы функционирования, существенные
свойства и их показатели, основные
термины и определения и др. Концептуальная
модель — это субстрат системы с позиций
достижения целей моделирования.
Разработка концептуальной модели
требует достаточно глубоких знаний
о системе, поскольку необходимо
обосновывать не только то, что должно
войти в модель, но и то, что может быть
отброшено без существенных искажений
результатов моделирования. Основная
проблема при создании модели заключается
в нахождении компромисса между степенью
её сложности и адекватностью исследуемой
системе.

Формальная
модель является продолжением (развитием)
концептуальной модели с точки зрения
дальнейшей формализации структуры и
процесса функционирования системы. В
конечном счете именно с ее помощью
реализуется основная цель моделирования
— изучение свойств оригинала.

Как растет популяция: экспоненциальные и логистические уравнения

Самый простой способ уловить идею растущей популяции — использовать одноклеточный организм, такой как бактерия или инфузория. На рисунке 1 изображена популяция из Paramecium в небольшом предметном стекле лабораторной депрессии. В этой популяции особи делятся один раз в сутки. Таким образом, начиная с одной особи в день 0, мы ожидаем, что в последующие дни популяция будет состоять из 2, 4, 8, 16, 32 и 64 особей. Мы можем видеть здесь, что в любой конкретный день количество особей в популяции просто вдвое превышает число, которое было за день до этого, поэтому сегодняшнее число, назовем его 9.0003 N (сегодня), равно удвоенному числу вчера, назовем его N (вчера), что можно записать более компактно как N (сегодня) = 2 N (вчера).

Поскольку основное правило клеточного деления применимо не только к сегодняшнему и вчерашнему дню, но и к любому дню вообще, мы получили бы N (6) = 2 N (5), или N (4) = 2 N (3) и т. д.

Поэтому имеет смысл записать это как N ( t ) = 2 N ( t — 1) где t может принимать любое значение.

Теперь мы можем немного обобщить эту идею, если заметим, что на шестой день число равно удвоенному числу на пятый день, или N (6) = 2 N (5), а на пятый день число равно удвоенному числу на четвертый день, или N (5) = 2 N (4) и т. д. 5) — который, как мы знаем, равен 2 N (4) — получаем N (6) = 2[2 N (4)], что равно N (6) = 22 N (4).

Но N (4) = 2 N (3), поэтому мы можем заменить N (4), получив N (6) = 22 N (4) = 22[2 N (3)] = 23 N (3). И если мы будем следовать той же схеме, мы увидим, что N(3) = 23 N (0), что мы можем заменить на N (3), чтобы получить N (6) = 26 Н (0).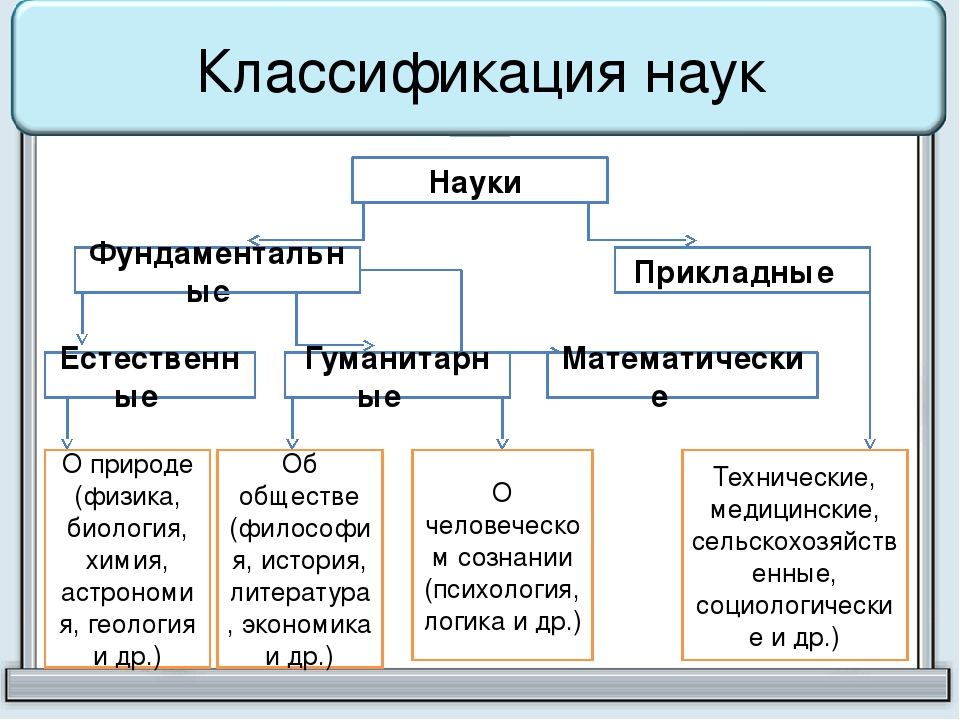 Таким образом, мы можем увидеть относительно простое обобщение, а именно

, где t обозначает любое время вообще (например, если t = 6, N (6) = 26[ N (0)]).

Наконец, отметим, что это уравнение было получено из конкретной ситуации, показанной на рисунке 1, где одно деление в день было жестким правилом. Вот откуда двойка в уравнении 1 — от каждой особи Paramecium мы получаем две особи на следующий день. Конечно, скорость деления может быть любой. Если бы в день происходило два деления, но всегда погибала бы одна клетка, мы бы ожидали, что от каждой отдельной особи будет по три особи, и уравнение 1 будет равно 9.0003 Н (t) = 3 t Н (0). Таким образом, скорость деления может быть вообще любым числом, и общее уравнение принимает вид

, где R обычно называют конечной скоростью прироста популяции (в реальном случае деления Paramecium конечная скорость прироста популяции равна к скорости деления). На рисунке 2 мы иллюстрируем это уравнение для различных значений R . Обычно его называют экспоненциальным уравнением, а форма данных на рисунке 2 является общей формой, называемой экспоненциальной.

Рисунок 2: Слева: общая форма экспоненциального роста населения (уравнение 2). Справа: фактическое количество Paramecium в образце 1 мл лабораторной культуры.

Любое значение R может быть представлено бесконечным числом способов (например, если R = 16, мы могли бы написать R = 8 x 2, или R = 42, или R = 32/). 2, или р = 2,718282,77). В этом последнем выражении ( R = 2,718282,77) используется важная константа, которую можно вспомнить из элементарного исчисления, — постоянная Эйлера. Выражение любого значения R в виде постоянной Эйлера, возведенной в некоторую степень, на самом деле чрезвычайно полезно — оно привносит в картину всю мощь исчисления. Если мы обозначим постоянную Эйлера как e мы можем записать Уравнение 2 как

Теперь, если мы возьмем натуральный логарифм обеих частей Уравнения 3 — вспомните ln ( ex ) = x — Уравнение 3 станет: ln

3 [

4 ( t )] = ln [ N (0)] + rt

И если мы начали популяцию с одной особи (как в приведенном выше примере), мы имеем

, из которых мы видим, что естественный логарифм популяции в любой конкретный момент времени является некоторой постоянной величиной, умноженной на это время. . Постоянная r называется собственной нормой естественного прироста (рис. 2).

Все виды микроорганизмов демонстрируют закономерности, очень близкие к экспоненциальному росту популяции. Например, на правом графике рисунка 2 представлена ​​популяция Paramecium , растущая в лабораторной культуре. Модель роста очень близка к модели экспоненциального уравнения.

Другой способ записи показательного уравнения — дифференциальное уравнение, т. е. представление роста населения в его динамической форме. Вместо того, чтобы спрашивать, какова численность населения в момент времени t , мы спрашиваем, с какой скоростью растет население в момент t . Скорость обозначается как dN / dt , что просто означает «изменение N по отношению к изменению t », и если вы вспомните свои базовые вычисления, мы можем найти скорость роста, дифференцируя уравнение 4, что дает нам

, что довольно примечательно, потому что это говорит о том, что скорость роста логарифмического числа в популяции постоянна. Эта постоянная скорость роста журнала населения является внутренней скоростью роста.

Напомним, что скорость изменения логарифма числа такая же, как и изменение этого числа на душу населения, что означает, что мы можем записать уравнение 5 как

, где мы опускаем переменную t , поскольку она очевидно, куда он идет, а затем мы немного перестраиваем, чтобы получить

, где параметр r снова является внутренней нормой естественного прироста. Основное соотношение между конечной скоростью роста и внутренней скоростью составляет

r = ln ( R )

, где ln относится к натуральному логарифму. Обратите внимание, что Уравнение 6 и Уравнение 3 — это просто разные формы одного и того же уравнения (Уравнение 3 — это интегрированная форма Уравнения 6, Уравнение 6 — дифференцированная форма Уравнения 3), и оба они могут называться просто экспоненциальными уравнениями.

Рисунок 3: Гипотетический случай популяции вредителей в агроэкосистеме

Согласно модели 1 (которая имеет относительно большую оценку R), фермер должен подумать о применении процедуры контроля примерно в середине сезона. Согласно модели 2 (с относительно небольшой оценкой R) фермеру вообще не нужно беспокоиться о борьбе с вредителем, поскольку его популяция превышает экономический порог только после сбора урожая. Понятно, что важно знать, какая модель правильная. В этом случае, согласно имеющимся данным (синие точки данных), либо модель 1, либо модель 2, по-видимому, обеспечивают хорошее соответствие, оставляя фермера в подвешенном состоянии.

Экспоненциальное уравнение является полезной моделью простых популяций, по крайней мере, для относительно коротких периодов времени. Например, если лаборанту необходимо знать, когда бактериальная культура достигает определенной плотности популяции, можно использовать экспоненциальное уравнение, чтобы точно спрогнозировать, когда будет достигнута эта численность популяции. Другой пример касается сельскохозяйственных вредителей. Травоядные всегда являются потенциально серьезной проблемой для растений. Когда растения, подвергающиеся таким вспышкам, являются сельскохозяйственными, то есть сельскохозяйственными культурами, потери могут быть очень значительными как для фермера, так и для потребителя.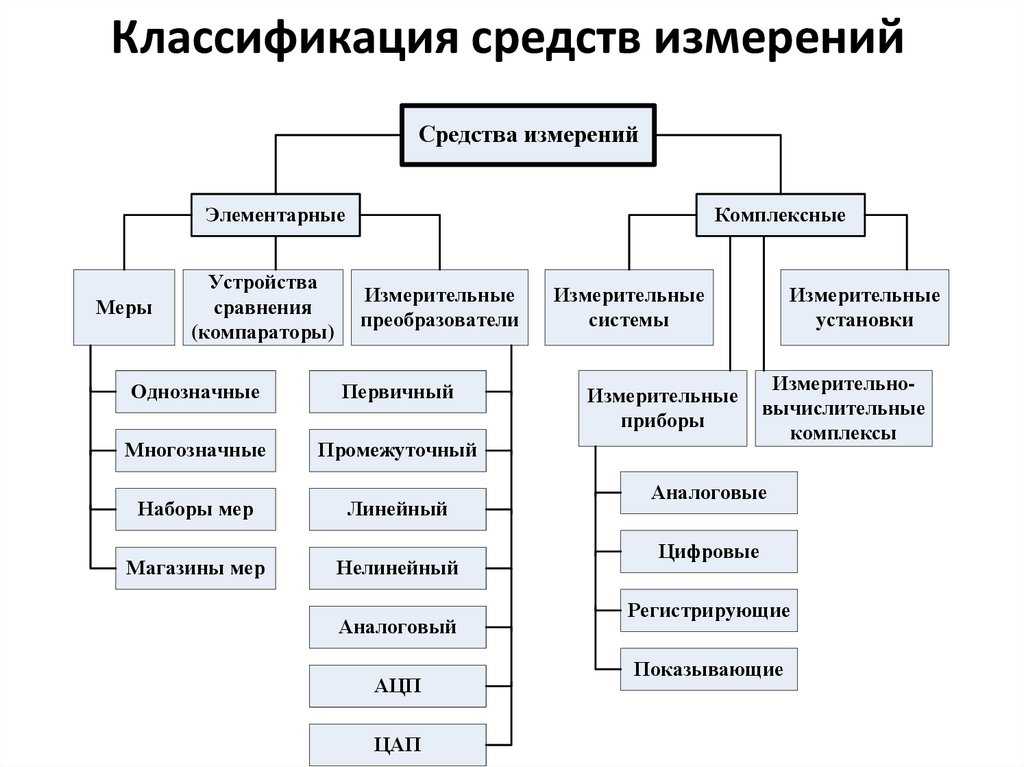 Таким образом, всегда есть необходимость предотвратить такие вспышки. После Второй мировой войны основным оружием в борьбе с такими вспышками вредителей были химические пестициды, такие как ДДТ. Однако в последние годы мы пришли к пониманию того, что эти пестициды чрезвычайно опасны в долгосрочной перспективе как для окружающей среды, так и для людей. Следовательно, было движение за ограничение количества пестицидов, распыляемых для борьбы с вредителями. Основной способ сделать это — установить экономический порог, который представляет собой плотность популяции потенциального вредителя, ниже которой ущерб урожаю незначителен (т. Е. На самом деле нет необходимости в опрыскивании). Когда популяция вредителей превышает этот порог, фермеру необходимо принять меры и применить какой-либо пестицид или другие средства борьбы с вредителями. Учитывая характер этой проблемы, иногда крайне важно иметь возможность предсказать, когда вредитель достигнет экономического порога. Зная R для видов вредителей позволяет фермеру предсказать, когда потребуется применить какую-либо процедуру борьбы (рис. 3).

Показательное уравнение также является полезной моделью для развития интуитивных представлений о популяциях. Классический пример — пруд с кувшинками. Если каждая подушечка кувшинки воспроизводит себя (две подушечки занимают место одной подушечки) каждый месяц, и пруду потребовалось, скажем, три года, чтобы наполовину заполниться подушечками кувшинок, сколько времени потребуется пруду? быть полностью покрытым кувшинками? Если вы не перестанете думать слишком ясно, заманчиво сказать, что потребуется столько же времени, три года, чтобы вторая половина пруда стала такой же наполненной, как и первая. Ответ, конечно, один месяц.

Другим популярным примером является известный древнеегипетский (а иногда и персидский) математик, который просит у царя плату в виде зерен пшеницы (иногда риса). Одна крупинка на первой клетке шахматной доски, две крупинки на второй клетке и так далее до последней клетки. Фараон не может себе представить, что такая простая плата может иметь большое значение, и поэтому соглашается.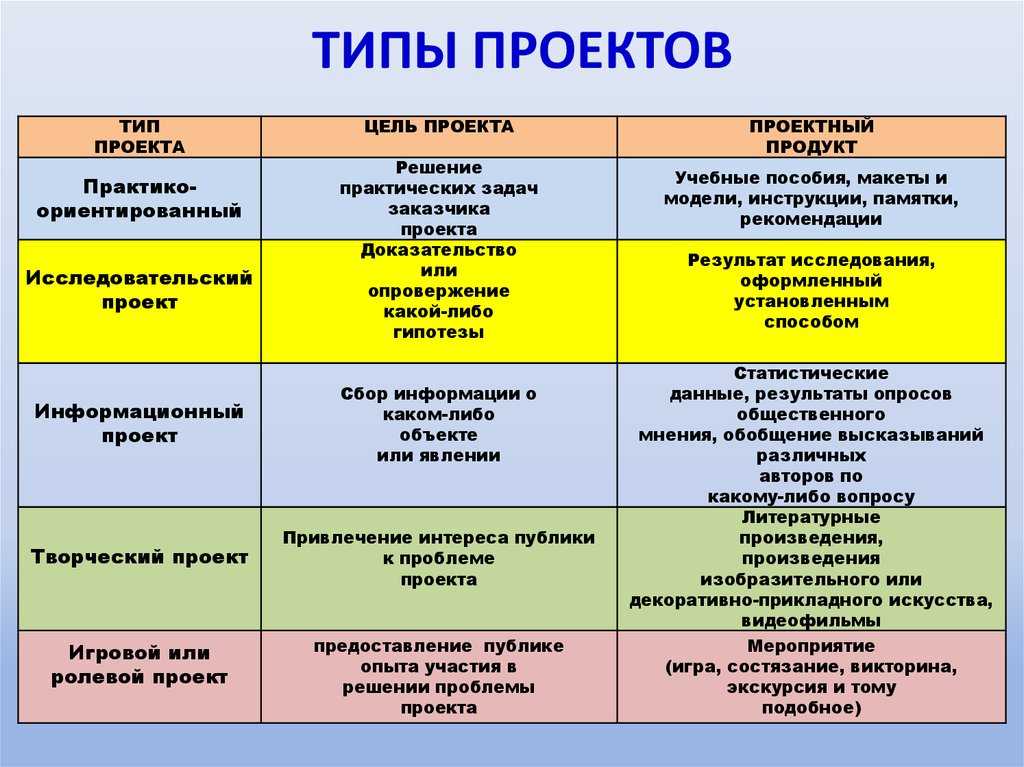 Но он не в полной мере оценил экспоненциальный рост. Поскольку на шахматной доске 64 клетки, мы можем использовать уравнение 2, чтобы определить, сколько зерен пшеницы потребуется для оплаты последней клетки ( R , возведенное в 64-ю степень, что составляет около 18 446 744 074 000 000 000 — действительно много пшеницы, уж точно больше, чем во всем королевстве). Эти примеры подчеркивают часто удивительный способ, которым экспоненциальный процесс может очень быстро привести к очень большим числам.

Эконометрика: определение, модели и методы

Что такое эконометрика?

Эконометрика — это использование статистических и математических моделей для разработки теорий или проверки существующих экономических гипотез, а также для прогнозирования будущих тенденций на основе исторических данных. Он подвергает реальные данные статистическим испытаниям, а затем сравнивает результаты с проверяемой теорией.

В зависимости от того, заинтересованы ли вы в проверке существующей теории или в использовании существующих данных для разработки новой гипотезы, эконометрику можно разделить на две основные категории: теоретическую и прикладную. Те, кто регулярно занимается этой практикой, широко известны как эконометристы.

Ключевые выводы

• Эконометрика — это использование статистических методов для разработки теорий или проверки существующих гипотез в экономике или финансах.
• Эконометрика опирается на такие методы, как модели регрессии и проверка нулевой гипотезы.
• Эконометрику также можно использовать для прогнозирования будущих экономических или финансовых тенденций.
• Как и в случае с другими статистическими инструментами, специалисты по эконометрике должны быть осторожны, чтобы не вывести причинно-следственную связь из статистической корреляции.
• Некоторые экономисты критикуют эконометрику за то, что она отдает предпочтение статистическим моделям, а не экономическим рассуждениям.

Смотреть сейчас: что такое эконометрика?

Понимание эконометрики

Эконометрика анализирует данные с использованием статистических методов для проверки или развития экономической теории. Эти методы основаны на статистических выводах для количественной оценки и анализа экономических теорий с использованием таких инструментов, как частотные распределения, вероятности и распределения вероятностей, статистические выводы, корреляционный анализ, простой и множественный регрессионный анализ, модели одновременных уравнений и методы временных рядов.

Эконометрика была разработана Лоуренсом Кляйном, Рагнаром Фришем и Саймоном Кузнецом. Все трое получили Нобелевскую премию по экономике за свой вклад. Сегодня он регулярно используется учеными, а также практиками, такими как трейдеры и аналитики с Уолл-стрит.

Примером применения эконометрики является изучение эффекта дохода с использованием наблюдаемых данных. Экономист может предположить, что по мере того, как человек увеличивает свой доход, его расходы также увеличиваются.

Если данные показывают, что такая связь присутствует, можно провести регрессионный анализ, чтобы понять силу связи между доходом и потреблением и выяснить, является ли эта связь статистически значимой, т. е. маловероятно, что она существует. только благодаря случайности.

Методы эконометрики

Первым шагом к эконометрической методологии является получение и анализ набора данных и определение конкретной гипотезы, объясняющей природу и форму набора. Этими данными могут быть, например, исторические цены фондового индекса, наблюдения, полученные в ходе обследования потребительских финансов, или уровни безработицы и инфляции в разных странах.

Если вас интересует взаимосвязь между годовым изменением цены S&P 500 и уровнем безработицы, вы должны собрать оба набора данных. Затем вы можете проверить идею о том, что более высокая безработица приводит к снижению цен на фондовом рынке. В этом примере цена на фондовом рынке будет зависимой переменной, а уровень безработицы — независимой или объясняющей переменной.

Наиболее распространенная зависимость является линейной, что означает, что любое изменение объясняющей переменной будет иметь положительную корреляцию с зависимой переменной. Эту взаимосвязь можно исследовать с помощью простой регрессионной модели, которая сводится к построению наиболее подходящей линии между двумя наборами данных и последующему тестированию, чтобы увидеть, насколько каждая точка данных в среднем удалена от этой линии.

Обратите внимание, что в вашем анализе может быть несколько объясняющих переменных, например, изменения ВВП и инфляции в дополнение к безработице для объяснения цен на фондовом рынке. Когда используется более одной независимой переменной, это называется множественной линейной регрессией. Это наиболее часто используемый инструмент в эконометрике.

Некоторые экономисты, в том числе Джон Мейнард Кейнс, критикуют эконометриков за то, что они слишком полагаются на статистические корреляции вместо экономического мышления.

Различные модели регрессии

Существует несколько различных моделей регрессии, которые оптимизируются в зависимости от характера анализируемых данных и типа задаваемого вопроса. Наиболее распространенным примером является обычная регрессия методом наименьших квадратов (OLS), которую можно проводить на нескольких типах перекрестных данных или данных временных рядов. Если вас интересует бинарный результат (да-нет) — например, вероятность того, что вас уволят с работы в зависимости от вашей продуктивности, — вы можете использовать логистическую регрессию или пробит-модель. Сегодня эконометристы имеют в своем распоряжении сотни моделей.

В настоящее время эконометрика проводится с использованием программных пакетов статистического анализа, разработанных для этих целей, таких как STATA, SPSS или R. Эти программные пакеты также могут легко проверять статистическую значимость, чтобы определить вероятность того, что корреляции могут возникнуть случайно. R-квадрат, t-тесты, p-значения и проверка нулевой гипотезы — все это методы, используемые эконометриками для оценки достоверности результатов их моделей.

Ограничения эконометрики

Эконометрику иногда критикуют за то, что она слишком сильно полагается на интерпретацию необработанных данных, не связывая их с устоявшейся экономической теорией или не ища причинно-следственных механизмов. Крайне важно, чтобы результаты, обнаруженные в данных, могли быть адекватно объяснены теорией, даже если это означает разработку вашей собственной теории лежащих в основе процессов.

Регрессионный анализ также не доказывает причинно-следственную связь, и только потому, что два набора данных показывают связь, она может быть ложной. Например, смертность от утопления в плавательных бассейнах увеличивается с ростом ВВП. Заставляет ли растущая экономика людей тонуть? Это маловероятно, но, возможно, больше людей покупают бассейны, когда экономика находится на подъеме. Эконометрика в основном занимается корреляционным анализом, и важно помнить, что корреляция не равна причинно-следственной связи.

Что такое оценщики в эконометрике?

Оценщик — это статистический показатель, который используется для оценки некоторого факта или измерения относительно большей совокупности. Оценщики часто используются в ситуациях, когда нецелесообразно измерять всю совокупность. Например, невозможно измерить точный уровень занятости в любое конкретное время, но можно оценить безработицу на основе случайно выбранной выборки населения.