Что такое система координат: СИСТЕМА КООРДИНАТ | это… Что такое СИСТЕМА КООРДИНАТ?
Содержание
Система координат | это… Что такое Система координат?
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.
В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.
В географии координаты — широта, долгота и высота над известным общим уровнем (например, океана). См. географические координаты.
В астрономии координаты — величины, при помощи которых определяется положение звезды, например, прямое восхождение и склонение.
Небесные координаты — числа, с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой систему полярных координат на сфере с соответствующим образом выбранным полюсом. Систему небесных координат задают большим кругом небесной сферы (или его полюсом, отстоящим на 90° от любой точки этого круга) с указанием на нём начальной точки отсчёта одной из координат. В зависимости от выбора этого круга системы небесных координат называлась горизонтальной, экваториальной, эклиптической и галактической.
Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).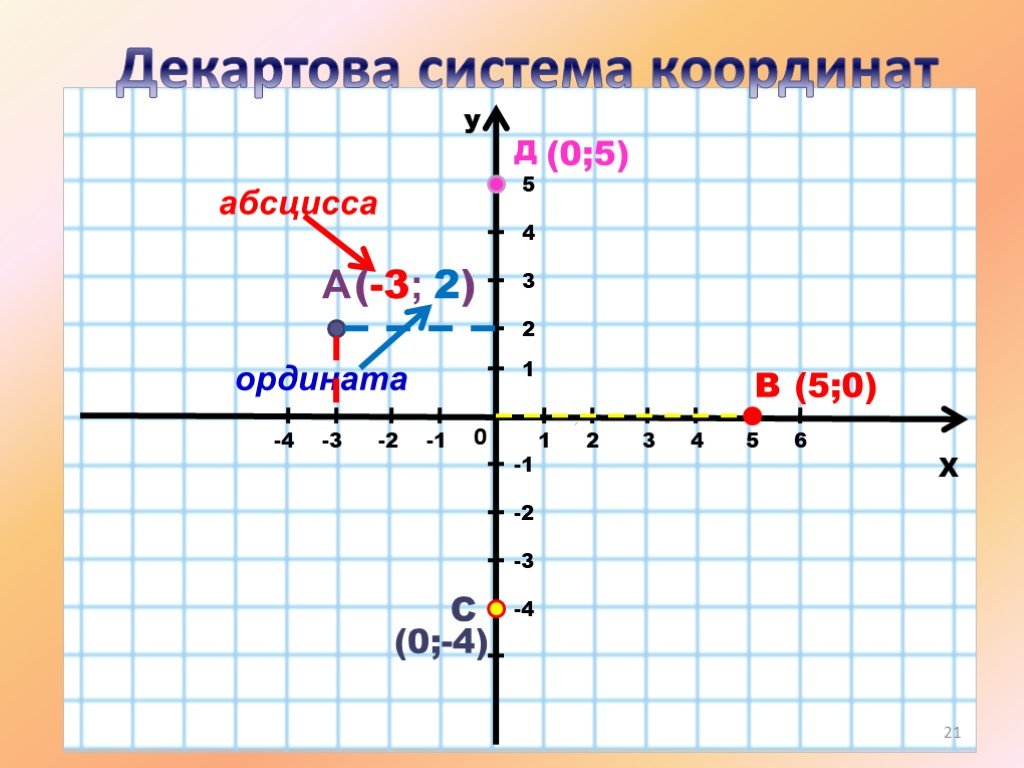
Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.
Содержание
|
Список наиболее распространённых систем координат
- Аффинная (косоугольная) система координат
- Барицентрические координаты
- Биангулярные координаты
- Биполярные координаты
- Бицентрические координаты
- Бицилиндрические координаты
- Конические координаты
- Координаты Риндлера — в пространстве Минковского
- Параболические координаты
- Полярная система координат
- Проективные координаты
- Прямоугольная (Декартова) система координат
- Сферическая система координат
- Тороидальная система координат
- Трилинейные координаты
- Цилиндрическая система координат
- Цилиндрические параболические координаты
- Эллипсоидальные координаты (эллиптические координаты)
Основные системы
В этом разделе даются разъяснения к наиболее употребляемым системам координат в элементарной математике.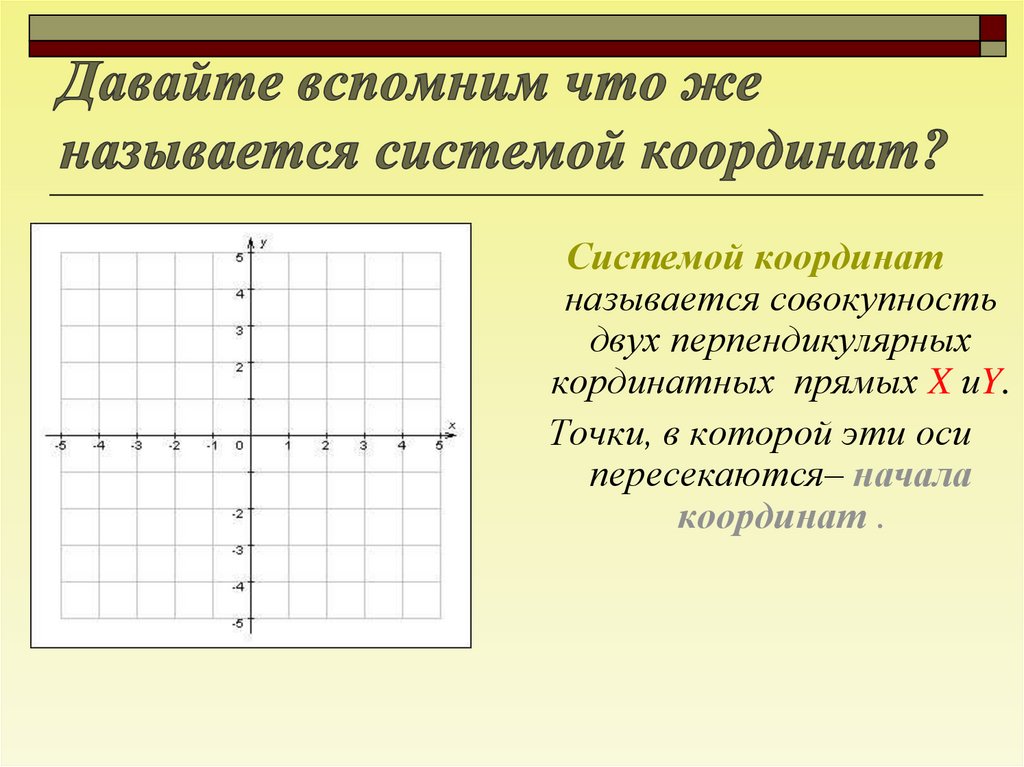
Декартовы координаты
Основная статья: Прямоугольная система координат
Расположение точки P на плоскости определяется декартовыми координатами с помощью пары чисел :
- — расстояние от точки P до оси y с учетом знака
- — расстояние от точки P до оси x с учетом знака
В пространстве же необходимо уже 3 координаты :
- — расстояние от точки P до плоскости yz
- — расстояние от точки P до плоскости xz
- — расстояние от точки P до плоскости xy
Полярные координаты
Полярные координаты.
Основная статья: Полярная система координат
В полярной системе координат положение точки определяется расстояние до центра координат и углом радиус-вектора с осью Ox.
Термин «полярные координаты» используется только на плоскости, в пространстве применяются цилиндрические и сферические системы координат.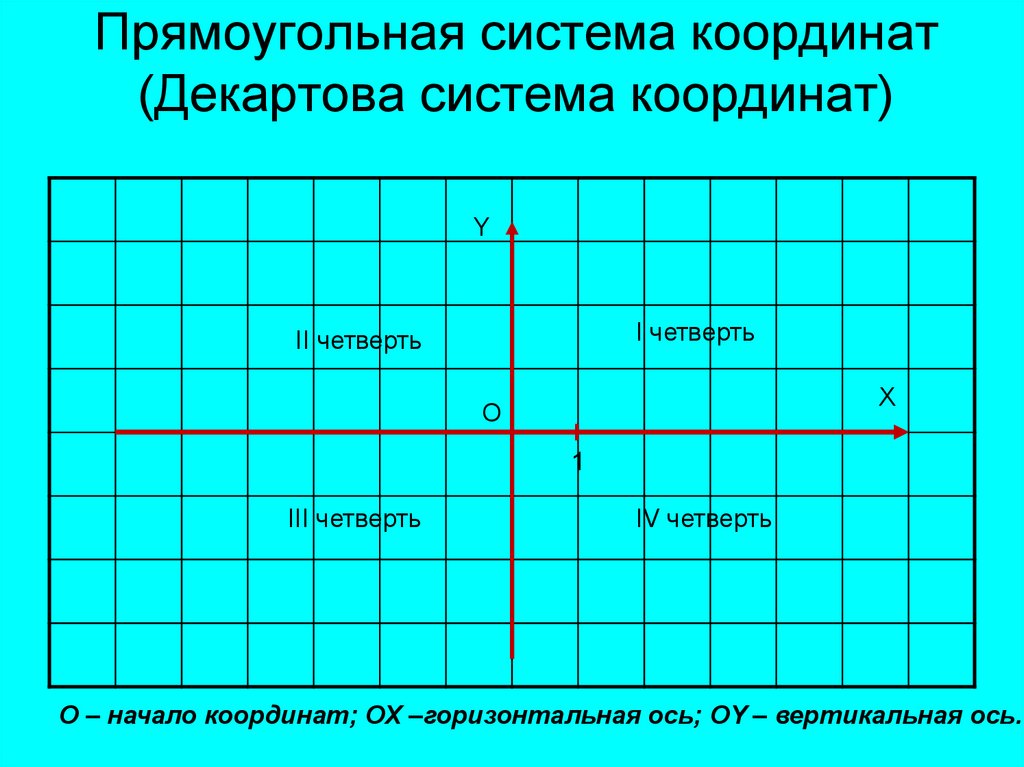
Цилиндрические координаты
Цилиндрические координаты.
Основная статья: Цилиндрическая система координат
Цилиндрические координаты — трехмерный аналог полярных, в котором точка P представляется трехкомпонентным кортежем . В терминах декартовой системы координат,
- (радиус) — расстояние от оси z к точке P,
- (азимут или долгота) — угол между положительной («плюсовой») частью оси x и прямой линии, мысленно проведённой от полюса до точки P, спроектирован на xy-плоскость
- (высота) — расстояние (с учетом знака) от xy-плоскости до точки P.
- Примечание: в литературе можно встретить пометку z для h; это не принципиально, но нужно следить, какие отметки применяются.
Полярные координаты имеют один недостаток: значение θ теряет смысл, если r = 0.
Цилиндрические координаты полезны для изучения систем, симметричных вокруг некой оси. Например, длинный цилиндр в декартовых координатах имеет уравнение , тогда как в цилиндрических оно выглядит как r = c
Сферические координаты
Сферические координаты.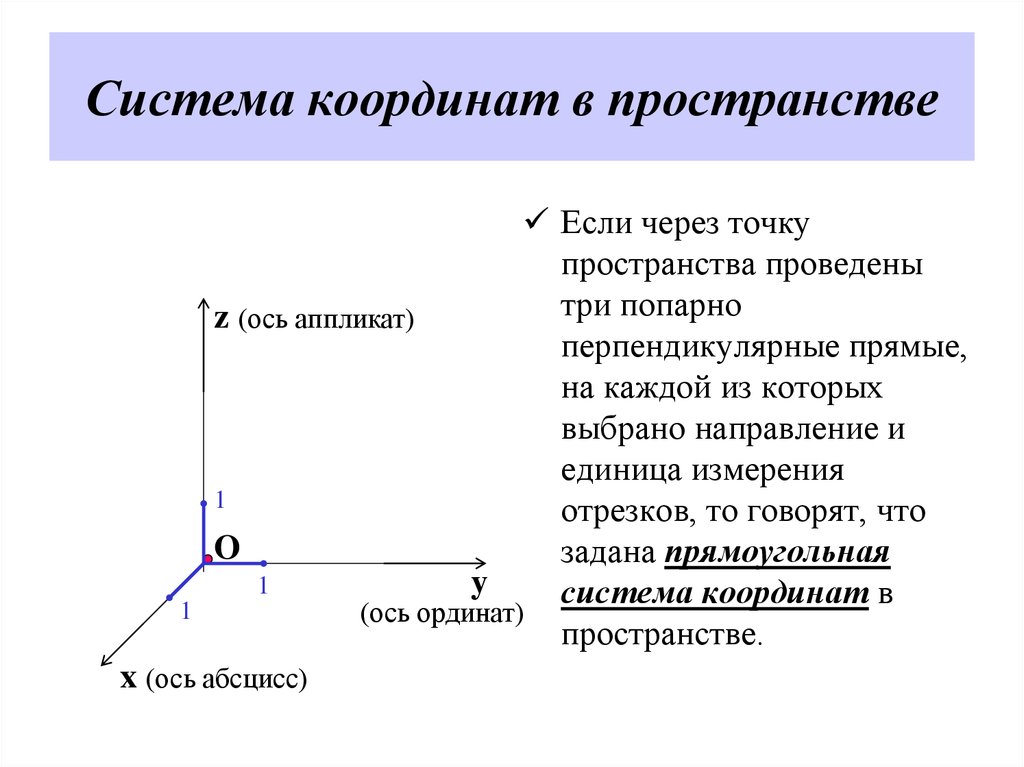
Основная статья: Сферическая система координат
Сферические координаты — трехмерный аналог полярных
Обозначения, принятые в Америке
В сферической системе координат, расположение точки P определяется тремя компонентами: . В терминах декартовой системы координат,
- (радиус) — это расстояние от точки Р до полюса,
- (широта или полярный угол) — угол между z-осью и прямой, проведённой из полюса до точки P
- (азимут или долгота) — угол между положительной («плюсовой» x-осью и проекцией прямой, проведённой из полюса до точки P на xy-плоскость.
- Примечание: в литературе можно встретить пометку φ или θ, а также r для ρ;
Сферическая система координат также имеет недостаток: φ теряет смысл если ρ = 0, также и θ теряет смысл, если ρ = 0 или φ = 0 или φ = 180°.
Для построения точки по её сферическими координатами, нужно: от полюса отложить отрезок, равный ρ вдоль положительной z-оси, вернуть его на угол φ вокруг оси y в направлении положительной x-оси, и вернуть на угол θ вокруг z-оси в направлении положительной y-оси.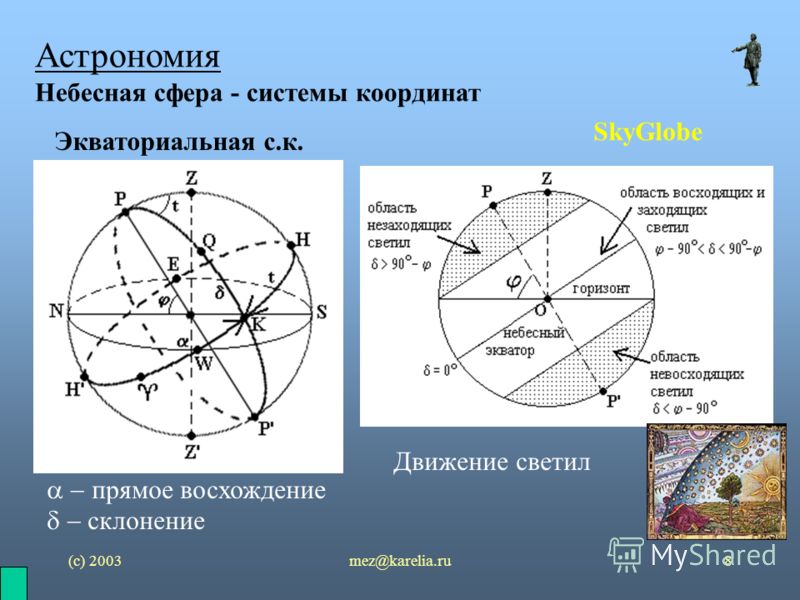
Сферические координаты полезны при изучении систем, симметричных вокруг точки. Так, уравнение сферы в декартовых координатах выглядит как , тогда как в сферических становится намного проще: .
Европейские обозначения
В Европе принято использовать другие обозначения. Положение точки задаётся числами: , Где r — расстояние от точки до начала координат, — полярный угол, который изменяется в пределах от 0 до π, — Азимутальный угол, который изменяется в пределах от 0 до 2π. То есть, в европейской системе, которая применяется также и в России, обозначения для углов переставлены по сравнению с американской.
Переход из одной системы координат в другую
Декартовы и полярные
где u0 — функция Хевисайда с , а sgn — функция signum . Здесь функции u0 и sgn используются как «логические» переключатели, аналогичные по значению операторам «если .. то» (if…else) в языках программирования. Некоторые языки программирования имеют специальную функцию atan2 (y, x), которая находит правильный θ в необходимом квадранте, определённом x и y.
Некоторые языки программирования имеют специальную функцию atan2 (y, x), которая находит правильный θ в необходимом квадранте, определённом x и y.
Декартовы и цилиндрические
Декартовы и сферические
Уравнения для американских обозначений
Цилиндрические и сферические
См. также
- Системы координат в элементарной математике
- Галилеевы координаты
- Гауссовы координаты
- Нормальные координаты
- Римановы координаты
- Начало координат, координатная ось, орт
- Локальный стандарт покоя (начало координат в астрономии)
- Главноортодромическая система координат
- Размерность пространства
Литература
- Гельфанд И.
 М., Глаголева Е. Г., Кириллов А. А. Метод координат. Издание пятое, стереотипное. Серия: Библиотечка физико-математической школы. Математика. Выпуск 1. М.: Наука, 1973.
М., Глаголева Е. Г., Кириллов А. А. Метод координат. Издание пятое, стереотипное. Серия: Библиотечка физико-математической школы. Математика. Выпуск 1. М.: Наука, 1973.
Ссылки
- Факультативное занятие по математике на тему: «Разные системы координат»
Системы координат в геодезии — какие бывают и как используются?
В данной статье мы разбираем основные вопросы по геодезии. Что такое системы координат, какие виды СК выделяют, какие из них используются на практике и для чего. А также, отвечаем на вопрос, почему мы предоставляем поправки в международной системе координат.
Содержание статьи:
- Что такое система координат?
- Какие бывают системы координат?
2.1 Полярная система координат (полярные координаты)
2.2 Плоская прямоугольная (прямолинейная система координат)
2.3 Прямоугольная пространственная система координат - Земные и референцные системы координат в геодезии
3.1 Земная система координат
3. 2 Референцная система координат
2 Референцная система координат - Что такое геодезическая система координат?
- Системы координат, используемые на практике
5.1 Система координат WGS-84
5.2 Система координат ПЗ-90.11
5.3 Система координат ГСК-2011
5.4 Система координат МСК
5.5 Архивные системы координат - Какие бывают системы отсчета высот?
- Почему мы предоставляем поправки в международной системе координат?
- Почему я не получаю фиксированного решения?
Надеемся, этот материал поможет получить ответы на интересующие вопросы.
Что такое система координат?
Система координат (СК) — это набор математических правил, описывающих, как координаты должны быть соотнесены с точками пространства.
Иными словами, это совокупность условий, определяющих положение и перемещение точки или объекта на прямой, на плоскости, в пространстве с помощью чисел или других символов.
Совокупность чисел, определяющих положение точки, называется координатами этой точки.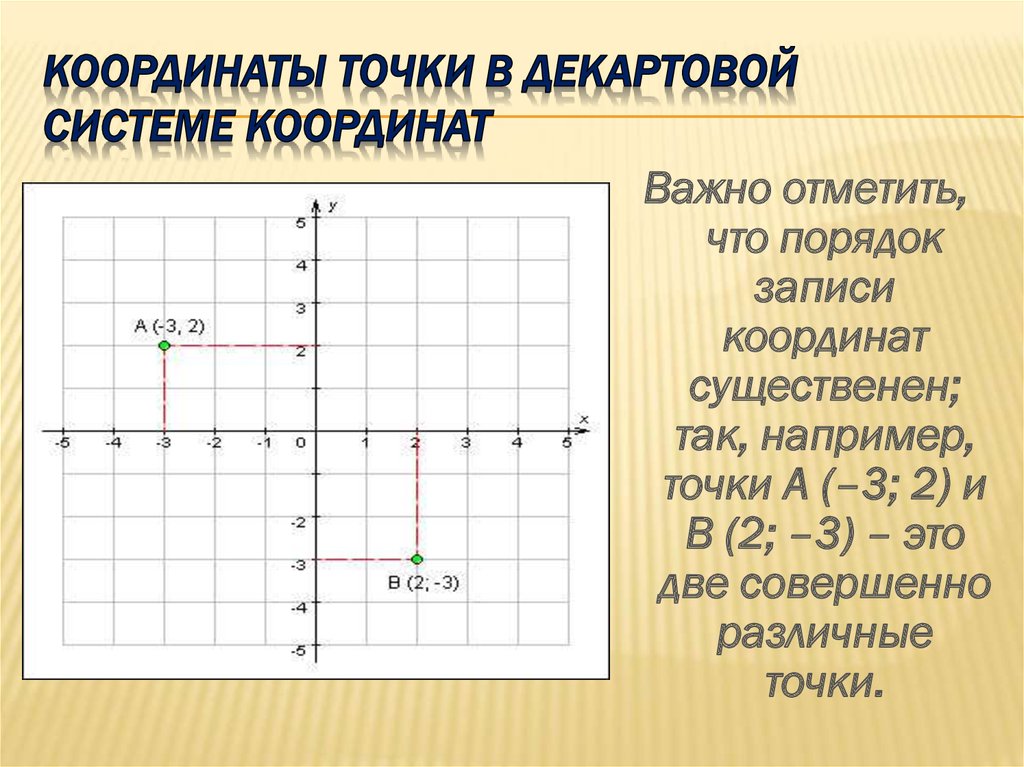
Какие бывают системы координат?
Существуют разные геодезические системы координат, они используются в зависимости от масштаба, в котором необходимо произвести расчет расположения объекта на Земле.
В рамках данной статьи, разберемся, какие именно бывают системы координат и как используются на практике в геодезии.
Полярная система координат (полярные координаты)
Полярная система координат — это система координат, положение точки в которой задается расстоянием и направлением от ее начала.
Двумерная полярная система координат может быть задана на плоскости, поверхности сферы или эллипсоида.
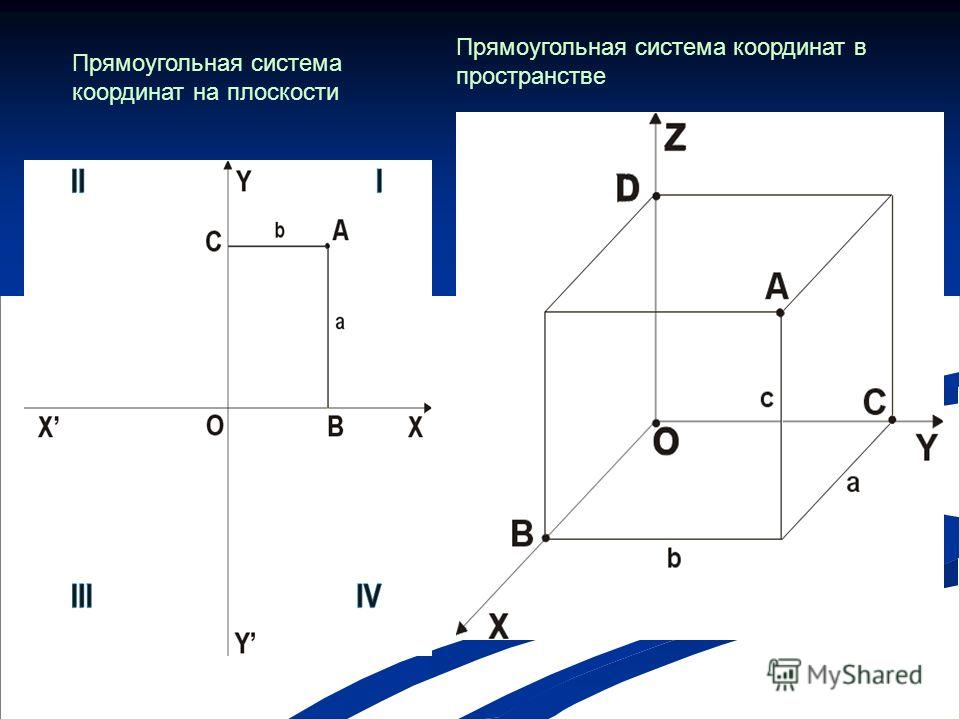
Плоская прямоугольная (прямолинейная система координат)
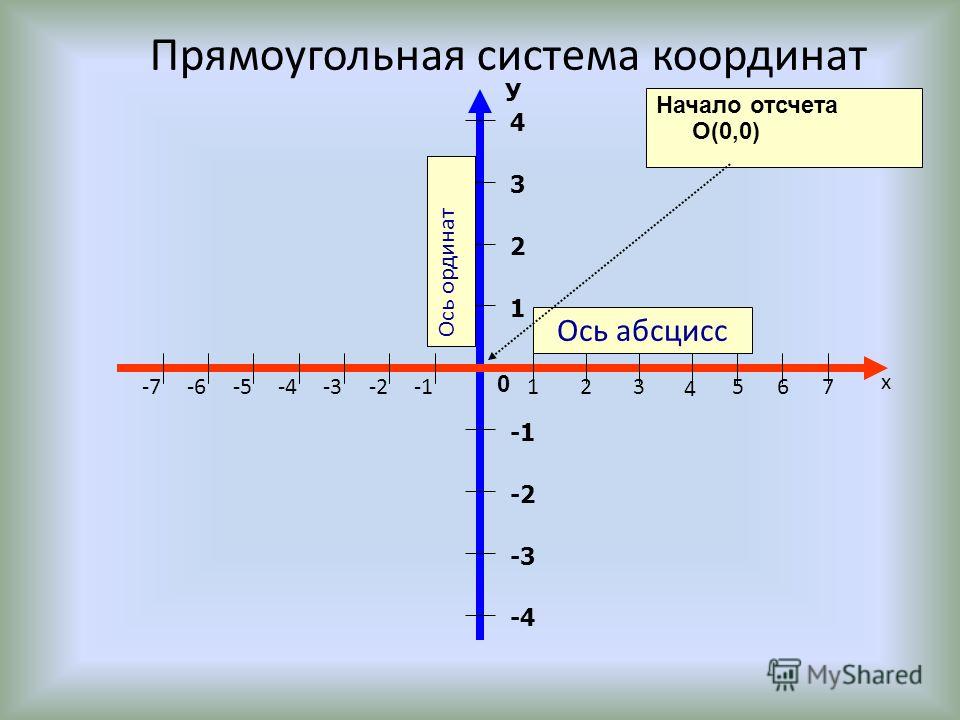
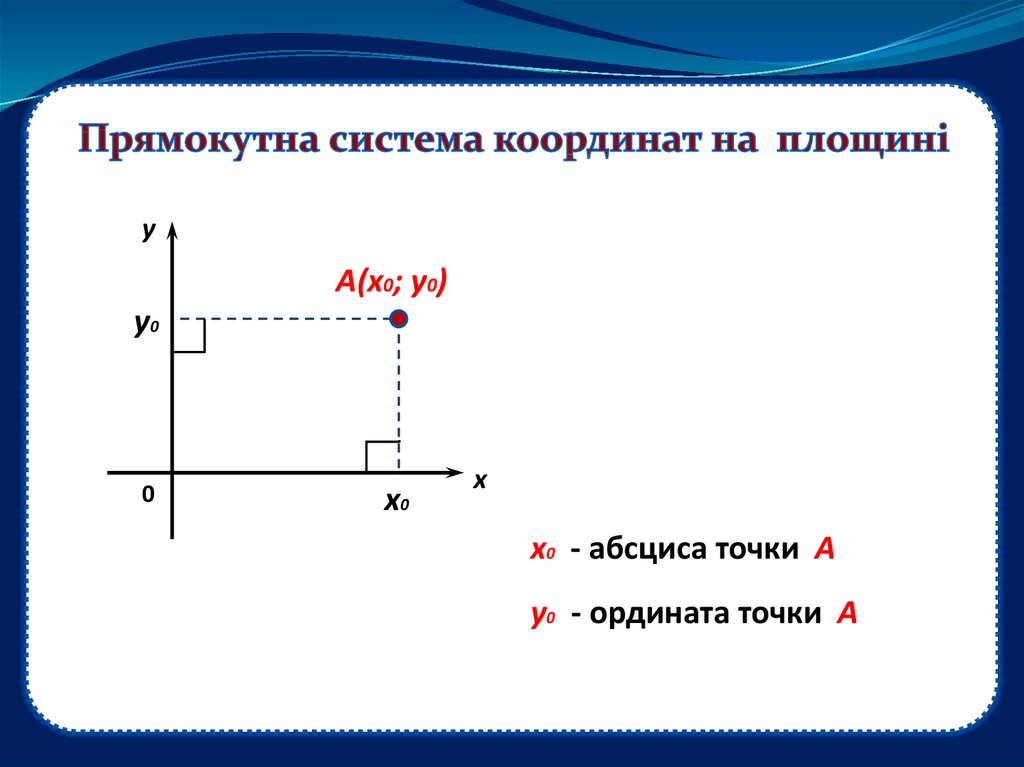
Плоская прямоугольная (прямолинейная) система координат — это система координат, определяющая положение точек по отношению к взаимно перпендикулярным осям, исходящим из ее начала.
Координаты точки в данной системе координат представлены в виде плоских прямоугольных координат x и y.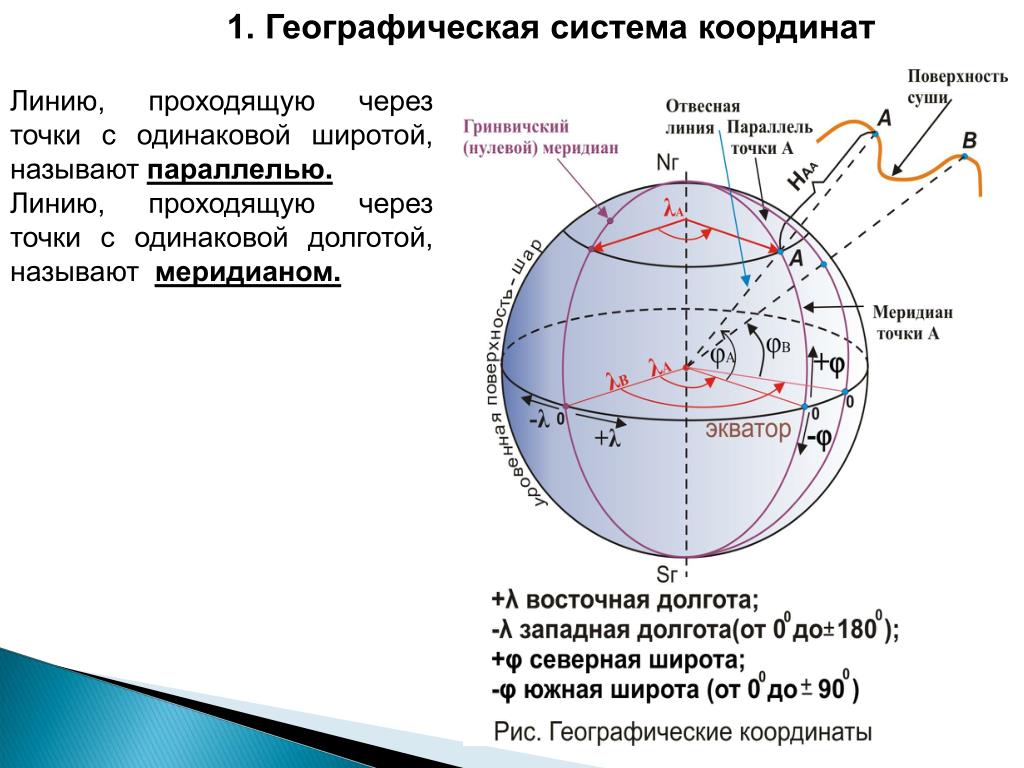 В геодезии — это координаты на плоскости, на которой отображена поверхность земного эллипсоида в заданной картографической проекции.
В геодезии — это координаты на плоскости, на которой отображена поверхность земного эллипсоида в заданной картографической проекции.
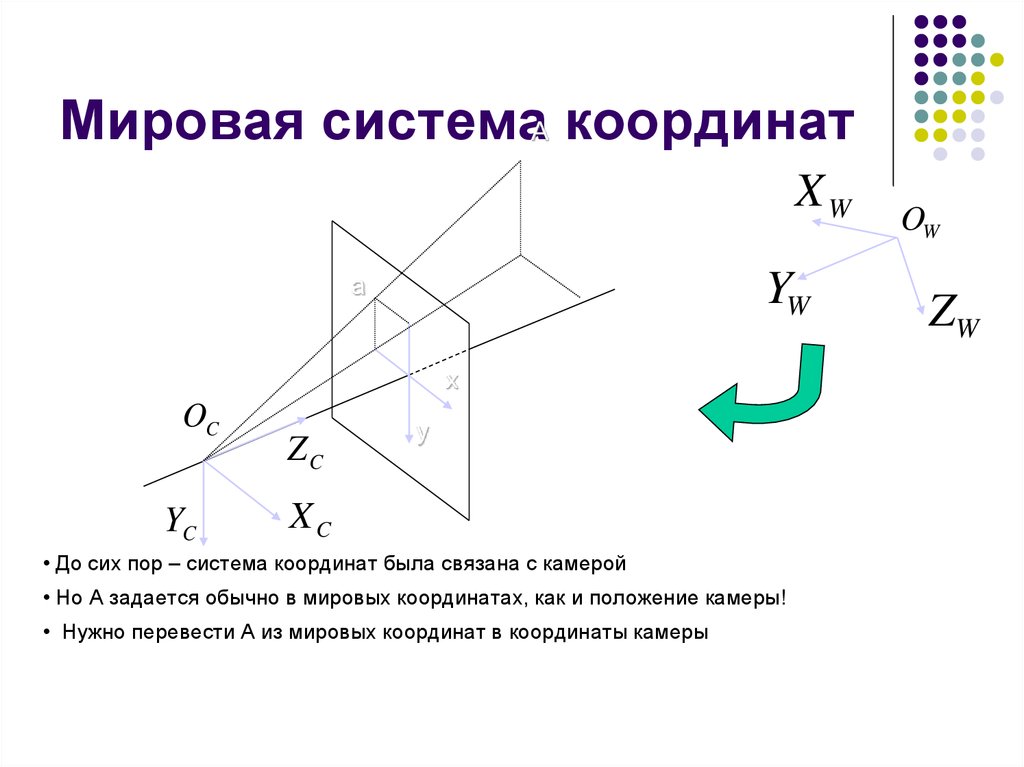
Прямоугольная пространственная система координат
Прямоугольная пространственная система координат — это система трехмерных линейных прямоугольных координат по координатным осям Х, У, Z координат, у которой оси Х и У лежат в экваториальной плоскости, ось Х направлена к начальному меридиану, ось Z направлена на север, орты образуют правую тройку векторов, а начало координат совпадает с центром земного эллипсоида.
Координаты точки в пространственной системе координат представлены в виде геодезических (эллипсоидальных) координатах или в прямоугольных пространственных координатах.
Земные и референцные системы координат
Помимо вышеупомянутых, различают земные (общеземные) и референцные системы координат. Разбираемся, чем они отличаются.
Что такое земная система координат в геодезии?
Земная система координат — это пространственная система координат, предназначенная для количественного описания положения и движения объектов, находящихся на поверхности Земли и в околоземном пространстве.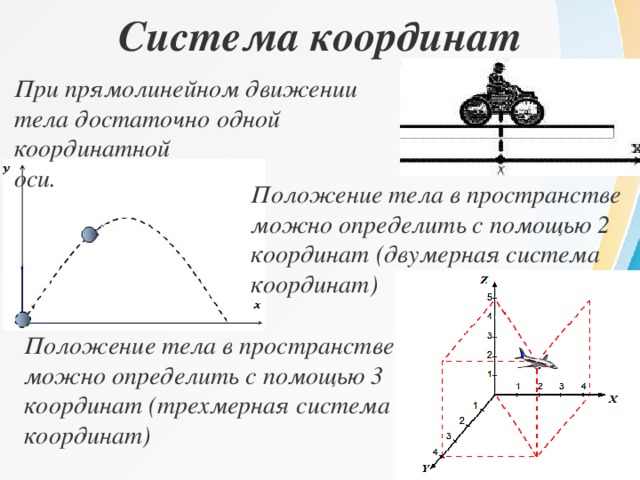
Что такое референцная система координат в геодезии?
Референцная система координат — это система координат, созданная с целью обеспечения геодезических и картографических работ на конкретной территории. К ним можно отнести местные и условные системы координат.
Что такое геодезическая система координат?
Геодезическая система координат — это система координат, которая используется для определения точного местоположения объекта на земном шаре.
За земной шар, для удобства проведения математических расчетов в инженерной геодезии, принимают шар с R=6371.11 км. Объем земного шара при этом равен объему земного эллипсоида.
Что такое геодезические координаты?
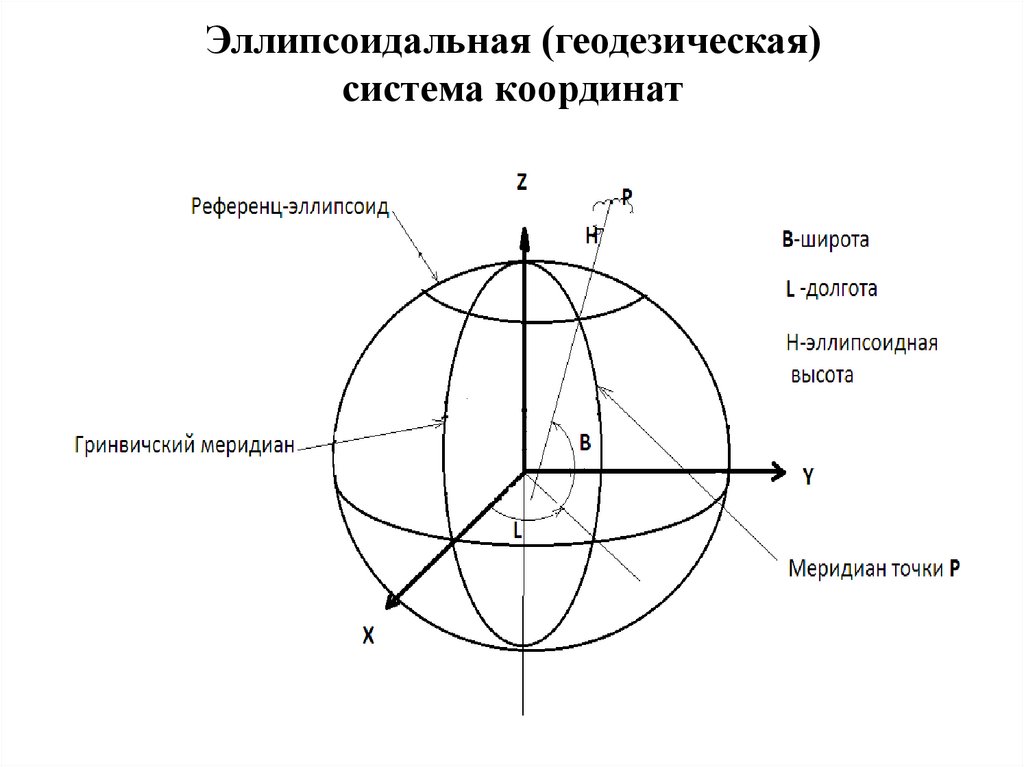
Геодезические координаты — это величины, два из которых (геодезическая широта B и геодезическая долгота L) характеризуют направление нормали к поверхности отсчетного эллипсоида в данной точке пространства относительно плоскостей его экватора и начального меридиана, а третий (геодезическая высота H) представляет собой высоту точки над поверхностью отсчетного эллипсоида.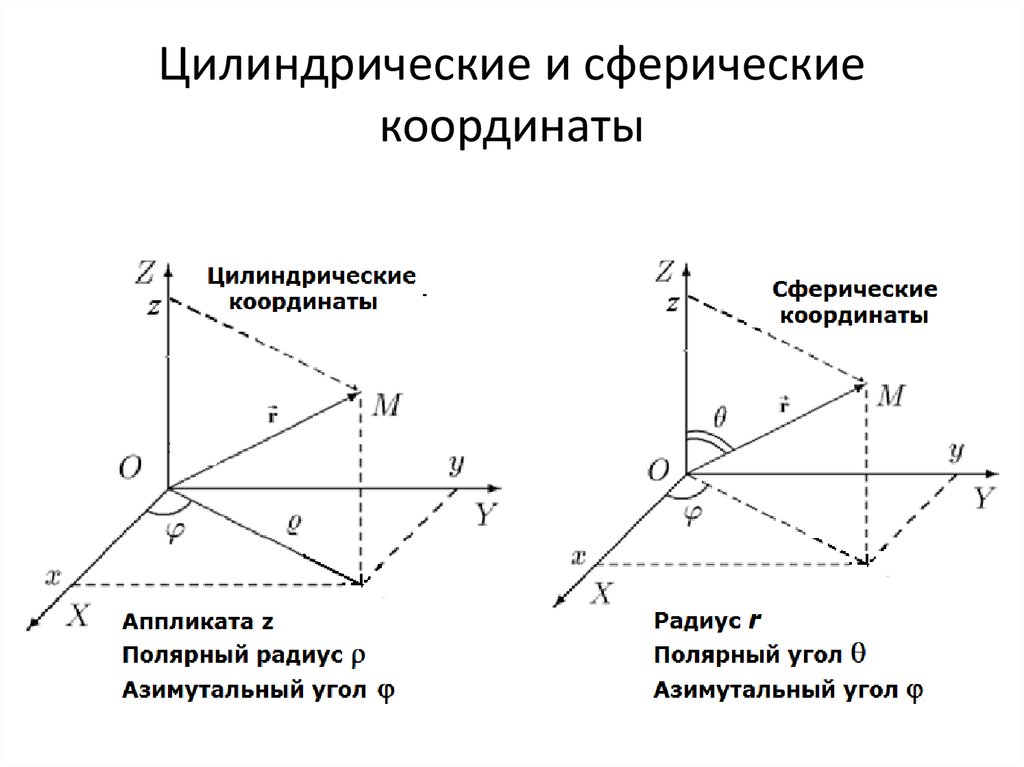
В земных системах координат центр координат совпадает с центром масс Земли, поэтому прямоугольные пространственные координаты называют геоцентрическими координатами.
Системы координат также подразделяют на государственные, местные, локальные и международные.
СК, используемые на практике
Практическими реализациями пространственной геоцентрической земной системы координат являются системы координат WGS-84, ПЗ-90.11 и ГСК-2011.
Система координат WGS-84
WGS-84 (World Geodetic System (Всемирная геодезическая система координат)) – это система геодезических параметров Земли 1984 года, используемая в GPS, в число которых входит система геоцентрических координат).
Система координат ПЗ-90.11
ПЗ-90.11 (общеземная геоцентрическая система координат «Параметры Земли 1990 года») — это государственная система координат, используемая в ГЛОНАСС.
ПЗ-90.11 была установлена постановлением Правительства РФ от 24 ноября 2016 года №1240 для использования в целях геодезического обеспечения орбитальных полетов, решения навигационных задач и выполнения геодезических и картографических работ в интересах обороны Российской Федерации.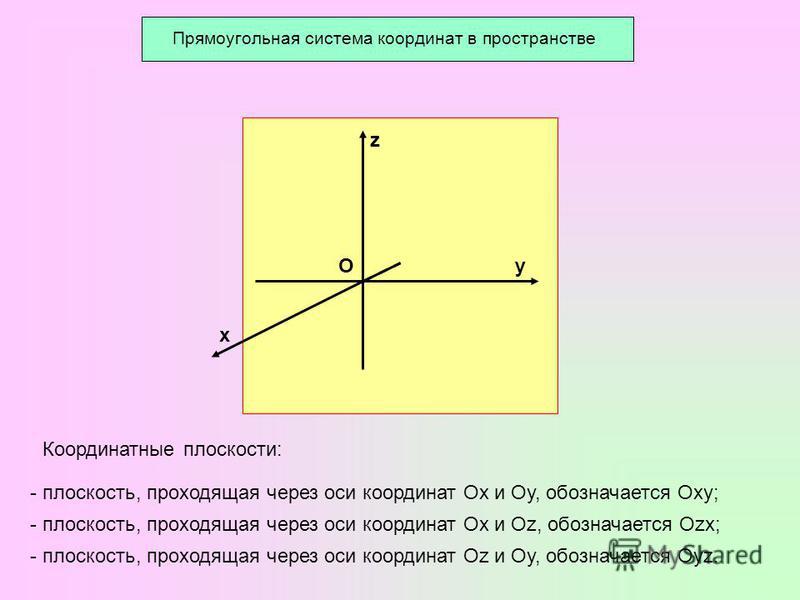
Система координат ГСК-2011
ГСК-2011 (геодезическая система координат 2011 года) – это государственная система координат, установленная постановлением Правительства РФ от 24 ноября 2016 года №1240 для использования при осуществлении геодезических и картографических работ на территории Российской Федерации.
Система координат МСК
МСК – это местная система координат субъекта Российской Федерации, установленная для целей обеспечения проведения геодезических и картографических работ при осуществлении градостроительной и кадастровой деятельности, землеустройства, недропользования и иной деятельности.
Каждый субъект имеет свою МСК с номером данного субъекта, например, местная система координат Московской области именуется МСК-50.
Архивные системы координат
Существуют архивные системы координат, которые в настоящее время не используются (не действуют).
Среди них можно выделить:
- СК-42 – система координат 1942 года, введенная постановлением Совета Министров СССР от 7 апреля 1946 года №760 в качестве единой государственной системы координат при выполнении геодезических и картографических работ.
- СК-63 – система координат 1963 года, предназначенная для создания топографических и специальных карт гражданского применения, а также для решения народнохозяйственных задач на территории Советского Союза. Отменена Постановлением ЦК КПСС и СМ СССР от 25 марта 1987.
- СК-95 – система координат 1995 года, установленная постановлением Правительства Российской Федерации от 28 июля 2000 года №568 в качестве единой государственной системы координат при выполнении геодезических и картографических работ.
Какие бывают системы отсчета высот?
Высоты в геодезии могут быть представлены в виде геодезических, ортометрических и нормальных и высот. Высоты также могут быть представлены в условной системе высот.
Основные системы отсчета высот:
- Геодезическая высота – высота точки над поверхностью земного эллипсоида, отсчитываемая по нормали;
- Ортометрическая высота – высота точки над поверхностью геоида, отсчитываемая по отвесной линии;
- Нормальная высота – высота точки над поверхностью квазигеоида, отсчитывается по нормали.
 Нормальной высотой является величина, численно равная отношению геопотенциальной величины в данной точке к среднему значению нормальной силы тяжести Земли по отрезку, отложенному от поверхности земного эллипсоида
Нормальной высотой является величина, численно равная отношению геопотенциальной величины в данной точке к среднему значению нормальной силы тяжести Земли по отрезку, отложенному от поверхности земного эллипсоида
На территории Российской Федерации применяется Балтийская система высот 1977 года, которая является реализацией системы нормальных высот.
Отсчет высот в Балтийской системе высот 1977 года ведется от нуля Кронштадтского футштока, укрепленного в устое моста через обводной канал в г. Кронштадте.
Почему мы предоставляем поправки в международной системе координат?
Поскольку ГНСС работают в реализациях земной геоцентрической системы координат, таких как WGS-84 и ПЗ-90.11, то первоначально все спутниковые определения с использованием ГНСС выполняются в этих системах координат.
В ГНСС аппаратуре и программном обеспечении все результаты (координаты, скорости, ускорения) вначале приводятся в WGS-84, которые можно представить в любой другой системе координат путем математических преобразований.
Координаты в пространственных земных системах WGS-84, ПЗ-90.11 или ГСК-2011 с точностью 1 метр практически совпадают, поэтому для спутниковых определений с такой точностью не имеет значения в какой из реализаций системы координат они представлены.
Для спутниковых определений с высокой точностью мы предоставляем дифференциальные поправки, которые применяются к измеряемым величинам в процессе спутниковых определений. Дифференциальные поправки позволяют определить пространственные координаты относительно спутниковых базовых станций с заданными координатами.
Поскольку в нашей сети координаты всех станций определены в международной системе координат WGS-84, координаты определяемых вами точек также первоначально представлены в WGS-84. Но, как уже было сказано выше, они могут быть преобразованы в любую систему координат по известным параметрам преобразования.
Почему я не получаю фиксированного решения?
Такая ситуация может возникнуть по нескольким причинам: Например, плохая связь. Полная шкала сигнала сотового оператора не означает хороший и стабильный интернет. Посмотрите на ровере, в свойствах подключения к RTK параметр «Возраст поправок». Он должен быть равен 1 сек. Это означает, что вы получаете поправку каждую секунду. Если возраст поправок более 2 сек — это говорит о плохой связи и задержках в передачи данных. При плохой связи ровер будет фиксироваться и тут же терять решение.
Полная шкала сигнала сотового оператора не означает хороший и стабильный интернет. Посмотрите на ровере, в свойствах подключения к RTK параметр «Возраст поправок». Он должен быть равен 1 сек. Это означает, что вы получаете поправку каждую секунду. Если возраст поправок более 2 сек — это говорит о плохой связи и задержках в передачи данных. При плохой связи ровер будет фиксироваться и тут же терять решение.
Другая причина — это помехи, которые заглушают часть частот, на которых передаются сигналы GPS/ГЛОНАСС. Если вы находитесь в чистом поле, но фиксированного решения нет, то возможно, помехи создаются линиями электропередач, подземными кабелями или работающей военной техникой, расположенной от вас в нескольких км. Например база или ваш ровер может принимать сигнал с 2 из 8 спутников GPS или ГЛОНАСС. В такой ситуации фиксированного решения тоже не будет.
систем координат: в чем разница?
Системы координат являются фундаментальными знаниями для специалиста по ГИС. Но столько непонятных терминов!
Но столько непонятных терминов!
Не можете вспомнить разницу между этой геодезией и этой? Я составил список вещей, которые меня в тот или иной момент смущали при работе с системами координат. Надеюсь, эти объяснения помогут прояснить ситуацию и для вас.
В чем разница между:
- GCS и PCS?
- Датам и географическая система координат?
- Проекция и система координат проекции?
- WKT и WKID?
- Инструмент «Определить проекцию» и инструмент «Проект»?
- Проекция на лету и географические преобразования?
- Пространственная привязка и система координат?
В чем разница между GCS и PCS?
Географическая система координат (GCS) — это система координат, определяющая расположение объектов на модели Земли. Он имеет форму шара — сферический. Его единицы угловые, обычно градусы.
Система координат проекции (PCS) является плоской. Он содержит GCS, но преобразует эту GCS в плоскую поверхность, используя математику (алгоритм проецирования) и другие параметры. Его единицы линейны, чаще всего в метрах.
Его единицы линейны, чаще всего в метрах.
GCS необходима для того, чтобы данные знали, где именно на земной поверхности они расположены. PCS необходим для отображения данных на плоской карте.
Дополнительные сведения см. в разделе Географические и проекционные системы координат.
В чем разница между датумом и географической системой координат?
Датам — это один параметр в географической системе координат (ГСК).
Датам является частью GCS, которая определяет, какая модель (сфероид) используется для представления земной поверхности и где она расположена относительно поверхности. Поскольку земная поверхность не является идеально гладкой или круглой, существует множество различных датумов, предназначенных для разных частей мира.
A GCS — это полное определение того, как привязать значения координат к реальным местоположениям на Земле. В дополнение к системе отсчета GCS включает в себя нулевой меридиан (который указывает положение 0 ° долготы) и угловую единицу (часто градусы).
База включает сфероид, который определяется своей большой полуосью, малой полуосью и значениями обратного сглаживания.
В чем разница между проекцией и системой координат проекции?
Проекция — это один параметр в системе координат проекции (PCS).
Проекция — это математический алгоритм, который определяет, как представить круглую землю на плоской карте. Вы можете увидеть все проекции, доступные в ArcGIS, в списке поддерживаемых картографических проекций.
A PCS — это полное определение того, как конкретная модель круглой земли проецируется на плоскую карту. В дополнение к проекции PCS включает в себя географическую систему координат (которая определяет модель Земли), единицу измерения (часто метры) и набор значений параметров, которые варьируются в зависимости от проекции (ложный восток, центральный меридиан, стандартная параллель, и так далее). Их можно использовать для центрирования PCS в разных частях мира.
Как следует из названия, PCS — это система координат. Проекция — это не система координат; это алгоритм, который используется для создания PCS.
В чем разница между WKT и WKID?
Оба эти средства идентификации систем координат, так что вы можете быть уверены, что используете те же параметры, что и кто-то другой.
Общеизвестный текст (WKT) — это строка, определяющая все необходимые параметры системы координат. Сохраните файл проекции (.prj) любой системы координат и откройте его в текстовом редакторе, чтобы увидеть его WKT.
Общеизвестный идентификатор (WKID) — это уникальный номер, присвоенный системе координат. Вы можете найти WKID в окне «Сведения о системе координат». Как только вы узнаете это число, это удобный способ поиска системы координат позже.
Авторитет WKID будет либо EPSG (European Petroleum Survey Group), либо Esri, но эти номера не пересекаются, поэтому нет необходимости беспокоиться о том, какой орган определил идентификатор.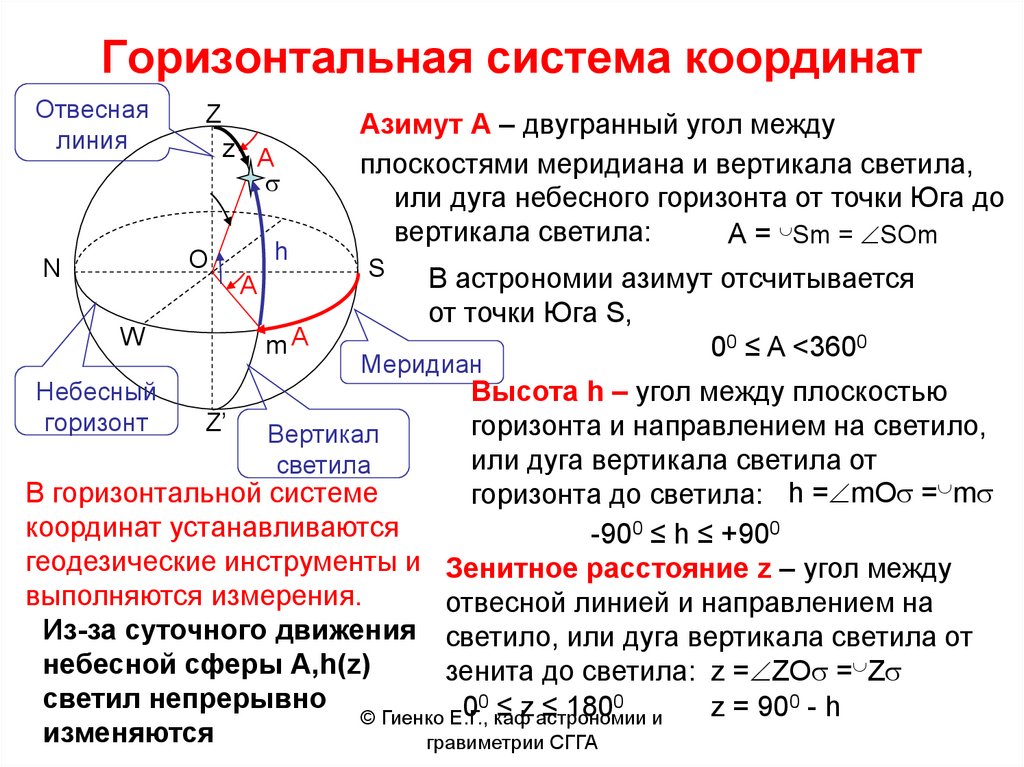
В чем разница между инструментом «Определить проекцию» и инструментом «Проект»?
Инструмент Определить проекцию используется в основном, когда данные имеют неизвестную систему координат. Он переназначает информацию о системе координат в метаданных. Это не изменит фактические значения координат.
Инструмент Project преобразует все координаты из одной системы координат в другую. Он также обновляет информацию метаданных.
Дополнительные сведения см. в разделе Определение проекции или проекта?
В чем разница между проекцией на лету и географическими преобразованиями?
Географические преобразования являются частью процесса прогнозирования на лету.
Проекция на лету — это то, что делает ArcGIS для разрешения конфликтов, когда ваши данные находятся в системе координат, отличной от вашей карты. Если бы у вас не было проекций «на лету», вы не смогли бы рисовать данные до того, как сначала преобразовали их в ту же систему координат, что и карта.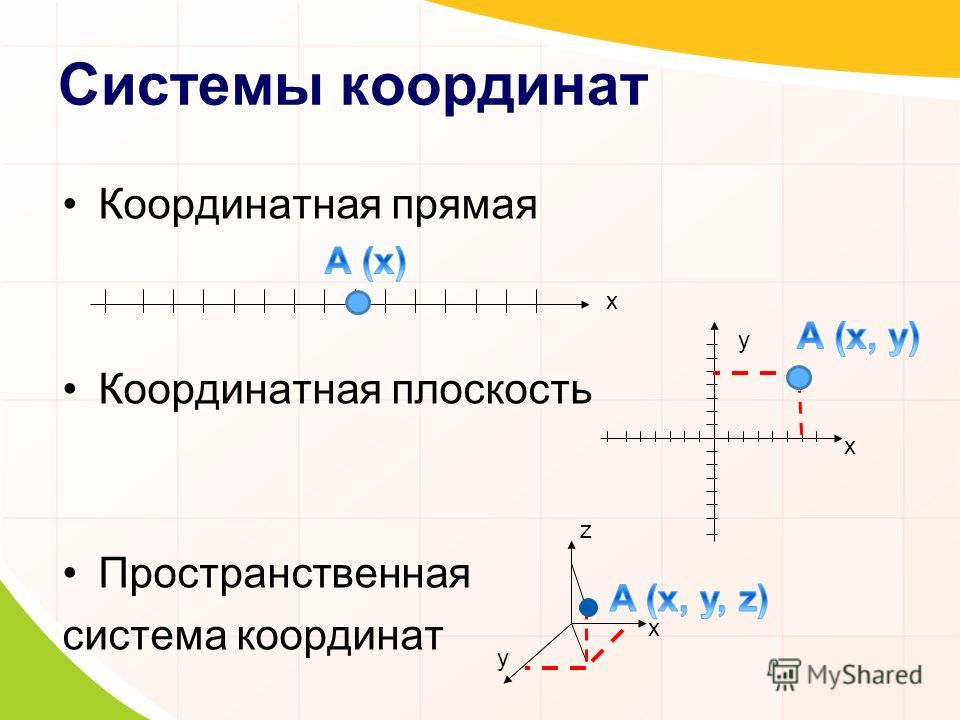
Всякий раз, когда проецирование на лету включает преобразование между географическими системами координат, процесс будет включать географических преобразований . Это вычисления, которые преобразуют координаты из одной ГСК в другую. Их иногда называют преобразованиями данных .
Вы можете выбрать, какое преобразование использовать. Если ваши данные используют другую GCS, чем ваша карта, и вы не используете географическое преобразование, данные будут отображаться не в том месте.
Чтобы узнать больше, прочитайте проекцию на лету и географические преобразования.
В чем разница между пространственной привязкой и системой координат?
Нет ни одного. По крайней мере, не в продуктах Esri. Термины используются взаимозаменяемо.
Вы можете посмотреть видеоролик Знакомство с системами координат и картографическими проекциями, чтобы узнать больше обо всех этих терминах и концепциях. Вы также можете прочитать эти другие статьи, которые я написал о системах координат:
- Географические и проекционные системы координат
- Проекция на лету и географические преобразования
- Определить проекцию или проект?
- Предупреждение о трансформации: что это значит и что мне делать?
Большое спасибо Бояну Шавричу и Мелите Кеннеди за их помощь и поддержку в написании этой и других недавних статей!
Бесплатная пробная версия ArcGIS Pro
Об авторе
Хизер Смит
Хизер — картограф и художник, который сочетает обе практики, чтобы выразить и понять пейзажи. Она пишет и редактирует уроки для веб-сайта Learn ArcGIS. Посмотреть больше ее работ можно на сайте www.heathergabrielsmith.ca
Она пишет и редактирует уроки для веб-сайта Learn ArcGIS. Посмотреть больше ее работ можно на сайте www.heathergabrielsmith.ca
.
3.2: Системы координат — LibreTexts по физике
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 24432
- Питер Дурмашкин
- Массачусетский технологический институт через MIT OpenCourseWare
0
Физика занимается изучением явлений, которые мы наблюдаем в мире. Чтобы связать явления с математикой, мы начнем с введения понятия системы координат. Система координат состоит из четырех основных элементов:
- Выбор происхождения
- Выбор осей
- Выбор положительного направления для каждой оси
- Выбор единичных векторов в каждой точке пространства
Обычно используются три системы координат: декартова, цилиндрическая и сферическая.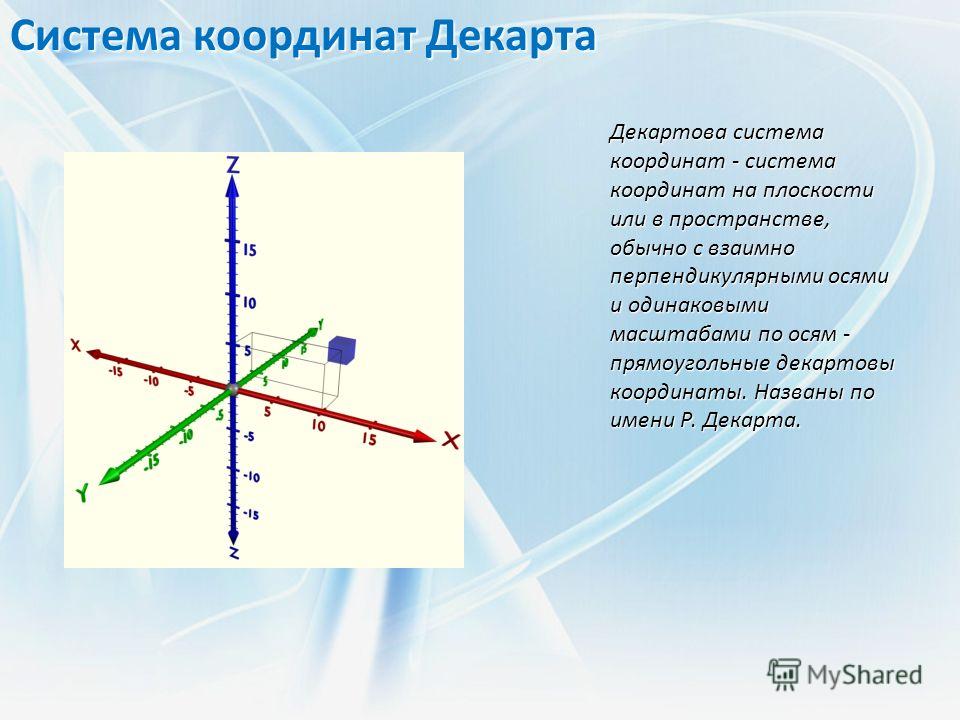 В этой главе мы опишем декартову систему координат и цилиндрическую систему координат.
В этой главе мы опишем декартову систему координат и цилиндрическую систему координат.
Декартова система координат
Декартовы координаты состоят из набора взаимно перпендикулярных осей, которые пересекаются в общей точке, начале координат \(O\). Мы живем в трехмерном пространственном мире; по этой причине наиболее распространенная система, которую мы будем использовать, имеет три оси.
Выбор пункта отправления
Выберите пункт отправления O в любой наиболее удобной точке.
Выбор осей
Простейший набор осей известен как декартовы оси, \(x\)-ось, \(y\)-ось и \(z\)-ось, которые находятся под прямым углом по отношению друг к другу. Тогда каждой точке \(P\) в пространстве можно поставить в соответствие тройку значений \(\left(x_{P}, y_{P}, z_{P}\right)\). Диапазоны этих значений: \(-\infty Наш третий выбор — назначение положительного направления для каждой оси координат. Теперь свяжем каждой точке \(P\) в пространстве набор из трех единичных векторов \(\left(\hat{\mathbf{i}}_{P}, \hat{\mathbf{j}} _{P}, \hat{\mathbf{k}}_{P}\right)\). Единичный вектор имеет величину один: \(\left|\hat{\mathbf{i}}_{P}\right|=1,\left|\hat{\mathbf{j}}_{P}\right| = 1, \ text { и } \ left | \ hat {\ mathbf {k}} _ {P} \ right | = 1 \). Мы назначаем направление \(\hat{\mathbf{i}}_{P}\) точке в направлении возрастания \(x\)-координаты в точке \(P\). Определим направления для \(\hat{\mathbf{j}}_{P}\) и \(\hat{\mathbf{k}}_{P}\) \(P\) в направлении по возрастанию \(y\)-координаты и \(z\)-координаты соответственно (рис. , потому что векторы равны, если они имеют одинаковое направление и величину независимо от того, где они расположены в пространстве. Рис. 3.10 Выбор единичных векторов в точках P и S . (CC BY-NC; Ümit Kaya) Декартова система координат – это единственная система координат, в которой уравнение (3.2.1) выполняется для всех пар точек. Поэтому мы опускаем ссылку на точку P и используем \(\left(\hat{\mathbf{i}}_{P}, \hat{\mathbf{j}}_{P}, \hat{\mathbf{ k}}_{P}\right)\) для представления единичных векторов в декартовой системе координат (рис. Рис. 3.11. Единичные векторы в декартовой системе координат. (CC BY-NC; Юмит Кая) Многие физические объекты демонстрируют тот или иной тип симметрии. Например, если вы вращаете однородный цилиндр вокруг продольной оси (оси симметрии), цилиндр остается неизменным. Операция вращения цилиндра называется операцией симметрии, а объект, подвергаемый операции, цилиндр, точно такой же, как и до выполнения операции. Это свойство симметрии цилиндров предполагает систему координат, называемую цилиндрической системой координат, которая делает свойство симметрии относительно вращения прозрачным. Сначала выберите начало координат \(O\) и ось, проходящую через \(O\), которую мы называем осью \(z\). Цилиндрические координаты для точки \(P\) представляют собой три числа \((r,θ,z)\) (рис. 3.12). Число \(z\) представляет известную координату точки \(P\) вдоль оси \(z\). Неотрицательное число r представляет собой расстояние от оси \(z\) до точки \(P\). Рисунок 3.12 Цилиндрические координаты. (CC BY-NC; Ümit Kaya) Координаты \((r,θ)\) называются полярными координатами . Преобразования координат между \((r, θ)\) и декартовыми координатами \((x, y)\) задаются как \[x=r \cos \theta, \nonumber \] \[y = г \ грех \ тета. \nonumber \] Наоборот, если нам даны декартовы координаты \((x, y)\), координаты \((r,θ)\) могут быть определены из преобразований координат\[r=+\left (x^{2}+y^{2}\right)^{1 / 2} \nonumber \] 9{-1}(y / x) \nonumber \] Выбираем набор единичных векторов \(\left(\hat{\mathbf{r}}_{P}, \hat{\mathbf{θ}} _{P}, \hat{\mathbf{k}}_{P}\right)\) в точке \(P\) следующим образом. Рисунок 3.13: (a) Единичные векторы в двух разных точках в цилиндрических координатах. (b) Единичные векторы в полярных координатах и декартовых координатах. (CC BY-NC; Ümit Kaya) Единичные векторы \((\hat{\mathbf{r}}, \hat{\boldsymbol{\theta}})\) в точке \(P\) также связаны с декартовыми единичными векторами \((\hat{\mathbf{i}}, \hat{\mathbf{j}})\) преобразованиями \[\hat{\mathbf{r}}=\ cos \ theta \, \ hat {\ mathbf {i}} + \ sin \ theta \, \ hat {\ mathbf {j}} \ nonumber \] \[\hat{\mathbf{θ}}=-\sin\theta\, \hat{\mathbf{i}}+\cos\theta\, \hat{\mathbf{j}} \nonumber \] Аналогично, обратные преобразования задаются как {θ}} \nonumber \] \[\hat{\mathbf{j}}=\sin\theta\, \hat{\mathbf{r}}+\cos\theta\, \hat{\mathbf{ θ}} \nonumber \] Цилиндрическая система координат также является полезным выбором для описания движения объекта, движущегося по окружности вокруг центральной точки. Рассмотрим вертикальную ось, проходящую перпендикулярно плоскости движения, проходящей через эту центральную точку. Выбор положительного направления
 Обозначим этот выбор символом \(+\) вдоль положительной оси. В физических задачах мы вольны выбирать оси и положительные направления любым способом, который, по нашему мнению, лучше всего подходит для данной задачи. Проблемы, которые очень сложны при использовании 6 обычных вариантов, могут оказаться намного проще решить, если сделать вдумчивый выбор осей.
Обозначим этот выбор символом \(+\) вдоль положительной оси. В физических задачах мы вольны выбирать оси и положительные направления любым способом, который, по нашему мнению, лучше всего подходит для данной задачи. Проблемы, которые очень сложны при использовании 6 обычных вариантов, могут оказаться намного проще решить, если сделать вдумчивый выбор осей. Выбор единичных векторов
 3.10). Если мы выберем другую точку \(S\) и определим аналогичный набор единичных векторов \(\left(\hat{\mathbf{i}}_{S}, \hat{\mathbf{j}}_{ S}, \hat{\mathbf{k}}_{S}\right)\), единичные векторы в точках \(S\) и P удовлетворяют равенствам \[\hat{\mathbf{i}}_{S } = \ шляпа {\ mathbf {i}} _ {P}, \ шляпа {\ mathbf {j}} _ {S} = \ шляпа {\ mathbf {j}} _ {P}, \ text {и} \ шляпа {\ mathbf {k}} _ {S} = \ шляпа {\ mathbf {k}} _ {P}, \ nonumber \]
3.10). Если мы выберем другую точку \(S\) и определим аналогичный набор единичных векторов \(\left(\hat{\mathbf{i}}_{S}, \hat{\mathbf{j}}_{ S}, \hat{\mathbf{k}}_{S}\right)\), единичные векторы в точках \(S\) и P удовлетворяют равенствам \[\hat{\mathbf{i}}_{S } = \ шляпа {\ mathbf {i}} _ {P}, \ шляпа {\ mathbf {j}} _ {S} = \ шляпа {\ mathbf {j}} _ {P}, \ text {и} \ шляпа {\ mathbf {k}} _ {S} = \ шляпа {\ mathbf {k}} _ {P}, \ nonumber \]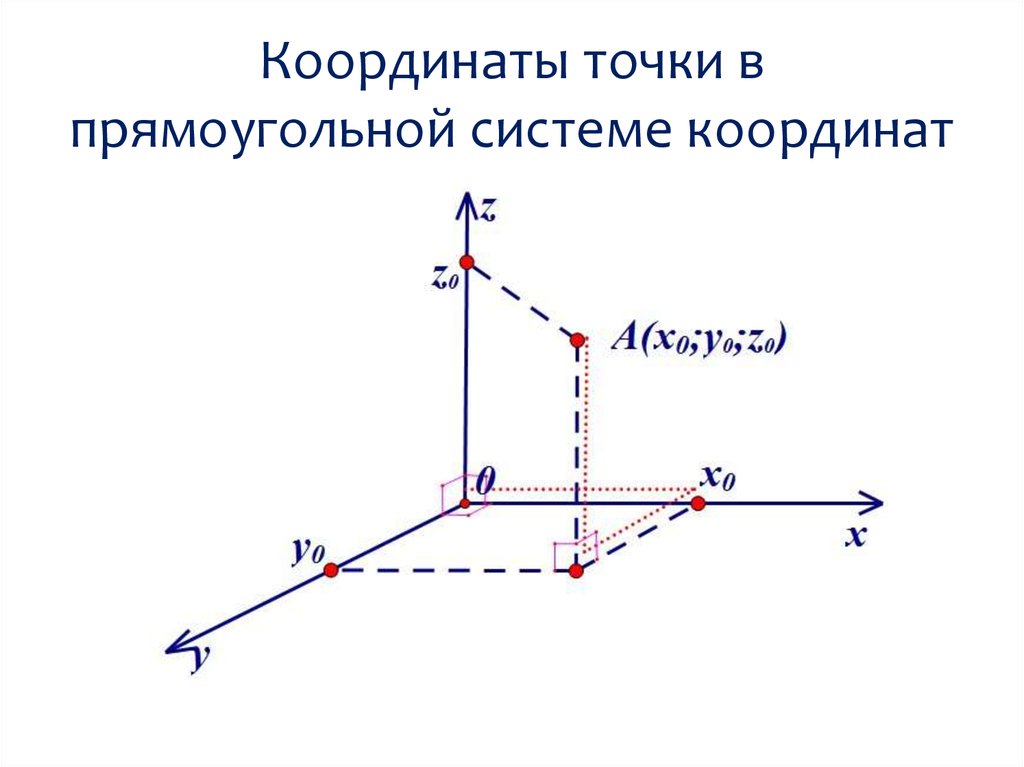 3.11).
3.11). Цилиндрическая система координат
 Точки пространства, соответствующие постоянному положительному значению \(г\), лежат на круговом цилиндре. Геометрическое место точек, соответствующих \(r = 0\), является осью \(z\). В плоскости \(z = 0\) определите опорный луч, проходящий через \(O\), который мы будем называть положительной осью \(x\). Проведите через точку \(P\) прямую, параллельную оси \(z\). Пусть \(D\) обозначает точку пересечения этой линии \(PD\) с плоскостью \(z = 0\). Проведите луч \(OD\) из начала координат в точку \(D\). Пусть \(θ\) обозначает направленный угол от опорного луча к лучу \(OD\). Угол \(θ\) положителен при измерении против часовой стрелки и отрицателен при измерении по часовой стрелке.
Точки пространства, соответствующие постоянному положительному значению \(г\), лежат на круговом цилиндре. Геометрическое место точек, соответствующих \(r = 0\), является осью \(z\). В плоскости \(z = 0\) определите опорный луч, проходящий через \(O\), который мы будем называть положительной осью \(x\). Проведите через точку \(P\) прямую, параллельную оси \(z\). Пусть \(D\) обозначает точку пересечения этой линии \(PD\) с плоскостью \(z = 0\). Проведите луч \(OD\) из начала координат в точку \(D\). Пусть \(θ\) обозначает направленный угол от опорного луча к лучу \(OD\). Угол \(θ\) положителен при измерении против часовой стрелки и отрицателен при измерении по часовой стрелке.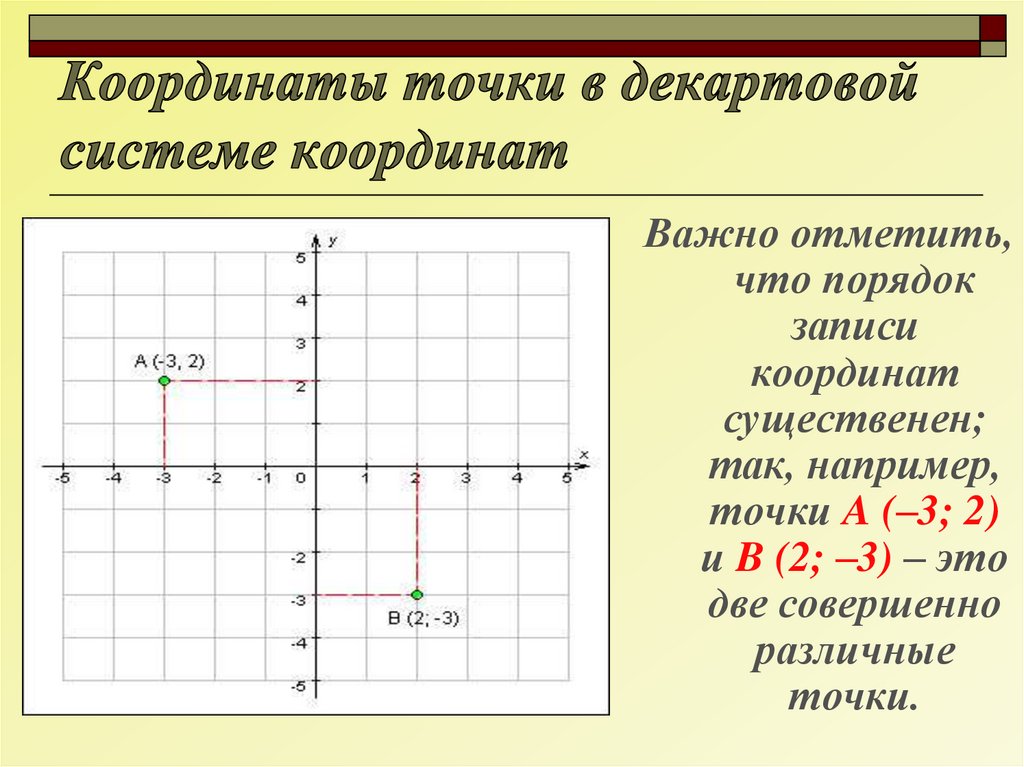 Мы выбираем \( \hat{\mathbf{k}}_{P} \) так, чтобы он указывал в направлении увеличения \(z\). Мы выбираем \(\hat{\mathbf{r}}_{P}\) так, чтобы он указывал в направлении увеличения \(r\), направленном радиально от оси \(z\). Мы выбираем \(\hat{\mathbf{θ}}_{P}\) так, чтобы он указывал в направлении увеличения \(θ\). Этот единичный вектор направлен против часовой стрелки и касается окружности (рис. 3.13а). Одно важное различие между цилиндрическими координатами и декартовыми координатами связано с выбором единичных векторов. Предположим, мы рассматриваем другую точку \(S\) на плоскости. Единичные векторы \(\left(\hat{\mathbf{r}}_{\mathrm{s}}, \hat{\boldsymbol{\theta}}_{\mathrm{s}}, \hat{\mathbf {k}}_{\mathrm{s}}\right)\) в точке \(S\) также показаны на рис. 3.13. Обратите внимание, что \(\hat{\mathbf{r}}_{P} \neq \hat{\mathbf{r}}_{S} \text {и} \hat{\boldsymbol{\theta}}_{p } \neq \hat{\boldsymbol{\theta}}_{S}\), потому что их направление отличается. Мы опускаем нижние индексы, обозначающие точки, в которых определены единичные векторы, и просто ссылаемся на набор единичных векторов в точке как \((\hat{\mathbf{r}}, \hat{\boldsymbol{\theta }}, \hat{\mathbf{k}})\), при том понимании, что направления набора \((\hat{\mathbf{r}}, \hat{\boldsymbol{\theta}})\ ) зависят от положения рассматриваемой точки.
Мы выбираем \( \hat{\mathbf{k}}_{P} \) так, чтобы он указывал в направлении увеличения \(z\). Мы выбираем \(\hat{\mathbf{r}}_{P}\) так, чтобы он указывал в направлении увеличения \(r\), направленном радиально от оси \(z\). Мы выбираем \(\hat{\mathbf{θ}}_{P}\) так, чтобы он указывал в направлении увеличения \(θ\). Этот единичный вектор направлен против часовой стрелки и касается окружности (рис. 3.13а). Одно важное различие между цилиндрическими координатами и декартовыми координатами связано с выбором единичных векторов. Предположим, мы рассматриваем другую точку \(S\) на плоскости. Единичные векторы \(\left(\hat{\mathbf{r}}_{\mathrm{s}}, \hat{\boldsymbol{\theta}}_{\mathrm{s}}, \hat{\mathbf {k}}_{\mathrm{s}}\right)\) в точке \(S\) также показаны на рис. 3.13. Обратите внимание, что \(\hat{\mathbf{r}}_{P} \neq \hat{\mathbf{r}}_{S} \text {и} \hat{\boldsymbol{\theta}}_{p } \neq \hat{\boldsymbol{\theta}}_{S}\), потому что их направление отличается. Мы опускаем нижние индексы, обозначающие точки, в которых определены единичные векторы, и просто ссылаемся на набор единичных векторов в точке как \((\hat{\mathbf{r}}, \hat{\boldsymbol{\theta }}, \hat{\mathbf{k}})\), при том понимании, что направления набора \((\hat{\mathbf{r}}, \hat{\boldsymbol{\theta}})\ ) зависят от положения рассматриваемой точки.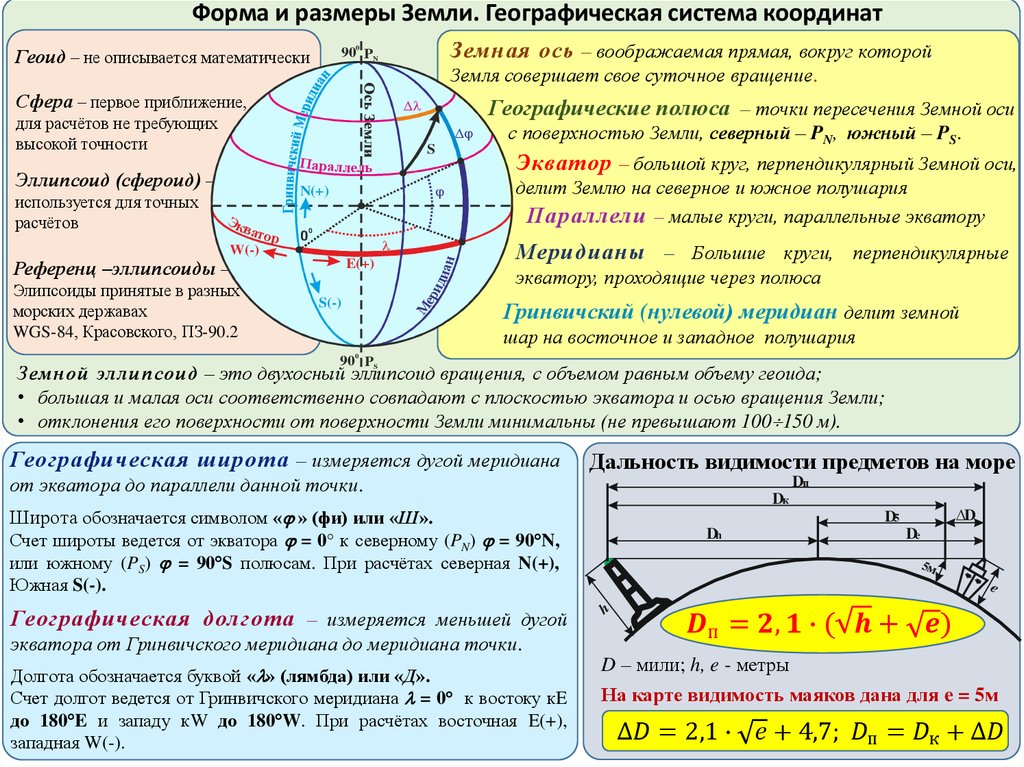

 также
также
Всего комментариев: 0