Что такое опорные точки в чпу: Опорные точки и геометрические элементы
Содержание
Опорные точки и геометрические элементы
Опорная
точка
— точка расчетной траектории, в которой
происходит изменение либо закона,
описывающего траекторию, либо условий
протекания технологического процесса.
Опорная
геометрическая точка
— точка расчетной траектории, в которой
происходит изменение закона, описывающего
траекторию.
Опорная
технологическая точка
— точка расчетной траектории, в которой
происходит изменение условий протекания
технологического процесса.
Геометрический
элемент
— непрерывный участок расчетной
траектории или контура детали, задаваемый
одним и тем же законом в одной и той же
системе координат.
Расчетная
траектория
— теоретическая аппроксимированная
относительная траектория центра
инструмента.
Процессоры
и постпроцессоры
Процессор
—
программа первичной переработки
информации в САП, формирующая данные
по обработке детали безотносительно к
типу станка.
Пост
процессор
— согласующая программа САП, учитывающая
особенности данного станка и формирующая
кадр.
Написание
и хранение информации
Рукопись
программы
– информация, записанная в виде, удобном
для составления языковой или управляющей
программы.
Файл
– совокупность данных, объединенных
по некоторому общему смысловому признаку
или несколькими признаками. Способ
хранения информации в виде файла (данных)
широко применяется в запоминающих
устройствах ЭВМ. При этом начало и конец
файла отмечают специальными метками,
что позволяет легко найти соответствующую
информацию (например, на магнитной
ленте)
Дисплей
— устройство визуального отображения
алфавитно-цифровой и графической
информации. Наиболее распространены
дисплеи телевизионного типа.
Интерфейс
—
совокупность аппаратных и программных
средств, обеспечивающих совместимость
(взаимодействие) различных функциональных
блоков (устройств), образующих
измерительную, вычислительную или
управляющую систему, в соответствии с
требуемыми условиями, например видом
кода, моментом выдачи (приема) информационных
и управляющих сигналов, формой
представления информации (аналоговая
или цифровая).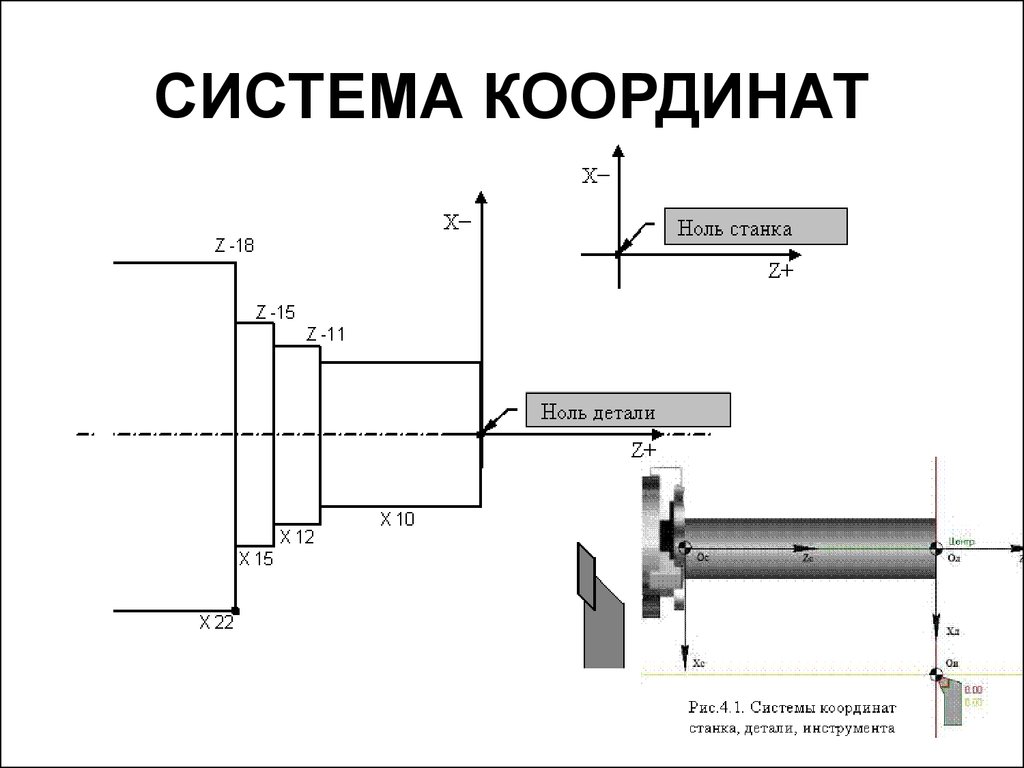
Ось
координат станка с ЧПУ—
направление, совпадающее с перемещением
рабочего органа станка по направляющей
опоре в соответствии с программой
управления станком, связанное с одной
единицей привода.
Управляемая
координата
— ось системы координат, относительное
перемещение вдоль которой центра
инструмента осуществляется с помощью
одного исполнительного органа системы
управления.
Шаг
программирования
— разность между двумя ближайшими
программируемыми числовыми величинами.
Чувствительность
системы управления
— минимальное рассогласование, на
которое может реагировать система.
Точность
позиционирования
— величина поля рассеивания отклонений
положений центра инструмента от заданных
при отработке геометрического перехода
без резания, рассчитанная для всего
диапазона задаваемых размеров.
Управляемая
координата и точность позиционирования
Центр
инструмента
— неподвижная относительно державки
точка инструмента, по которой ведется
расчет траектории.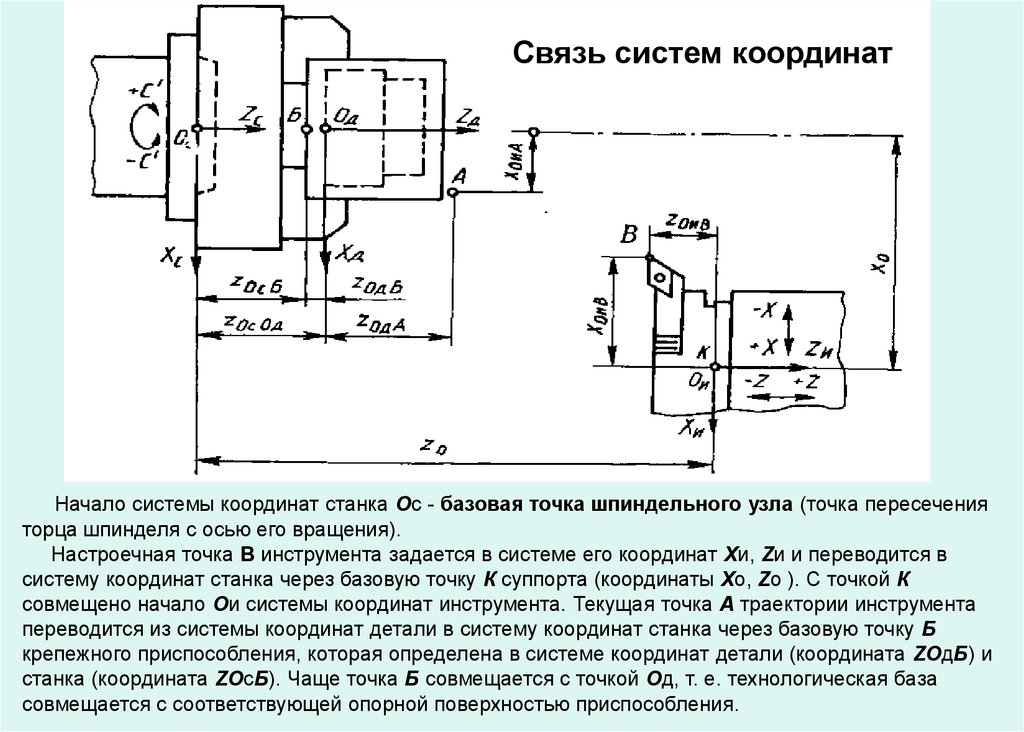
Эвидистанта
— линия, равноотстоящая от линии контура
детали (заготовки).
Интерполятор
системы ЧПУ станком
— вычислительный блок системы ЧПУ,
задающий последовательность управляющих
воздействий для перемещения рабочих
органов станка по осям координат в
соответствии с функциональной связью
между координатами опорных точек,
заданных программой управления станком.
Основные
нулевые точки станков с ЧПУ
Контурная
скорость
— результирующая скорость подачи
рабочего органа станка, вектор которой
равен геометрической сумме векторов
скоростей перемещения этого органа
вдоль осей координат станка.
Дискретность
задания перемещения
— минимальное перемещение или угол
поворота рабочего органа станка, которые
могут быть заданы в УП.
Дискретность
отработки перемещения
— минимальное перемещение или угол
поворота рабочего органа станка,
контролируемые в процессе управления
Дискретность и интерполяция в современных системах ЧПУ
Для работы ЧПУ необходим интерполятор – вычислительное устройство, которое передаёт информацию от PC, преобразуя в координаты.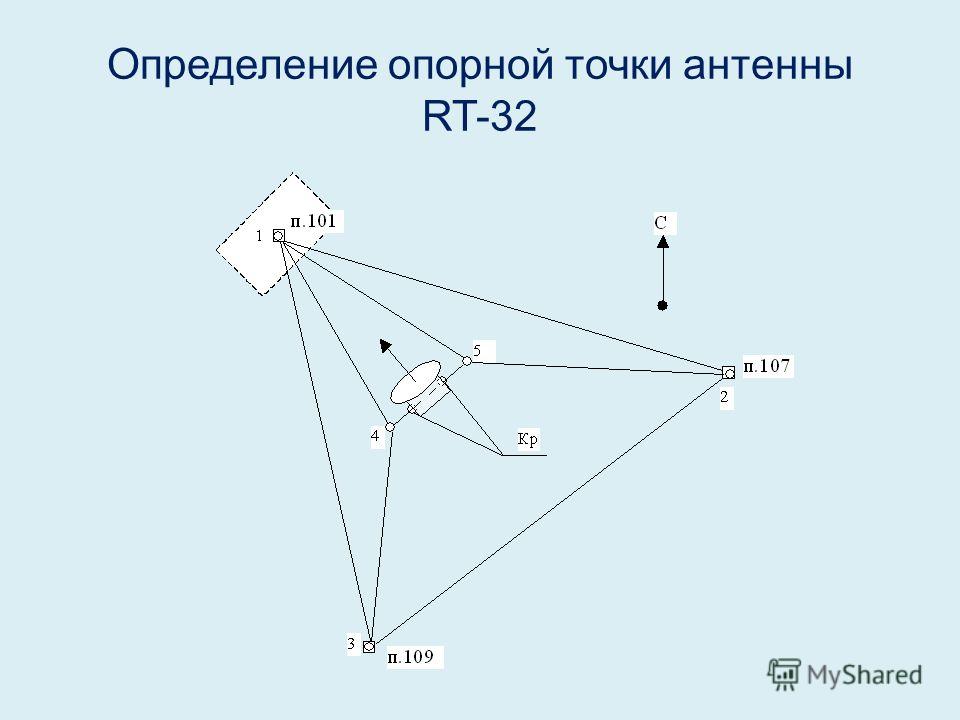 Есть два вида интерполяторов: линейные и линейно-круговые. Работают оба по принципу подачи импульса (интерполяции). Шаг, осуществляемый от одного импульса, называется дискретностью. Интерполяторы имеют важнейшее качество поддерживать заданную подачу между опорными точками неизменной.
Есть два вида интерполяторов: линейные и линейно-круговые. Работают оба по принципу подачи импульса (интерполяции). Шаг, осуществляемый от одного импульса, называется дискретностью. Интерполяторы имеют важнейшее качество поддерживать заданную подачу между опорными точками неизменной.
Один из главных узлов контурных УЧПУ – это интерполятор (специальное вычислительное устройство). Интерполятор преобразует программа заданную от PC информацию непосредственно в управляющие действия на двигатели приводов подач для обеспечения требуемой траектории и скорости движения инструмента вдоль заданного контура.
Траектория перемещения инструмента относительно детали/заготовки в программе задается значениями координат отдельно взятых точек А, В, С…, так называемыми – опорными точками. Характер движения инструмента между этими опорными точками определяется естественно видом интерполяции, которую непосредственно и выполняет – интерполятор.
Сегодня в современных системах ЧПУ в основном применяются интерполяторы двух типов:
- линейные (обеспечивают перемещение инструмента между соседствующими опорными точками по прямым линиям, которые расположены под любыми углами):
- линейно-круговые (реализуют характер управления, то есть инструмент между соседствующими опорными точками способен перемещаться и по прямым линиям и по дугам окружностей).
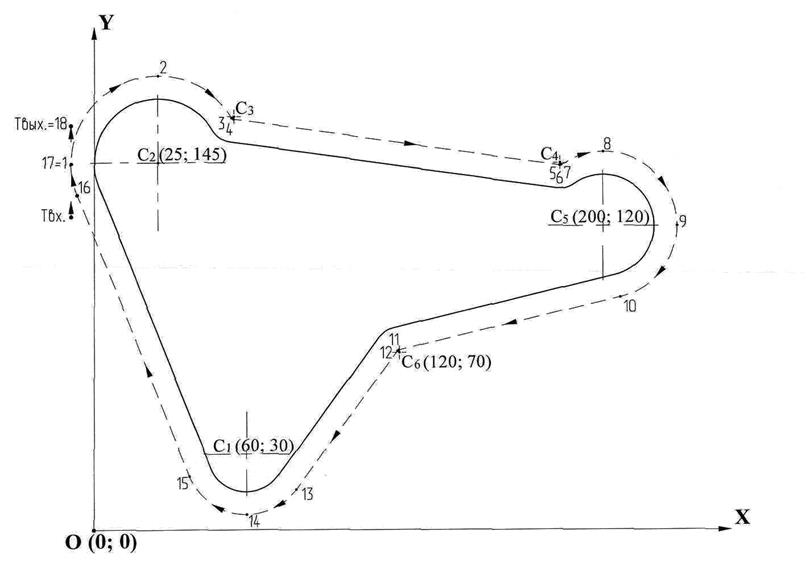
Для осуществления кругового движения в программе помимо координат опорных точек обязательно должны быть заданы еще и координаты центров дуг окружностей. Как правило, в большинстве современных контурных системах ЧПУ, рабочие органы для перемещения получают команды дискретно, то есть в виде единичных кратковременных управляющих импульсов (управляющих воздействий).
Использование интерполятора в новейших системах ЧПУ
Интерполятор в свою очередь обеспечивает распределение поступающих импульсов между приводами подач, чтобы инструмент перемещался максимально близко к дуге окружности (в случае круговой интерполяции) или к заданной прямой (в случае линейной интерполяции) с обусловленными шагами движений. Меньше всего контролируется шаг в процессе управления в перемещении рабочего органа, который осуществляется от одного управляющего импульса и называется дискретностью отработки перемещений («разрешающая способность СЧПУ»). Между опорными точками схема движения инструмента выглядит так: А, В, С, Д, Е при линейной интерполяции (а) и опорными точками А, В, С при круговой интерполяции (б) при токарной обработке.
На один управляющий импульс, который выдается интерполятором, дискретность отработки перемещений формулируется в миллиметрах. В большинстве своем современные системы ЧПУ имеют дискретность отработки передвижений, равную 0,01 мм/имп. В свою очередь новые СЧПУ, осваиваемые сегодня, рассчитаны уже на дискретность в 0,001 мм/имп. Конструкция УЧПУ, двигатели подач и датчики обратной связи, обеспечивают четкое выполнение станком необходимых значений дискретности, сюда же относится передаточное отношения механизмов подач станков.
Аппроксимация контура
Во время разработки программ для станков непосредственно с линейными интерполяторами криволинейный контур, который заданный на чертеже, замещают ломаной линией. Данная замена называется «аппроксимацией контура». Во время аппроксимации, точки ломаной линии должны отклоняться от заданного контура – как можно меньше. Однако уменьшение таких отклонений приводит к неизбежному увеличению числа опорных точек, к увеличению числа кадров непосредственно в самой программе и соответственно к увеличению объема вычислений определяющих их координат.
На практике же число опорных точек принимается минимально допустимым, чтобы максимальное их отклонение от заданного контура ни в коем случае не превышало допуска δ непосредственно на аппроксимацию контура. Этот допуск принимается равным: δ= (0,1—0,3)Δ, где Δ, то есть – на размеры заданного контура чертежный допуск.
Поскольку в кадре программы записывается лишь только координаты конечных точек дуги исключительно каждого радиуса и соответственно координаты центров этих дуг (к примеру, такие точки как, В и С и O1 и O2), то программирование для станков, имеющих линейно-круговые интерполяторы – считается более простым.
Круговая интерполяция
Однако круговая интерполяция может быть использована, причем достаточно, просто, только в том случае, когда обрабатываемый контур задан участками исключительно дуг окружностей известных ей радиусов. Но если участок дугой окружности не является, то приходится использовать, либо линейную интерполяцию с аппроксимацией контура ломаной линией, либо выполнять аппроксимацию криволинейного контура (к примеру, параболы) участками дуг окружностей.
Наибольшие преимущества при токарных обработках дает круговая интерполяция, потому как контуры осевых сечений вращения тел в большинстве своем очерчиваются дугами окружностей. Если сравнивать с токарными обработками, обычно при которых программируется траектория движения вершины резца, как правило, при фрезеровании, программируется только траектория движения центра фрезы. Траектория движения центра фрезы непосредственно с радиусом Rф при создании контура ABC, который состоит из двух дуг окружностей с радиусом R1 и R2 (А1, В1, В1′, С1 — то есть, опорные точки траектории движения самой фрезы).
Чтобы обеспечить правильное формирование обрабатываемой поверхности, данная траектория по отношению исключительно к заданному контуру основывается в виде эквидистантной кривой. Эквидистантной называется кривая, у которой все точки удалены на одно расстояние от заданного контура. При фрезеровании таким расстоянием основным, конечно же, является радиус фрезы. Размеры и форма эквидистантной кривой существенно отличаются от контура детали, именно поэтому программирование для фрезерных станков зачастую связано с достаточно резким увеличением объема вычислений.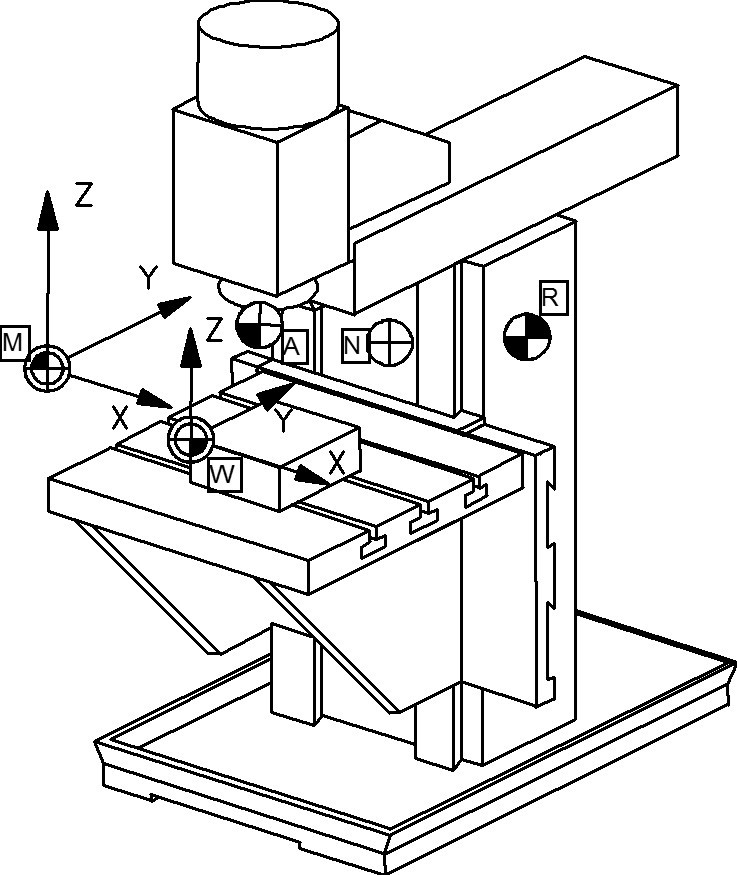
Преимущества интерполяции
Преимуществ от использования круговой интерполяции во время фрезерования меньше, чем во время токарной обработки, потому что многие детали, которые изготавливаются на фрезерных станках, обязательно очерчиваются контурами, которые в свою очередь составлены из более сложных кривых, нежели дуги окружностей. Кроме этого, современные линейно-круговые интерполяторы четко обеспечивают относительное движение инструмента исключительно по окружностям, расположенным следующим образом: в плоскости стола, а также в плоскости перпендикулярно направлению продольной подачи стола, а также в плоскости перпендикулярно направлению поперечной подачи стола.
Именно это действие не позволяет рационально аппроксимировать достаточно сложные фасонные поверхности дугами окружностей. Посему на фрезерных станках с (числовым программным управлением) наиболее широко применяется более простая и в тоже время универсальная линейная интерполяция, соответственно при ее воздействии инструмент перемещается по прямой линии из точки М, например, в точку N. При этом траектория перемещения концевой сферической фрезы непосредственно в опорную точку N из опорной точки М при линейной интерполяции осуществляется с одновременным управлением исключительно по трем координатам.
При этом траектория перемещения концевой сферической фрезы непосредственно в опорную точку N из опорной точки М при линейной интерполяции осуществляется с одновременным управлением исключительно по трем координатам.
Технологические качества интерполяции
Абсолютно все интерполяторы обладают важнейшим технологическим качеством: при линейной интерполяции они отлично поддерживают заданную системой контурную скорость движения инструмента (т. е. подачу) в промежутке между соседствующими опорными точками неизменной (т. е. стабильной). Это обеспечивается благодаря постоянству частоты выдачи управляющих импульсов, формирующиеся интерполятором в соответствии с необходимой информацией о величине подачи, которая записана в кадре управляющей программы.
Если возникает необходимость, то в автоматическом режиме эта подача может быть изменена на другую абсолютно в любой опорной точке на наиболее рациональную. Если подачу нужно изменить в промежутке между главными опорными точками, то назначают промежуточные опорные точки. Также необходимо учесть, что при круговой интерполяции заданное постоянство частоты управляющих импульсов (их выдачи) приводит подачи вдоль дуги окружности к некоторой неравномерности.
Также необходимо учесть, что при круговой интерполяции заданное постоянство частоты управляющих импульсов (их выдачи) приводит подачи вдоль дуги окружности к некоторой неравномерности.
Работа с текстом — Руководство по ЧПУ
Редактирование интервала между текстом и кривой
Функция «Редактирование интервала между текстом и кривой» дает вам специальный курсор, который позволяет легко регулировать кривизну текстового поля и интервал между символами (кернинг) . Выберите текстовое поле, а затем выберите функцию на левой панели.
Кернинг
Чтобы настроить расстояние между отдельными символами, просто щелкните между двумя символами, которые вы хотите настроить. Щелчок по умолчанию сближает их, а удерживание Shift при щелчке разделяет их. Обратите внимание, что если вы впоследствии отредактируете текст и измените эти символы, любые настройки кернинга будут потеряны.
Кривизна
С помощью этого инструмента также можно придать тексту базовую кривую (для более сложных настроек траектории текста используйте функцию «Текст на кривой», описанную ниже).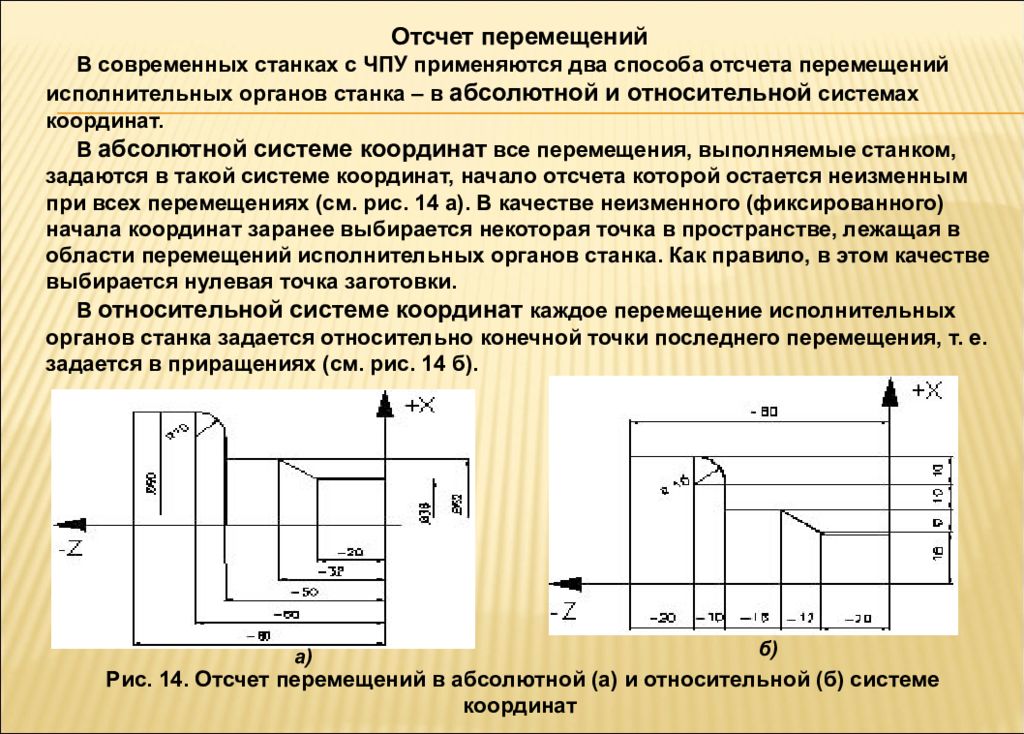 Выберите текст и возьмите любой из зеленых прямоугольников, чтобы изогнуть его вверх или вниз. Как только текст искривится, в верхних углах появятся красные прямоугольники, а в нижних — синие. Перетаскивание красных полей позволит вам вращать текст вокруг кривой, а синие будут увеличивать или уменьшать расстояние текстового поля от центральной точки. Изменение текста после редактирования кривой обычно не приводит к потере изменений кривой, однако «круг» может быть расширен, если добавлено большое количество текста.
Выберите текст и возьмите любой из зеленых прямоугольников, чтобы изогнуть его вверх или вниз. Как только текст искривится, в верхних углах появятся красные прямоугольники, а в нижних — синие. Перетаскивание красных полей позволит вам вращать текст вокруг кривой, а синие будут увеличивать или уменьшать расстояние текстового поля от центральной точки. Изменение текста после редактирования кривой обычно не приводит к потере изменений кривой, однако «круг» может быть расширен, если добавлено большое количество текста.
Преобразовать в кривые
Для большинства типов векторных объектов объект просто сохраняется в виде списка вершин (узлов), и когда программа отображает их, она считывает список и строит объект. Текст отличается тем, что он хранится в виде массива символов с данными о том, как он размечен, включая используемый шрифт. При отображении текстового поля программное обеспечение должно искать шрифт в операционной системе для построения текста. Поэтому, если файл VCarve создается на компьютере с определенным шрифтом, а затем перемещается на компьютер без этого шрифта, он не сможет правильно его отобразить.
Поэтому, если файл VCarve создается на компьютере с определенным шрифтом, а затем перемещается на компьютер без этого шрифта, он не сможет правильно его отобразить.
Если специальный шрифт (например, загруженный из Интернета) используется при создании текста дома, а затем вносится в компьютер PPLD, подключенный к ЧПУ, шрифт будет недоступен. Сотрудники PPLD ни при каких обстоятельствах не будут устанавливать пользовательские шрифты. Чтобы получить текст с сохраненным шрифтом, нужно преобразовать текстовое поле в стандартный векторный объект. Это можно сделать, просто выделив текстовое поле и нажав Convert to Curves. Теперь текст будет храниться в виде набора узлов, благодаря чему он будет выглядеть одинаково на любом компьютере.
Это односторонняя операция — после преобразования в кривые ее уже нельзя будет снова превратить в текстовое поле. Это означает, что шрифт, символы, интервалы и т. д. нельзя легко изменить.
Лучшее решение — после того, как проект будет полностью завершен с точки зрения дизайна — сделать вторую копию файла, а затем преобразовать весь текст в этом файле в кривые. Таким образом, если вам нужно внести какие-либо изменения, вы можете просто вернуться к исходному файлу без необходимости перестраивать текстовое поле.
Таким образом, если вам нужно внести какие-либо изменения, вы можете просто вернуться к исходному файлу без необходимости перестраивать текстовое поле.
Почти каждая программа векторного дизайна, которая может работать с текстом, имеет функцию преобразования текста в кривые, хотя она может называться по-другому. В Inkscape это можно сделать, выбрав «Объект в путь» в меню «Путь». В Illustrator это делается путем создания контура текста, а затем перемещения или скрытия текстового поля.
Текст на кривой
Хотя функция «Редактировать текстовое пространство и кривая» может легко придать тексту форму кривой, если вам нужны дополнительные параметры или вы хотите, чтобы текст отображался по другой форме, функция «Текст на кривой» будет полезна. . Несмотря на название, он может помещать текст в любой вектор, включая замкнутые многоугольники и (поли)линии.
Просто создайте и текстовое поле, и векторный контур, выберите оба, а затем щелкните значок «Текст на кривой» на левой панели.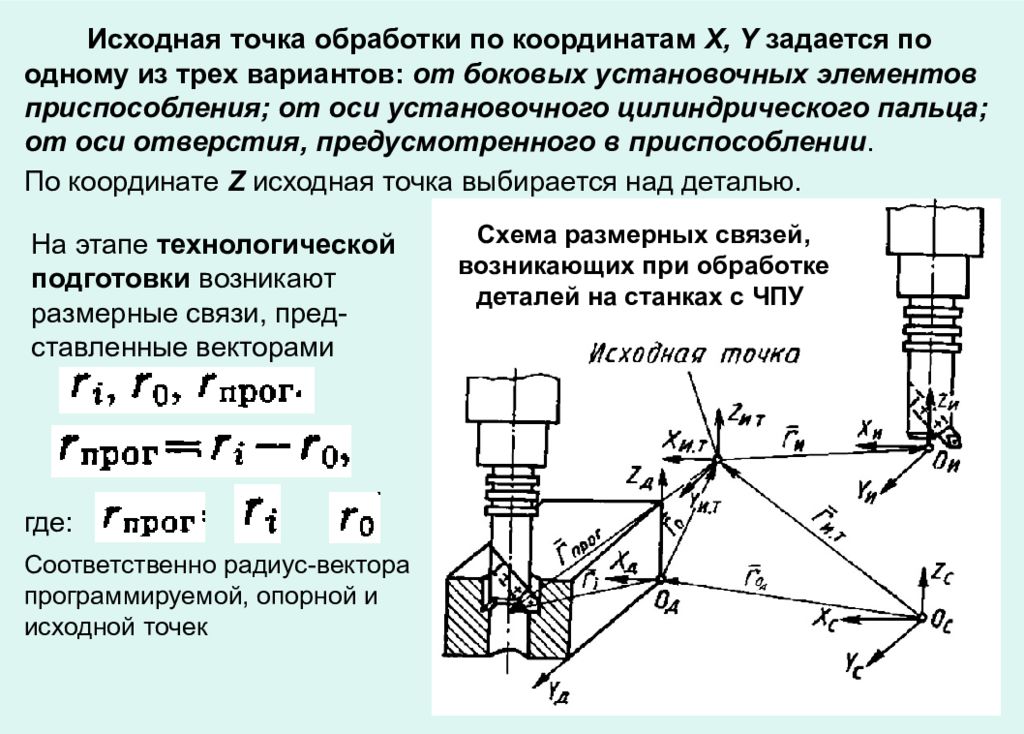 Он автоматически переместит текст на кривую с настройками по умолчанию. Оттуда вы можете манипулировать кривой с помощью панели параметров или мыши.
Он автоматически переместит текст на кривую с настройками по умолчанию. Оттуда вы можете манипулировать кривой с помощью панели параметров или мыши.
Параметры
- Размер текста: текст может быть либо сохранен в исходном размере, либо автоматически скорректирован в соответствии с контуром.
- Интервал текста: регулирует интервал между символами.
- Положение текста: перемещает текст вверх/вне, вниз/внутрь или через середину контура. Если текст перевернут, просто установите флажок «Текст на другой стороне», чтобы перевернуть его. Расстояние смещения можно использовать, чтобы отодвинуть текст от контура.
- Выравнивание текста: перемещает текст влево, вправо или по центру, если он короче пути. Кроме того, вы можете настроить автоматическое вращение символов в соответствии с изгибом траектории или их вертикальное положение, в то время как текст в целом перемещается по траектории.
Путь можно изменить с помощью мыши. В дополнение к стандартным точкам привязки для перемещения, изменения размера и поворота текста можно перетаскивать синюю привязку в центре для перемещения текста по пути.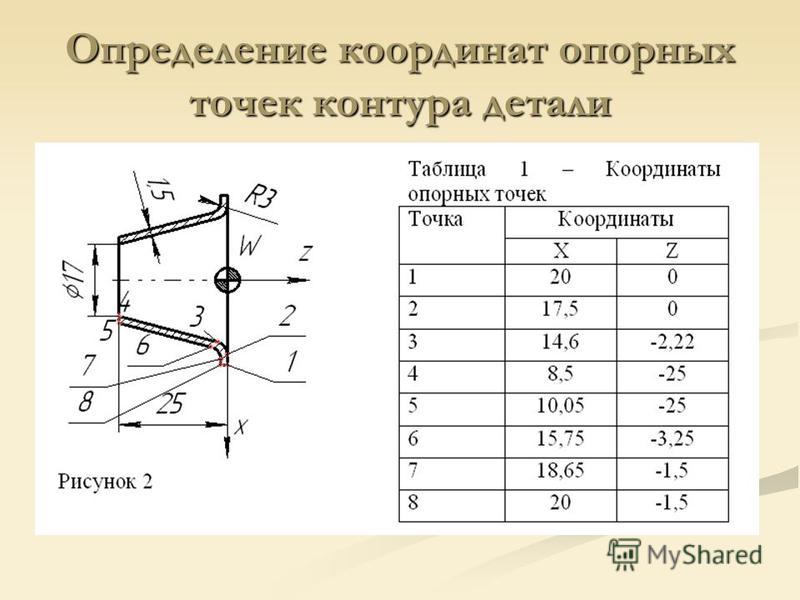
После этого путь можно безопасно переместить или удалить, не затрагивая текст. Даже если исходный путь будет удален, вы сможете изменить текст, выбрав его и снова щелкнув значок на левой панели. Данные пути теперь являются частью текстового поля и останутся, даже если текст будет изменен. Как правило, путь будет автоматически обновлен в соответствии с новым размером текстового поля, но впоследствии может потребоваться его точная настройка. Чтобы полностью удалить изменения, щелкните текст правой кнопкой мыши и выберите «Удалить текст из кривой», чтобы восстановить его в стандартное плоское текстовое поле.
Более простой способ создания идеальных форм с помощью формул — Изучите ЧПУ
В этом кратком совете я покажу вам, как сделать простой прямоугольник вокруг вашей работы, но на одинаковом расстоянии по всему периметру. И это на самом деле проект, в котором я только что помог кому-то. Они хотели сделать разделочные доски разного размера, с канавкой для сока, ровно в трех четвертях дюйма от края разделочной доски.
И для его конкретного проекта каждая доска была разного размера. Поэтому для каждого ему приходилось переделывать файл. Поэтому я показал ему быстрый способ сделать этот прямоугольник точно таким же расстоянием. И это, перейдя к инструменту прямоугольника. И в этом случае мы обнуляем нижний левый угол. Так что это наша точка отсчета для 0,0.
Итак, для нашей опорной точки мы собираемся сделать тот же нижний левый угол, и мы хотим, чтобы эта линия была на расстоянии трех четвертей дюйма по X и Y. Итак, мы собираемся ввести 0,75 дюйма для обоих из этих чисел. Это начнет наш прямоугольник в трех четвертях дюйма от края, и нам нужны прямые углы.
А для ширины и высоты вы будете использовать формулу вместо того, чтобы пытаться вычислить это число вручную. Таким образом, для нашей общей ширины минус граница в три четверти дюйма с обеих сторон будет нашей шириной минус полтора дюйма. Кроме того, если у вас было число нечетного размера для этих трех четвертей, я покажу вам, как это сделать.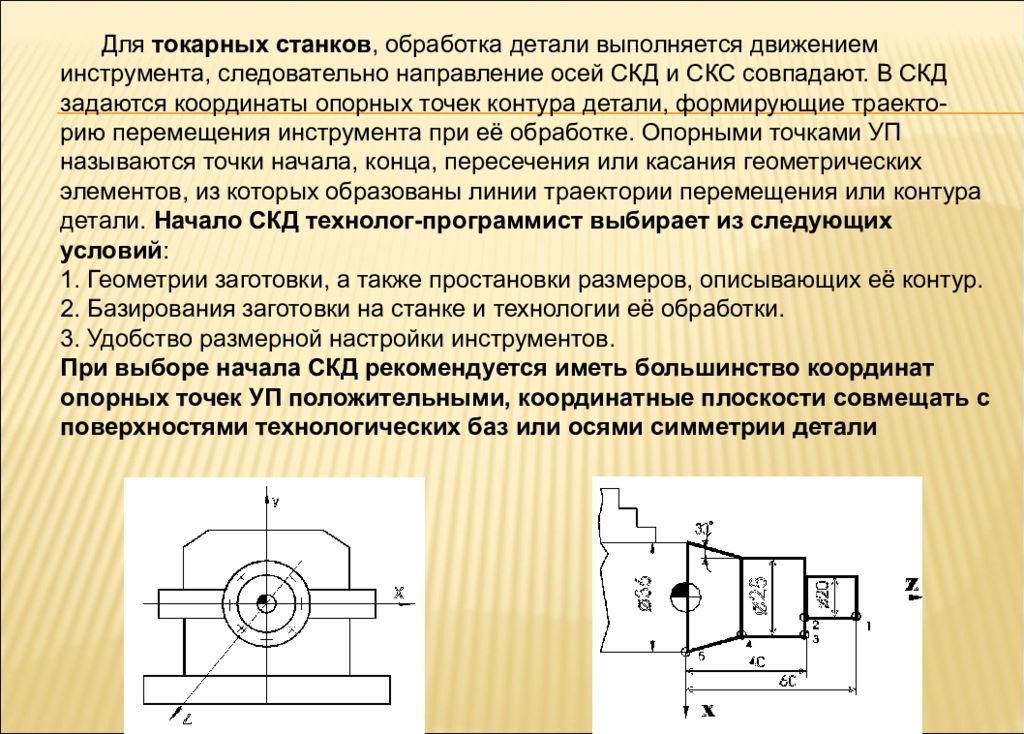
Итак, для ширины вы должны ввести здесь формулу. Таким образом, вы можете либо ввести букву W для ширины, либо букву X для измерения X. Обе эти переменные дадут вам один и тот же результат. Итак, это первая часть нашего уравнения. Наша следующая часть нашего уравнения — мы хотим вычесть. Граница раза два.
Итак, если ваша граница представляет собой простое число, например, три четверти дюйма, мы уже знаем, что умножить два на полтора. Таким образом, вы бы сделали X минус полтора. Но если это было нечетное число, и вы не знали точно, какое это удвоение, вы можете поставить Х, а затем минус, а затем в скобках вы бы сделали 0,75, что является нашим граничным временем, которое является маленьким знаком умножения. число два, а затем закройте скобки. Таким образом, общая формула равна X, что является нашей шириной минус граница, умноженная на два. И затем, в самом конце, вы нажмете равно. И это даст вам вашу формулу. Так что вы можете это сделать. Также для высоты вы сделаете то же самое.
Итак, в этом случае вы должны написать букву H для высоты или букву Y для размера Y. И мы могли бы использовать ту же самую формулу, которую мы только что сделали. Или, как я сказал, если бы вы знали двойное число, которое в данном случае три четверти, умноженное на два, составляет полтора, вы бы сделали Y минус 1,5. А потом знак равенства, и это даст вам ответ.
А теперь, если мы нажмем кнопку «Создать», этот прямоугольник теперь будет ровно в трех четвертях дюйма от края по всему периметру. Так что это очень быстрый способ сделать прямоугольники именно того размера, который вам нужен, в соответствии с шириной и высотой вашей формы. И я бы также рекомендовал поместить их на отдельный слой.
И свяжите этот слой с траекторией, если можете. Итак, как вы могли видеть в этом примере, мы создали шаблон траектории, который мы просто загружаем сюда, и это будет верхняя сторона. Нажмите «Открыть», и я применю его только к этому листу, и на самом деле мне просто нужно пересчитать их для этого конкретного листа.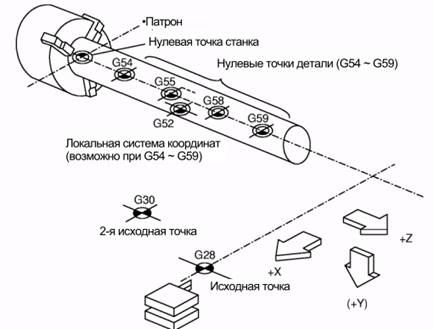

Всего комментариев: 0