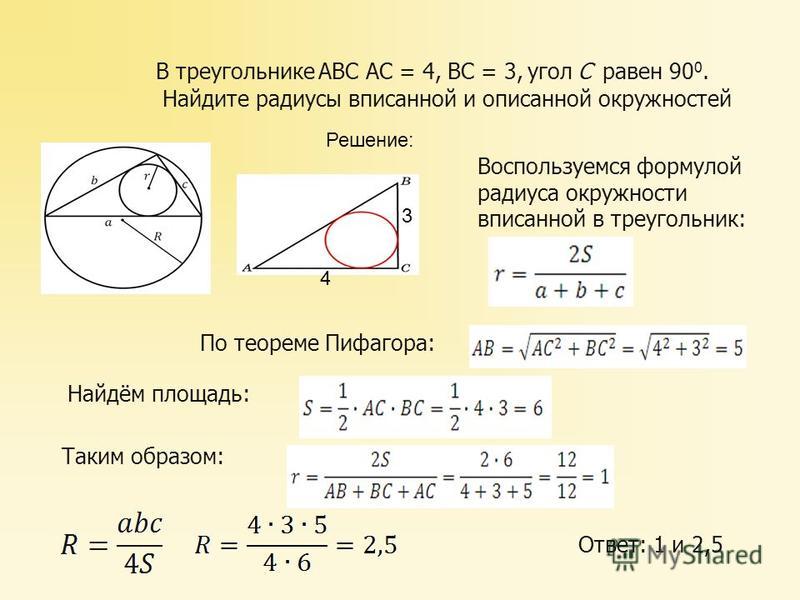
Найти известные углы абс: Дан треугольник абс ,а=35,с=45,найти угол б
Содержание
Теорема косинусов и синусов треугольника. Формулы и примеры
9 класс — насыщенное новыми знаниями время. Чтобы не запутаться в теории по геометрии, рекомендуем сделать карточки с информацией по каждой теме. В этой статье вы найдете самое важное про теорему косинусов.
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a2> + b2> = c2>, где a, b — катеты, с — гипотенуза.
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними. Формула теоремы косинусов: a2 = b2 + c2 — 2bc cos α |
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
BC2 = (x2 — x1)2 + (y2 — y1)2
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
cos2α + sin2α = 1 — основное тригонометрическое тождество.
BC2 = a2 = (b cos α — c)2 + b2sin2α = b2cos2α + b2sin2α — 2bc cos α + c2 = b2(cos2α + sin2α) — 2bc cos α + c2
Что и требовалось доказать.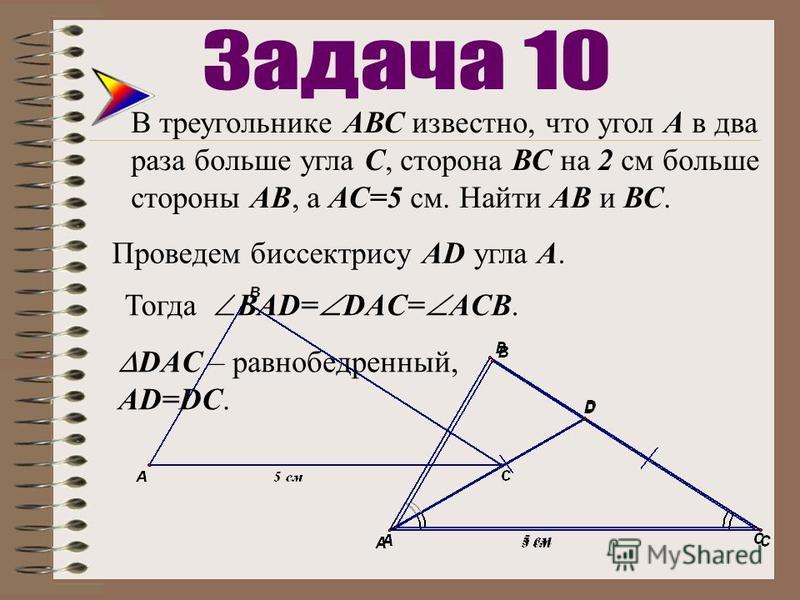
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на
онлайн-курсы по математике для детей и подростков.
С помощью теоремы косинусов можно найти косинус угла треугольника:
- Когда b2 + c2 — a2 > 0, угол α будет острым.
- Когда b2 + c2 — a2 = 0, угол α будет прямым.
- Когда b2 + c2 — a2 < 0, угол α будет тупым.
Запоминаем
Когда угол α прямой, то теорема косинусов превращаеся в теорему Пифагора.
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b × cos α,
- DB = c – b × cos α.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h2 = b2 — (b × cos α)2
- h2 = a2 — (c – b × cos α)2
Приравниваем правые части уравнений:
- b2 — (b × cos α)2 = a2 — (c — b × cos α)2
либо
- a2 = b2 + c2 — 2bc × cos α
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
- b2 = a2 + c2 — 2ac × cos β;
- c2 = a2 + b2 — 2ab × cos γ.
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a2 = b2 + c2 — 2bc cos α
b2 = c2 + a2 — 2ca cos β
c2 = a2 + b2 — 2ab cos γ
Теорема косинусов может быть использована для любого вида треугольника.
Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Аналогично:
Бесплатные занятия по английскому с носителем
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Определение угла с помощью косинуса
А теперь обратим внимание на углы.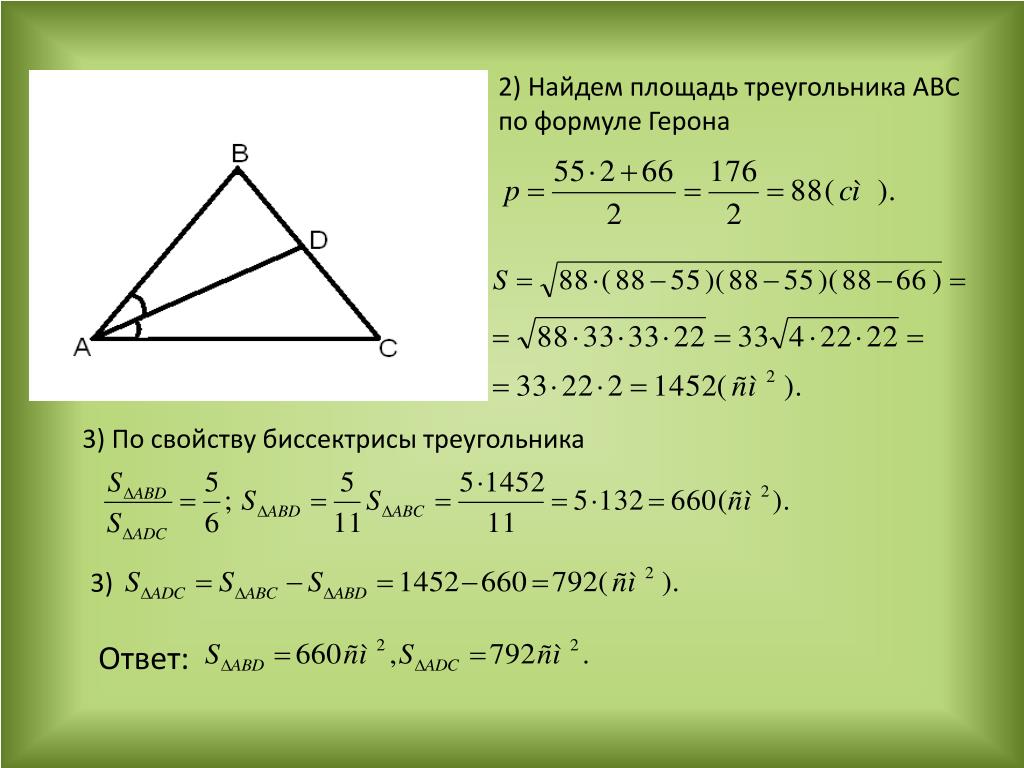
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Предел изменения косинуса: -1 < cos α < 1.
Предел изменения синуса: 0 < sin α ≤ 1.
- Если cos α > 0, то α ∈ (0°;90°)
- Если cos α < 0, то α ∈ (90°;180°)
- Если cos α = 0, то α = 90°
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
Как решаем:
- Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B: - Из треугольника СМВ по теореме косинусов найдём СМ:
Ответ: СМ = .
Пример 2. Дан треугольник АВС, в котором a2 + b2 < c2. Доказать, что ∠C — тупой угол.
Как доказываем:
- Для доказательства нужно вспомнить теорему косинусов для угла ∠C:
- Так как a2 + b2 < c2, то cos C < 0, следовательно, ∠C — тупой.

Что и требовалось доказать.
Эта задача нам показала, что с помощью теоремы косинусов можно определить тупой угол или острый.
- Если c2 = a2 + b2, то ∠C = 90°.
- Если c2 < a2 + b2, то ∠C — острый.
Больше объяснений по этой и другим темам вы найдете в справочнике по математике — с формулами, чертежами и примерами решения задач.
Шпаргалки по математике родителей
Все формулы по математике под рукой
Урок геометрии в 7-м классе по теме «Сумма углов треугольника»
На изучение материала параграфа “Сумма углов треугольника” отводится три
урока. Это первый урок, на котором рассматривается одна из важнейших теорем
курса геометрии 7-го класса – теорема о сумме углов треугольника. В 6-ом классе,
обучаясь по учебному комплекту Дорофеева Г. В., учащиеся выполняли практическую
В., учащиеся выполняли практическую
работу на вычисление суммы углов треугольника с помощью транспортира, и
значительная часть учащихся получила результат, отличный от 180°. В
рассматриваемой на уроке теореме формулируется неочевидный геометрический факт,
который в ходе урока будет доказан различными способами. На уроке важен процесс
размышления, поиска ответа. Запланирована активная исследовательская
деятельность учащихся. У учителя роль дирижёра. Система вопросов учителя
позволяет учащимся осуществить поиск доказательства теоремы, рассмотреть
возможности её обобщения. С доказательством теоремы, предлагаемым автором
учебника Атанасяном Л.С., учащиеся знакомятся в ходе самостоятельной работы с
учебником. Решение задач на применение теоремы предполагает закрепление
полученных в 6-ом классе умений находить неизвестные углы треугольника. Все
пояснения учащиеся дают устно, обучение записи решения – это задача следующего
урока.
Тип урока: урок изучения нового материала,
урок-исследование.
Цели урока:
- рассмотреть различные способы доказательства теоремы о сумме углов
треугольника, рассмотреть возможность обобщения теоремы и ее применение для
нахождения неизвестных углов треугольника по двум известным или одному
известному углу; - формировать логическое мышление, развивать речь учащихся, внимание,
познавательный интерес; - формировать позитивное отношение к новому учебному предмету, умение
давать полный и грамотный ответ на поставленный вопрос, умение слушать,
умение самостоятельно готовить ответ в ходе работы с учебником.
Оборудование: компьютер, мультимедийный проектор, презентация
(приложение1), линейка.
Ход урока
- Постановка учебной задачи
Какие утверждения, связанные с этой величиной (на слайде – 180°), вам
известны?
- Развернутый угол равен 180°.

- Сумма смежных углов равна 180°.
- Сумма односторонних углов при параллельных прямых равна 180°.
- Сумма углов треугольника равна 180°.
Учащимся предлагается в тетрадях записать число, “ Классная работа” и тему
урока: “Сумма углов треугольника” (слайд с названием темы урока).
В 6-м классе мы проводили эксперимент, измеряя транспортиром углы и вычисляя
их сумму для различных треугольников. В результате выдвинули гипотезу о том, что
сумма углов треугольника равна 180° (по щелчку на том же слайде утверждение о
сумме углов треугольника появляется полностью).
Автор учебника Григорий Владимирович Дорофеев предлагал вариант рассуждений,
подтверждающий справедливость выдвинутой гипотезы. Но его рассуждения не были
полными. Сегодня вы имеете достаточно знаний для того, чтобы заполнить имеющиеся
пробелы.
Скажите, пожалуйста, как называется утверждение, справедливость которого
устанавливается с помощью доказательства? Теорема.
Учитель на доске пишет слово “Теорема”, а учащиеся в тетрадях записывают и
это слово, и формулировку теоремы.
Задачи урока:
- доказать теорему о сумме углов треугольника, попытаться её обобщить,
рассмотреть её применение к решению задач на нахождение неизвестных углов
треугольника.
- Актуализация опорных знаний
Для доказательства теоремы будут необходимы некоторые теоретические
положения. Вспомним их, выполняя следующие задания.
Задания на слайдах (в ходе ответов на слайдах по щелчку происходят
соответствующие изменения):
- Доказательство теоремы
Выделим условие и заключение теоремы: что дано и что требуется доказать.
Учитель на доске, а учащиеся в тетрадях изображают треугольник АВС и
выполняют соответствующие записи.
Чтобы найти сумму углов треугольника, их надо сложить. Поэтому пойдём
естественным путём: будем углы складывать.
На слайде треугольник АВС. В ходе обсуждения на слайде по щелчку будут
происходить соответствующие изменения.
- Отложим углы А и С от сторон угла В (по разные стороны от него). Получим
угол МВN. Нужно доказать, что он равен180°, то есть является развёрнутым.
Рассмотрим углы 1 и 3. Какой вывод можно сделать? На каком основании? (ВМ
АС).
- Рассмотрим углы 2 и 4. Какой вывод можно сделать? На каком основании?
(ВN АС).
- Имеем: через точку В проходят две прямые, параллельные прямой АС.
Возможно ли это? На каком основании это можно утверждать? (Невозможно. Об
этом говорит аксиома параллельных).
Следовательно, прямые ВМ и ВN совпадают. МN
АС.
Следовательно, угол МВN развёрнутый, равен 180°.
С другой стороны, угол МВN равен сумме углов 3, 4, 5, то есть углов А, В, С –
углов данного треугольника. Можно ли доказательство упростить?
Угол С можно было и не откладывать. Как вы это можете объяснить? (Он “сам”
отложился).
Рассмотрим углы 1 и 3. Какой вывод можно сделать? На каком основании? (ВМ
АС).
Получили развёрнутый угол, составленный из углов 3, 4, 5, соответственно
равных углам треугольника АВС.
Следующий слайд демонстрирует второй способ доказательства теоремы. В ходе
обсуждения по щелчку происходят соответствующие изменения.
И, наконец, угол 4 можно даже не рассматривать.
- Рассмотрим углы 1 и 3. Какой вывод можно сделать? На каком основании? (ВМ
АС). - Рассмотрим угол МВС и угол С треугольника. Какой вывод можно сделать? На
каком основании? (Их сумма равна 180°).
Угол МВС равен сумме углов 3 и 5, соответственно равных углам А и В
треугольника. Таким образом, сумма углов треугольника равна 180°.
Таким образом, сумма углов треугольника равна 180°.
Мы практически рассмотрели три способа доказательства теоремы.
Первое доказательство выявляет ведущую роль аксиомы параллельных прямых,
второе и третье используют признак параллельности прямых и свойства углов при
параллельных прямых.
Автор нашего учебника Левон Сергеевич Атанасян предлагает идти другим путем:
он через одну из вершин треугольника проводит прямую, параллельную
противоположной стороне, и разлагает полученный развёрнутый угол на углы, равные
углам треугольника.
Используется обратная операция: разложение угла на три угла.
Учитель на доске, а учащиеся в тетрадях через точку В проводят прямую a,
параллельную прямой АС. Затем учащимся предлагается поработать с доказательством
теоремы по учебнику и в результате представить его у доски. Обращается внимание
учащихся на то, что в учебнике иначе расставлены цифры, обозначающие углы, так
как логика рассуждений несколько иная. Заслушав кого-либо из учащихся у доски,
Заслушав кого-либо из учащихся у доски,
учитель на доске, а учащиеся в тетрадях (по образцу учителя) записывают
доказательство теоремы.
Это четвёртый способ доказательства теоремы. Есть и пятый, о котором сегодня
уже говорилось.
Учащимся предлагается дома восстановить полностью доказательство теоремы,
предлагаемое автором учебника по математике для 6 класса Дорофеева Г.В. Это
задание для желающих. На перемене у учителя можно получить рисунок к этому
способу доказательства. Этот рисунок демонстрируется и на слайде.
- Обобщение теоремы
- Как обобщить теорему? Выявим объект, который есть в теореме. Это
треугольник. Заменим треугольник другим объектом и сформулируем новое
утверждение. - Рассмотрим вместо треугольника четырёхугольник. Что надо найти? Найти
нужно сумму углов четырёхугольника. Какие будут предложения?
Какие будут предложения?
Следующий слайд демонстрирует обобщение теоремы для четырёхугольника. В
ходе обсуждения по щелчку происходят соответствующие изменения.
Рассмотрим теперь пятиугольник. Найдем сумму его углов.
Следующий слайд демонстрирует обобщение теоремы для пятиугольника. В ходе
обсуждения по щелчку на слайде происходят соответствующие изменения.
Выслушать предложения учащихся, обсудить два способа определения суммы углов
пятиугольника, а третий предложить для домашней самостоятельной работы.
Можно пойти дальше, что мы и сделаем в 8-ом классе, доказав, что сумма углов
выпуклого многоугольника, у которого n углов, можно получить, умножив 180° на
(n-2).
Следующий слайд посвящён сумме углов выпуклого n-угольника.
При n =3; 4; 5 будем иметь уже полученные результаты.
Учащиеся устно выполняют вычисления по предложенной формуле для
треугольника, четырёхугольника и пятиугольника.
- Применение теоремы к решению задач на нахождение неизвестных углов
треугольника
Требуется найти неизвестные углы.
Задачи предлагаются на слайдах. В ходе решения задач на слайдах по щелчку
происходят соответствующие изменения.
- В задаче № 1требуется найти неизвестный угол треугольника по двум
известным углам. - В задаче № 2 требуется найти неизвестные углы треугольника, имея лишь
один известный угол. Тем не менее задача разрешима. Учащимся предлагается
обосновать этот момент. - В задаче № 3 ситуация аналогична предыдущей.
- В задаче № 4 вообще нет известных углов, но есть определённая
зависимость между углами треугольника. В результате решения задачи имеем
треугольник, один из углов которого равен 90°. Учащимся предлагается дать
название угла, равного 90°, и соответственно назвать треугольник.
И в заключение предлагаю обдумать следующую ситуацию (задание для
самостоятельных размышлений дома).
Летели на корабле, сгорела часть карты. Нужно найти угол между двумя прямыми
(от этого зависит жизнь тех, кто летел на корабле).
Вниманию учащихся предлагается слайд с исходной ситуацией. Задание учащиеся
записывают в тетрадь для домашней работы.
- Подведение итога урока
Сегодня мы работали с одной из важнейших теорем геометрии. О чём она говорит
и какую возможность нам предоставляет?
По гиперссылке переходим на слайд, где дана формулировка теоремы.
Вы должны уметь доказывать теорему о сумме углов треугольника и применять её
к решению задач на нахождение неизвестных углов треугольника.
- Домашнее задание
п.30, с.89 в.1, №№ 223, 225, 229, задание в тетради.
Презентация
Комплексные числа: углы и полярные координаты
Комплексные числа: углы и полярные координаты
Этот раздел предполагает знание тригонометрии. Для получения информации о тригонометрии см. Краткий курс Дейва по триггерам на
http://www.clarku.edu/~djoyce/trig/
Полярные координаты помогут нам понять комплексные числа геометрически. С одной стороны, обычные прямоугольные координаты
x и y задают комплексное число z = x + yi , указав расстояние
x вправо и расстояние y вверх. С другой стороны, полярные координаты определяют ту же точку z , говоря, как
far r от начала координат 0 и угол для линии от начала координат до точки.
Мы уже назвали расстояние r абсолютной величиной | из | z, , и мы увидели, как
Теорема Пифагора установила связь между ним и х и и :
Далее нам нужно разобраться с углом . Мы будем следовать стандартному соглашению для указания угла
Мы будем следовать стандартному соглашению для указания угла
. Согласно этому соглашению положительная ось x (наша реальная ось) проходит под углом 0°, т.е.
положительная ось y (наша воображаемая ось) под углом 90°, отрицательная ось x под углом 180° и отрицательная
y — ось под углом 270°. Кроме того, 360° можно добавить или вычесть из любого угла, и направление не изменится. Так,
0°, 360°, 720° и 360° относятся к положительному x — ось. Аналогично, 270° и 90°
оба относятся к отрицательной оси y . Угол 45° проходит вдоль линии y = x , вверх вправо.
И так далее.
Точка z может быть задана любой парой, парой прямоугольных координат, x и y , или парой полярных координат.
координаты, р, что | z | и , который является arg ( z ). Поскольку любая пара
определяет точку,
каждая пара должна определять другую пару. Должно быть четыре уравнения, связывающих их, и так есть. Пифагорейский
Должно быть четыре уравнения, связывающих их, и так есть. Пифагорейский
тождество было упомянуто выше, но остальные требуют тригонометрии. Из того же треугольника мы
используемые для теоремы Пифагора, мы находим следующие три соотношения:
tan = y/x , x = r cos , и
y = r sin .
Теперь, если мы применим эти отношения к нашему комплексному числу z = x + yi, , то мы получим
альтернативное описание для z
| с | = | x + iy |
| = | r cos + i r sin | |
| = | r (cos + i sin ) | |
| = | | из | (cos + i sin ) |
Обратите внимание, что комплексное число cos + i sin имеет абсолютное значение 1, поскольку cos 2 + sin 2 равно 1 для любого угла . Таким образом, каждое комплексное число z является
Таким образом, каждое комплексное число z является
произведение действительного числа | г | и комплексное число cos + i sin .
Мы почти подошли к тому моменту, когда можем доказать последнее недоказанное утверждение предыдущего раздела об умножении, а именно,
что arg( zw ) = arg( z ) + arg( w ). Как и выше, мы принимаем arg( z ) как , а теперь пусть arg( w ) будет . Затем,
z = | из | (кос + я грех)
а также
w = | с | (кос + я грех)
Нам нужно показать, что arg( zw ) равно + . Другими словами
zw = | ZW | (cos ( + ) + i sin
( + ))
Если мы воспользуемся формулами сложения для косинуса и синуса в одном важном моменте, мы его получим. Напомним из тригонометрии эти сложения
формулы:
потому что ( + ) = потому что
cos sin sin
sin ( + ) = cos sin + sin cos .
Теперь мы готовы показать аргументы, добавленные в продукт zw.
| цв | = | | из | (cos + i sin ) | с | (потому что + я грех ) |
| = | | ZW | (cos + i sin ) (cos + i sin ) | |
| = | | ZW | ((cos cos sin sin ) + i (cos sin + sin cos )) | |
| = | | ZW | (cos ( + ) + i sin ( + )) |
Таким образом, arg( zw ) равно + , как и утверждалось.
С# — Как рассчитать угол между линией и горизонтальной осью?
Сначала найдите разницу между начальной и конечной точками (здесь это скорее направленный отрезок, а не «линия», поскольку линии простираются бесконечно и не начинаются в какой-то конкретной точке).
дельтаY = P2_y - P1_y дельтаX = P2_x - P1_x
Затем вычислите угол (который проходит от положительной оси X в точке P1 до положительной оси Y в точке P1 ).
угол в градусах = арктангенс(дельтаY / дельтаX) * 180 / PI
Но арктангенс может быть не идеальным, потому что разделение разностей таким образом сотрет различие, необходимое для того, чтобы различить, в каком квадранте находится угол (см. ниже). Вместо этого используйте следующее, если ваш язык включает atan2 функция:
angleInDegrees = atan2(deltaY, deltaX) * 180/PI
РЕДАКТИРОВАТЬ (22 февраля 2017 г.): Однако в целом вызов atan2(deltaY,deltaX) только для того, чтобы получить правильный угол для cos и sin , может быть неэлегантным. В таких случаях часто можно сделать следующее:
- Обработать
(дельтаX, дельтаY)как вектор. - Нормализуйте этот вектор к единичному вектору.
 Для этого разделите
Для этого разделите deltaX наиdeltaYпо длине вектора (sqrt(deltaX*deltaX+deltaY*deltaY)), если длина не равна 0. - После этого
deltaXтеперь будет косинусом угла между вектором и горизонтальной осью (в направлении от положительной оси X к положительной оси Y в точкеP1). - и
deltaYтеперь будут синусом этого угла. - Если длина вектора равна 0, у него не будет угла между ним и горизонтальной осью (поэтому у него не будет осмысленных синуса и косинуса).
EDIT (28 февраля 2017 г.): даже без нормализации (deltaX, deltaY) :
- Знак
deltaXскажет вам, является ли косинус, описанный в шаге 3, положительным или отрицательным. - Знак
deltaYпокажет вам, является ли синус, описанный в шаге 4, положительным или отрицательным. - Знаки
deltaXиdeltaYподскажут, в каком квадранте находится угол относительно положительной оси X в точкеР1:-
+deltaX,+deltaY: от 0 до 90 градусов.
-
-deltaX,+deltaY: от 90 до 180 градусов. -
-deltaX,-deltaY: от 180 до 270 градусов (от -180 до -90 градусов). -
+deltaX,-deltaY: от 270 до 360 градусов (от -90 до 0 градусов).
-
Реализация на Python с использованием радианов (предоставлена 19 июля 2015 г. Эриком Лещински, который отредактировал мой ответ):
из математического импорта *
определение угла_trunc (а):
в то время как а < 0,0: а += пи * 2 вернуть def getAngleBetweenPoints (x_orig, y_orig, x_landmark, y_landmark): deltaY = y_ориентир - y_orig deltaX = x_ориентир - x_orig вернуть angle_trunc (atan2 (deltaY, deltaX)) угол = getAngleBetweenPoints (5, 2, 1,4) утверждать угол >= 0, "угол должен быть >= 0"
угол = получить угол между точками (1, 1, 2, 1)
утверждать угол == 0, "ожидается, что угол будет равен 0"
угол = получить угол между точками (2, 1, 1, 1)
assert abs(pi - angle) <= 0.

Всего комментариев: 0