Найти известные углы абс: Найдите углы треугольника ABC, если ∠A:∠B:∠C= 2:3:4.

Сумма углов треугольника: чему равна и как найти?

Доказательство теоремы:

Нарисуем треугольник. Через одну из его вершин проведем прямую, параллельную противоположной стороне, и найдем на рисунке равные углы.

Угол 1 равен углу BAC, они накрест лежащие. Угол 2 равен углу ACB, они тоже накрест лежащие.

Сумма угла 1, угла ABC и угла 2 составляет развернутый угол.

A развернутый угол равен . Значит, и сумма углов треугольника тоже равна 180 градусов.

Разберем задачи ЕГЭ и ОГЭ, в которых фигурирует сумма углов треугольника.

Заметим, что они похожи друг на друга. Одна и та же задача на тему «Сумма углов треугольника» может встретиться и на ОГЭ, и на ЕГЭ по математике. И уровень сложности заданий по этой теме в ЕГЭ и ОГЭ примерно одинаковый.

Задачи ЕГЭ по теме: Сумма углов треугольника

Задача 1. Один из внешних углов треугольника равен 85 градусов. Углы, не смежные с данным внешним углом, относятся как 2:3. Найдите наибольший из них. Ответ дайте в градусах.

Решение:

Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Следовательно, сумма двух других углов треугольника равна 85 градусов, а их отношение равно 2:3. Пусть эти углы равны 2х и 3х.

Получим уравнение:

 и найдем x = 17.

Тогда .

Ответ: 51.

Обратите внимание, что это даже не геометрия, а алгебра. Мы составили уравнение и решили его.

Задача 2.

Один из углов равнобедренного треугольника равен 98 градусов. Найдите один из других его углов. Ответ дайте в градусах.

Решение:

Как вы думаете, может ли равнобедренный треугольник иметь два угла по 98 градусов?

Нет, конечно! Ведь сумма углов треугольника равна 180 градусов. Значит, один из углов треугольника равен , а два других равны .

Ответ: 41.

Задача 3.

На рисунке угол 1 равен , угол 2 равен , угол 3 равен . Найдите угол 4. Ответ дайте в градусах.

Решение:

Давайте отметим на чертеже еще несколько углов.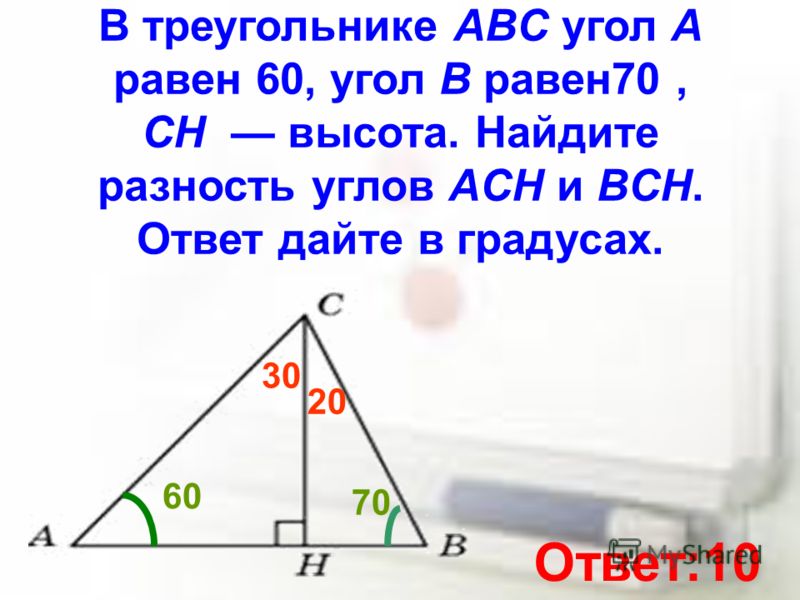 Они нам понадобятся.

Сначала найдем угол 5.

Он равен

Тогда

Угол 4, смежный с углом 7 равен

Ответ:

Заметим, что такой способ решения — не единственный. Просто находите и отмечайте на чертеже все углы, которые можно найти.

Задача 4.

Углы треугольника относятся как . Найдите меньший из них. Ответ дайте в градусах.

Решение:

Пусть углы треугольника равны 2x, 3x и 4x. Запишем, чему равна сумма углов этого треугольника.

Тогда

Здесь мы тоже составили уравнение и решили его. Так же, как на уроках алгебры.

Ответ: 40.

Задача 5. В треугольнике ABC проведена биссектриса AL, угол ALC равен , угол ABC равен . Найдите угол ACB. Ответ дайте в градусах.

Решение:

ALC — внешний угол и он равен сумме двух внутренних углов, не смежных с ним. Значит, .

AL — биссектриса , а это значит, что .

По теореме о сумме углов треугольника получаем:

Ответ: 125.

Задача 6. В выпуклом четырёхугольнике ABCD известно, что AB=BC, AD=CD, B=61D=151 Найдите величину угла A. Ответ дайте в градусах.

Решение:

Если соединить точки B и D, получим два равных треугольника. Они равны по трем сторонам. В равных треугольниках напротив равных сторон лежат равные углы.

В треугольнике ABD сумма двух углов

Тогда , по теореме о сумме углов треугольника.

Ответ: 74.

Задача 7. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен . Найдите вписанный угол ACB. Ответ дайте в градусах.

Решение:

AC и BD — диаметры окружности. Значит, — равнобедренный, в нем — как радиусы.

как вертикальные углы, тогда по теореме о сумме углов в треугольнике:

.

Ответ: 28.

Задача 8. В треугольнике ABC AD — биссектриса, угол C равен , угол CAD равен . Найдите угол B. Ответ дайте в градусах.

Решение:

AD — биссектриса, отсюда следует, что .

Тогда по теореме о сумме углов треугольника .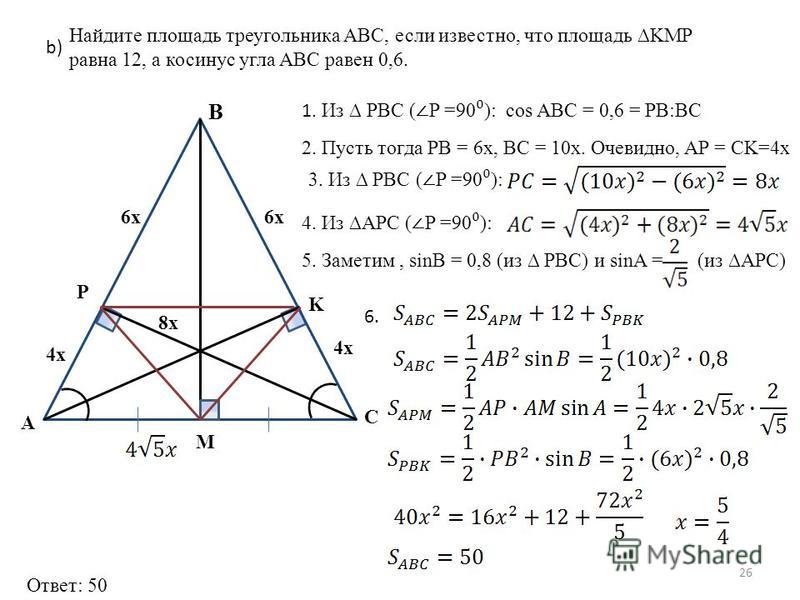

Ответ: 66.

Задача 9. В треугольнике ABC CD — медиана, угол C равен , угол B равен . Найдите угол ACD. Ответ дайте в градусах.

Решение:

В треугольнике ABC угол C равен , угол B равен , тогда угол A равен .

CD — медиана. А медиана, проведенная к гипотенузе в прямоугольном треугольнике, равна половине гипотенузы. Значит, .

Поэтому треугольник ADC равнобедренный и .

Ответ: 55.

Задача 10. В треугольнике ABC угол C равен , биссектрисы AD и BE пересекаются в точке O. Найдите угол AOB. Ответ дайте в градусах

Решение:

В треугольнике ABC угол C равен , отсюда по теореме о сумме углов треугольника .

Биссектрисы AD и BE пересекаются в точке O. Угол OAB — это половина угла CAB, угол OBA — это половина угла CBA. Теперь применим теорему о сумме углов треугольника к треугольнику AOB.

Ответ: 119.

Задача 11. В треугольнике ABC угол A равен , углы B и C — острые, высоты BD и CE пересекаются в точке O. Найдите угол DOE. Ответ дайте в градусах.

Решение:

BD — высота тогда — прямоугольный,

CE — высота тогда — прямоугольный и .

Углы и — смежные, поэтому .

Ответ: 124.

Задача 11. В прямоугольном треугольнике угол между высотой и биссектрисой, проведёнными из вершины прямого угла, равен . Найдите меньший угол прямоугольного треугольника. Ответ дайте в градусах.

Решение:

Обозначим на рисунке вершины треугольника ABC, биссектрису CК и высоту CН. Биссектриса CК делит прямой угол на два угла по . Угол BCН равен разности углов BCК и КCН, то есть .

Треугольники BCН и BAC подобны по двум углам. Значит, угол BAC равен углу BCН, то есть

Ответ: 31.

Задача 12. Острые углы прямоугольного треугольника равны и . Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

Решение:

Обозначим на рисунке медиану CМ и высоту CН.

Пусть и . Высота CН разбивает прямоугольный треугольник на два треугольника, подобных исходному. Значит, угол BCН равен углу BAC, то есть .

у которых углы равны т. е. угол C разбился на углы

и

Медиана, проведенная к гипотенузе в прямоугольном треугольнике, равна половине гипотенузы. Получили два равнобедренных треугольника, BCМ и ACМ. В треугольнике ACМ углы A и C равны 6 градусов каждый.

Тогда угол МCН между высотой и медианой равен:

Ответ: 78.

Задачи ОГЭ по математике по теме: Сумма углов треугольника.

Задача 13. В треугольнике два угла равны и . Найдите его третий угол. Ответ дайте в градусах.

Решение:

Сумма углов в треугольнике равна , поэтому

третий угол равен .

Ответ: 37.

Задача 14. Один из острых углов прямоугольного треугольника равен 34. Найдите его другой острый угол. Ответ дайте в градусах.

Решение:

Сумма острых углов прямоугольного треугольника равна . Поэтому второй острый угол равен: .

Ответ: 56.

Задача 15.

В треугольнике ABC известно, что AB=BC, . Найдите угол BCA. Ответ дайте в градусах.

Решение:

В треугольнике ABC известно, что AB=BC. Значит, треугольник ABС равнобедренный, и углы при основании AС равны,

т.е. .

Ответ: 36.

Задача 16. В остроугольном треугольнике ABC проведена высота BH, . Найдите угол ABH. Ответ дайте в градусах.

Решение:

BH — высота , тогда — прямоугольный, в нем и Используя теорему о сумме углов в треугольнике, найдем угол ABH:

Ответ: 53.

Задача 17. В треугольнике ABC угол C равен . Найдите внешний угол при вершине C. Ответ дайте в градусах.

Решение:

Внешний угол треугольника AВC при вершине C является смежным углом с углом ACB, а сумма смежных углов равна .

Значит, внешний угол треугольника ABC при вершине C равен: .

Ответ: 47.

Задача 18. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и . Найдите угол BOC. Ответ дайте в градусах.

Решение:

— равнобедренный, .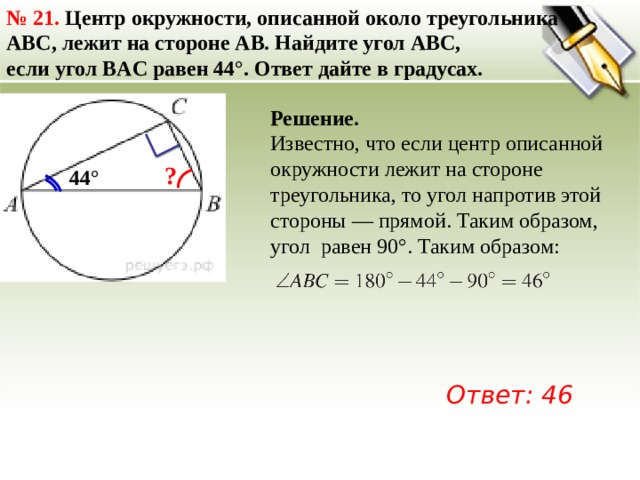

— вписанный угол и опирается на дугу BC, а — центральный угол и также опирается на дугу BC. Центральный угол в два раза больше вписанного опирающегося на ту же дугу, .

Ответ: 155.

Задача 19. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ABC=123. Найдите угол BOC. Ответ дайте в градусах.

Решение:

— равнобедренный треугольник, отсюда .

— вписанный угол, он опирается на дугу BC, а — центральный угол и также опирается на дугу BC. Центральный угол в два раза больше вписанного угла, опирающегося на ту же дугу, значит, .

Ответ: 57.

Задача 20. В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен . Найдите угол ACB. Ответ дайте в градусах.

Решение:

AC и BD — диаметры, отсюда следует, что — равнобедренный, — радиусы.

как вертикальные углы, тогда по теореме о сумме углов в треугольнике .

Ответ: 33.

Задача 21. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен . Ответ дайте в градусах.

Решение:

Центр окружности, описанной около треугольника ABC, лежит на стороне AB. A это означает, что AB — диаметр. Угол, опирающийся на диаметр, равен , и треугольник ABC — прямоугольный. И если , то второй острый угол этого треугольника равен:

Ответ: 15.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Сумма углов треугольника» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
07.04.2023

Теорема косинусов и синусов треугольника. Формулы и примеры

Поможем понять и полюбить математику

Начать учиться

244. 1K

9 класс — насыщенное новыми знаниями время. Чтобы не запутаться в теории по геометрии, рекомендуем сделать карточки с информацией по каждой теме. В этой статье вы найдете самое важное про теорему косинусов.

Формулировка и доказательство теоремы косинусов

Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Формула Теоремы Пифагора:

a²> + b²> = c²>, где a, b — катеты, с — гипотенуза.

В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:

BC² = (x₂ — x₁)² + (y₂ — y₁)²

В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).

cos²α + sin²α = 1 — основное тригонометрическое тождество.

BC² = a² = (b cos α — c)² + b²sin²α = b²cos²α + b²sin²α — 2bc cos α + c² = b²(cos²α + sin²α) — 2bc cos α + c²

Что и требовалось доказать.

Совет: чтобы быстрее разобраться в сложной теме, запишитесь на
онлайн-курсы по математике для детей и подростков.

С помощью теоремы косинусов можно найти косинус угла треугольника:

• Когда b² + c² — a² > 0, угол α будет острым.
• Когда b² + c² — a² = 0, угол α будет прямым.
• Когда b² + c² — a² < 0, угол α будет тупым.

Запоминаем

Когда угол α прямой, то теорема косинусов превращаеся в теорему Пифагора.

Сформулируем еще одно доказательство теоремы косинусов.

Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:

• AD = b × cos α,
• DB = c – b × cos α.

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

• h² = b² — (b × cos α)²
• h² = a² — (c – b × cos α)²

Приравниваем правые части уравнений:

• b² — (b × cos α)² = a² — (c — b × cos α)²

либо

• a² = b² + c² — 2bc × cos α

Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определим стороны b и c:

• b² = a² + c² — 2ac × cos β;
• c² = a² + b² — 2ab × cos γ.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Формулировка теоремы для каждой из сторон треугольника

Теорема косинусов справедлива для всех сторон треугольника, то есть:

a² = b² + c² — 2bc cos α

b² = c² + a² — 2ca cos β

c² = a² + b² — 2ab cos γ

Теорема косинусов может быть использована для любого вида треугольника.

Косинусы углов треугольника

Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:

Аналогично:

Определение угла с помощью косинуса

А теперь обратим внимание на углы.

Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).

Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.

Рассмотрение пределов изменения cos α и sin α

Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.

Предел изменения косинуса: -1 < cos α < 1.

Предел изменения синуса: 0 < sin α ≤ 1.

• Если cos α > 0, то α ∈ (0°;90°)
• Если cos α < 0, то α ∈ (90°;180°)
• Если cos α = 0, то α = 90°

Примеры решения задач

При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.

Пример 1. Дан треугольник АВС. Найти длину СМ.

∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

Как решаем:

1. Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
   Из треугольника АВС найдем cos B:

2. Из треугольника СМВ по теореме косинусов найдём СМ:

Ответ: СМ = .

Пример 2. Дан треугольник АВС, в котором a2  + b2 < c2. Доказать, что ∠C — тупой угол.

Как доказываем:

1. Для доказательства нужно вспомнить теорему косинусов для угла ∠C: 
2. Так как a²  + b² < c², то cos C < 0, следовательно, ∠C — тупой.

Что и требовалось доказать.

Эта задача нам показала, что с помощью теоремы косинусов можно определить тупой угол или острый.

• Если c² = a² + b², то ∠C = 90°.

• Если c² < a² + b², то ∠C — острый.

Больше объяснений по этой и другим темам вы найдете в справочнике по математике — с формулами, чертежами и примерами решения задач.

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

Теоремы, которые точно пригодятся на ЕГЭ

К следующей статье

158.7K

Векторное произведение векторов

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Как найти недостающий угол треугольника (видео и примеры) Пол Маццола

Углы треугольника

A треугольник – простейший из возможных многоугольников. Это двумерная (плоская) форма с тремя прямыми сторонами, образующими внутреннее замкнутое пространство. У него три внутренних угла . Одна из самых первых концепций, которую следует изучать в геометрии, заключается в том, что сумма внутренних углов треугольников равна 9.0017 180° . Но откуда ты знаешь? Как вы можете доказать, что это правда? Давай выясним!

Как найти угол треугольника

У вас может быть треугольник, в котором отмечены и измерены только два угла. Теперь, когда вы уверены, что внутренние углы всех треугольников в сумме составляют 180° , вы можете быстро вычислить недостающее измерение. Вы можете сделать это одним из двух способов:

1. Вычесть два известных угла из 180° .

2. Подставьте два угла в формулу и используйте алгебру: a+b+c=180°

Как найти недостающий угол треугольника

Два известных угла треугольника: 37° и 24° . Каков недостающий угол?

Мы можем использовать два разных метода, чтобы найти наш недостающий угол:

Как найти угол треугольника

Вычесть два известных угла из 180° :

Подставить два угла в формулу и использовать алгебру:  a + b + c = 180°

Формула угла треугольника

Нарисуем треугольник и обозначим его внутренние углы тремя буквами: a , b и c . Наш образец будет иметь сторону ac по горизонтали внизу и ∠b  наверху.

Теперь, когда мы обозначили наши углы, у нас есть формула, на которую мы можем ссылаться для углов. Это  a + b + c = 180° , что говорит нам о том, что если мы сложим все наши углы, они всегда будут равны 9.0017 180 .

Теперь давайте проведем линию, параллельную стороне ac , которая проходит через точку b (где вы также найдете ∠b ).

Теорема о чередующихся внутренних углах Чтобы найти недостающий угол в треугольнике

Эта новая параллельная прямая создала два новых угла по обе стороны от ∠b . Мы обозначим эти два угла ∠z и ∠w слева направо. Сторону ab нашего треугольника теперь можно рассматривать как поперечную, линию, пересекающую две параллельные линии.

Теорема о чередующихся внутренних углах

По теореме о альтернативных внутренних углах мы знаем, что ∠a сравнимо (равно) ∠z , а ∠c 900 18 соответствует ∠w .

Мы тебя потеряли? Не отчаивайся! Теорема о чередующихся внутренних углах говорит нам, что поперечное сечение двух параллельных прямых создает конгруэнтные альтернативные внутренние углы. Чередующиеся внутренние углы лежат между параллельными прямыми по разные стороны от секущей. В нашем примере ∠a и ∠z являются альтернативными внутренними углами, а также ∠c и ∠w .

Теперь у нас есть три угла нашего треугольника, тщательно перерисованные и имеющие общую точку Point b . У нас есть ∠z в качестве замены для ∠a , затем ∠b и, наконец, ∠w в качестве замены для ∠c . И посмотрите, они образуют прямую линию!

Прямая измеряет 180° . Это тот же тип доказательства, что и доказательство параллельных прямых. Три угла любого треугольника всегда дают в сумме 180° или прямая линия.

Теорема о сумме углов треугольника

Наша формула для этого: — внутренние углы любого треугольника.

Сумма углов треугольника равна 180° доказательство

Для выполнения этого удивительного математического трюка вам понадобятся четыре вещи. Вам понадобится линейка, ножницы, бумага и карандаш. На листе бумаги нарисуйте аккуратный большой треугольник. Любой треугольник — разносторонний, равнобедренный, равносторонний, остроугольный, тупоугольный — какой угодно.

Пометьте внутренние углы (вершины, образующие внутренние углы) тремя буквами, например  R-A-T . Вырежьте треугольник, оставив небольшую рамку вокруг него, чтобы вы могли видеть все три края.

Теперь оторвите три угла вашего треугольника. Не используйте ножницы, потому что вам нужны зубчатые края, которые помогут вам не перепутать их с прямыми сторонами, которые вы нарисовали. У вас будет три меньших треугольных бита, каждый с внутренним углом, обозначенным  R ,  A или T . Каждый маленький кусочек имеет две аккуратные стороны и шероховатый край.

У вас также будет грубый шестиугольник, который является оставшейся частью исходного большого треугольника.

Возьмите три маленьких отмеченных уголка и сложите их вместе так, чтобы необработанные края были далеко от вас. Единственный способ сделать это — заставить их выстроиться в прямую линию. Три внутренних угла RAT в сумме образуют прямой угол, также называемый прямой линией.

Есть; ты сделал это!

Резюме урока

Если вы внимательно изучили этот урок, то теперь вы можете определить и обозначить три внутренних угла любого треугольника, и вы можете вспомнить, что сумма внутренних углов всех треугольников составляет

Что вы узнали:

С помощью этого видео и урока вы научились:

• Определять и обозначать три внутренних угла любого треугольника

• Вспомнить, что сумма внутренних углов всех треугольников составляет 180°

• Продемонстрировать доказательство суммы внутренних углов треугольников

• Применить формулу суммы внутренних углов любого треугольника

• Вычислить недостающее измерение любого внутреннего угла любого треугольника

  900 34

Репетиторы

  180° . Вы также можете продемонстрировать доказательство суммы внутренних углов треугольников и применить формулу a + b + c = 180° , где a , b и c  – внутренние углы треугольника. Кроме того, вы можете вычислить недостающее измерение любого внутреннего угла любого треугольника, используя два разных метода.

Как найти угол в прямоугольном треугольнике

Все ресурсы по базовой геометрии

9 Диагностические тесты
164 практических теста
Вопрос дня
Карточки
Learn by Concept

← Предыдущая 1 2 3 Следующая →

Справка по базовой геометрии »
Плоская геометрия »
Треугольники »
Прямоугольные треугольники »
Как найти угол в прямоугольном треугольнике

Найти угол C.

Возможные ответы:

C=72

C=65

C=70

Ни один из этих 900 03

C=53

Правильный ответ:

C =65

Пояснение:

Во-первых, знайте, что сумма всех углов треугольника равна 180 градусам.

У каждого треугольника 3 угла. Таким образом, у нас есть сумма трех углов, как показано на рисунке:

, где у нас есть углы A, B и C. В нашем прямоугольном треугольнике один угол равен 25 градусам, и мы назовем этот угол A. Другой известный угол 90 градусов, и мы назовем этот угол B. Таким образом, у нас есть

Упростите и решите для C.

Сообщить об ошибке

Какое из следующих

может быть двумя мерами угла прямоугольного треугольника?

Возможные ответы:

Правильный ответ:

Пояснение:

В прямоугольном треугольнике не может быть тупого угла; это исключает выбор между 100 и 10.

Острые углы прямоугольного треугольника должны составлять 90 градусов. По этому критерию можно исключить три варианта:

Оставшийся вариант правильный:

Сообщить об ошибке

Угол прямоугольного треугольника в 15 раз больше, чем у другого. Чему равен меньший угол?

Возможные ответы:

Правильный ответ:

Объяснение:

Сумма углов треугольника равна 180. В прямоугольном треугольнике один угол равен 90.  Таким образом, сумма двух других углов будет равна 90.

Пусть = первый угол и = второй угол

Таким образом, уравнение для решения становится или

Таким образом, первый угол равен, а второй угол равен .

Таким образом, меньший угол равен

Сообщить об ошибке

Угол  в треугольнике, показанном ниже (не в масштабе), равен 35 градусам. Что такое угол?

Возможные ответы:

 градусы

 градусы

 градусы

 градусы

Правильный ответ:

 градусы

Пояснение:

Сумма внутренних углов треугольника всегда равна 180 градусам. Нам дан угол  и, поскольку указано, что это прямоугольный треугольник, мы знаем, что угол   равен 90 градусам. Таким образом, мы знаем 2 из 3 и можем определить третий угол.

Угол равен 55 градусам.

Сообщить об ошибке

Что из следующего не может ли быть верным для прямоугольного треугольника?

Возможные ответы:

Прямоугольный треугольник может быть равносторонним.

Меры углов прямоугольного треугольника могут суммироваться.

Один катет может быть длиннее гипотенузы.

Прямоугольный треугольник может иметь тупой угол.

Ни одно из других утверждений не может быть верным для прямоугольного треугольника.

Правильный ответ:

Ни одно из других утверждений не может быть верным для прямоугольного треугольника.

Объяснение:

Все этих утверждений ложны.

Прямоугольный треугольник может быть равносторонним.

Неверно: Равносторонний треугольник должен иметь три угла, каждый из которых измеряется.

Один катет может быть длиннее гипотенузы.

Ложь: Каждый катет на короче гипотенузы.

Прямоугольный треугольник может иметь тупой угол.

Ложь:  Оба угла прямоугольного треугольника не являются прямыми  должен быть острым.

Меры углов прямоугольного треугольника могут суммироваться.

Ложь: Меры любой суммы треугольников .

Сообщить об ошибке

Чему равен угол треугольника?

Возможные ответы:

Правильный ответ:

Объяснение:

Формула для нахождения всех углов треугольника:

Чтобы найти меру угла, мы подставляем значения и . Поскольку угол прямой, мы знаем, что мера будет равна .

Сообщить об ошибке

Найдите градусную меру недостающего угла.

Возможные ответы:

Правильный ответ:

Пояснение:

Сумма всех углов треугольника равна 180º.

Чтобы найти значение остаточного угла, вычтите известные углы из 180º:

Следовательно, третий угол равен 43º.

Сообщить об ошибке

Прямоугольный треугольник  имеет два равных угла, какова их мера?

Возможные ответы:

Правильный ответ:

Пояснение:

Сумма внутренних углов треугольника всегда равна 180 градусам, и было дано, что треугольник прямоугольный, а это означает, что один из углов равен 90 градусов.

Это оставляет 90 градусов, чтобы равномерно разделить два оставшихся угла, как было показано в вопросе.

Следовательно, каждый из двух равных углов имеет размер 45 градусов.

Сообщить об ошибке

Какого угла не хватает в этом прямоугольном треугольнике?

Возможные ответы:

Правильный ответ:

Пояснение:

Сумма углов треугольника равна .

Это означает, что .

Используя тот факт, что 90 — это половина 180, мы можем вычислить, что недостающий угол x плюс 34 прибавляются к оставшимся 90, и мы можем просто вычесть

.

Сообщить об ошибке

Решить:

Возможные ответы:

Правильный ответ:

900 02
Пояснение:

Сумма углов треугольника составляет 180 градусов.