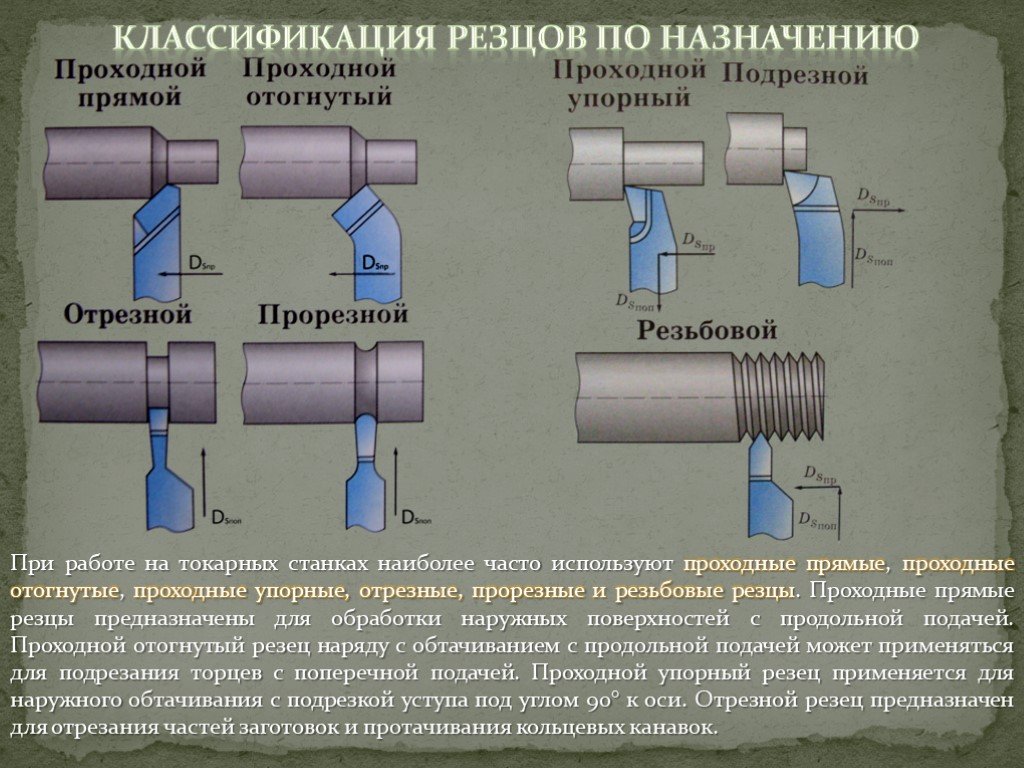
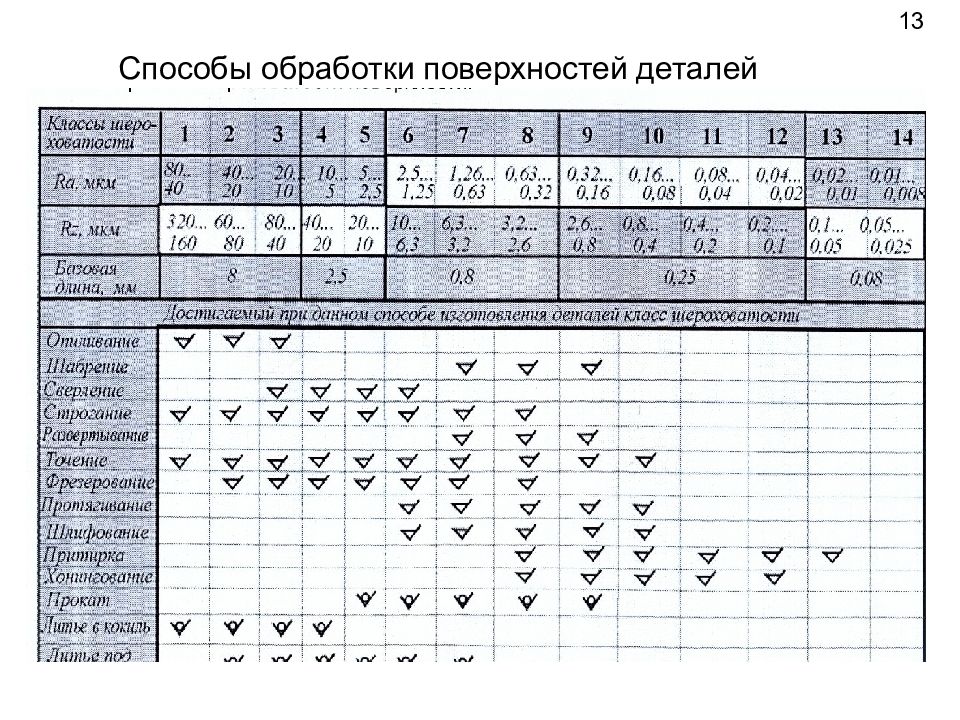
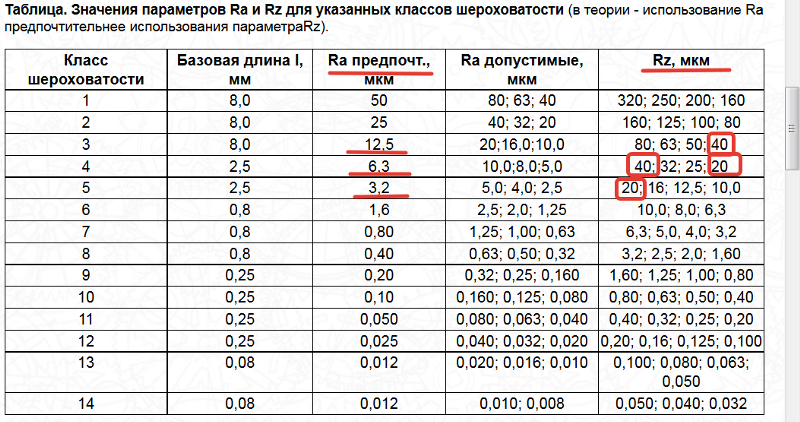
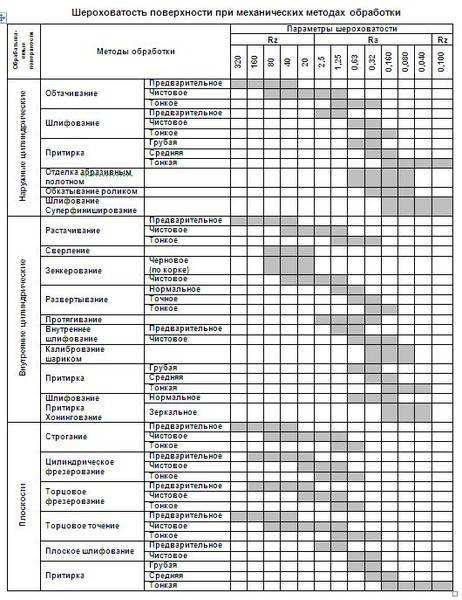
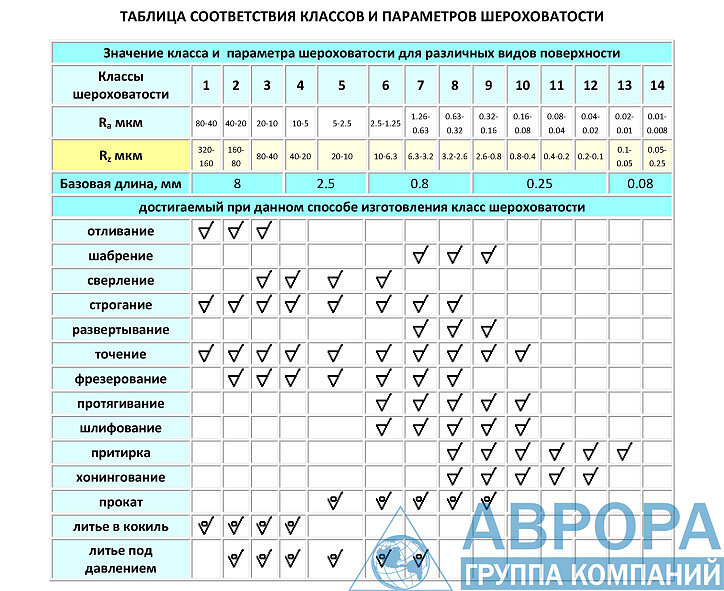
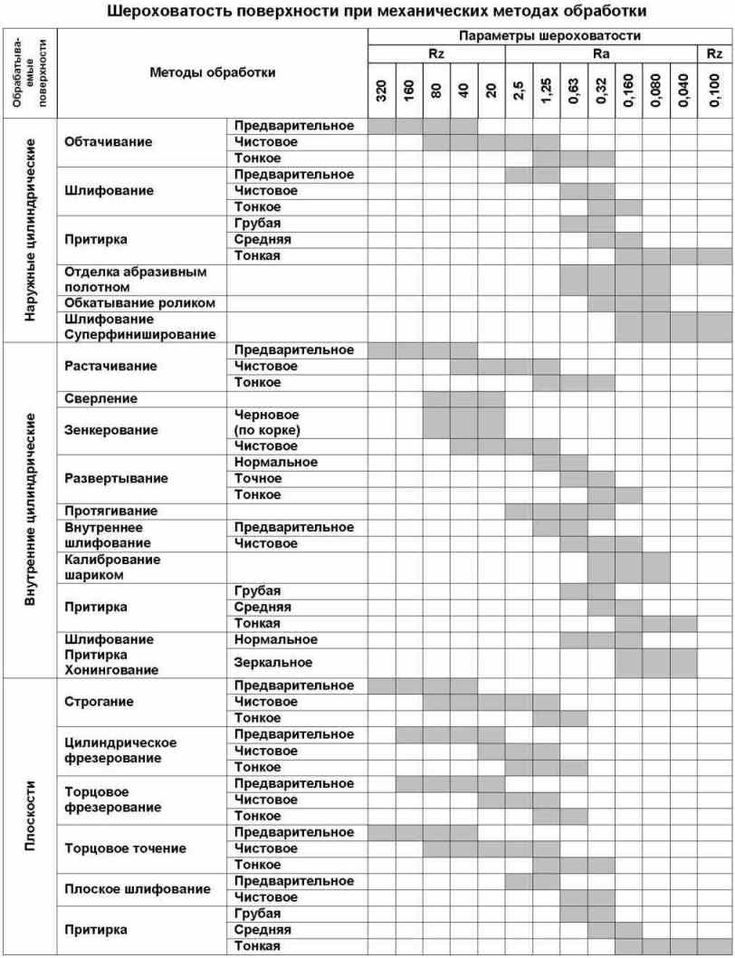
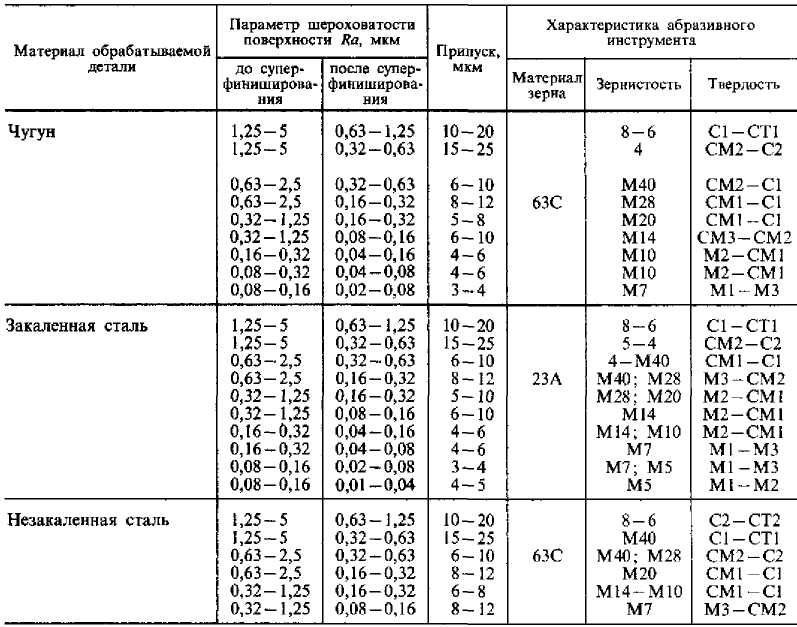
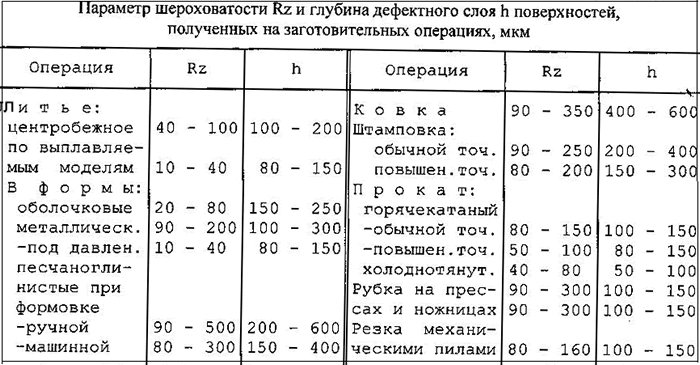
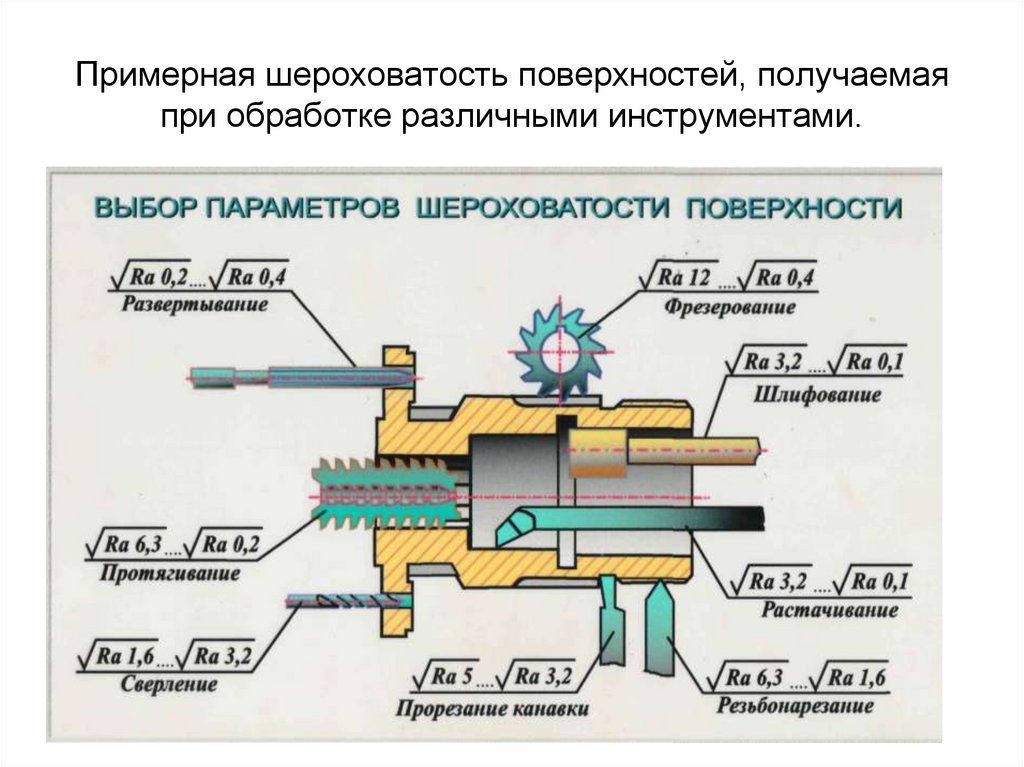
Параметры обрабатываемой поверхности: Параметры обработки, влияющие на выбор абразивного материала: качество обработки

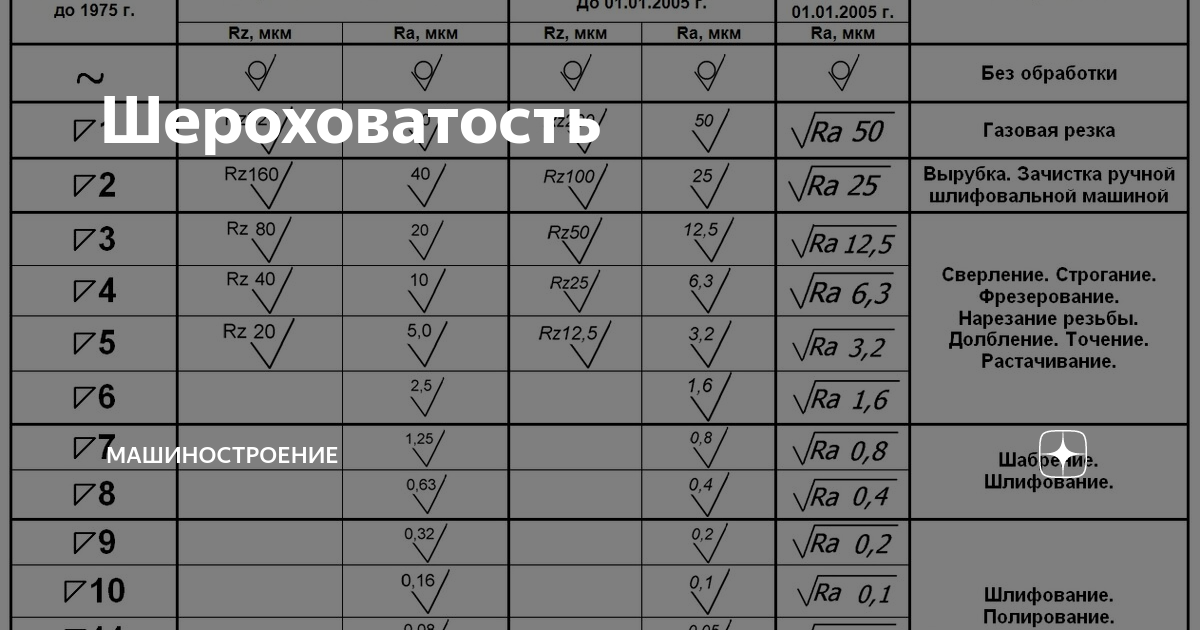
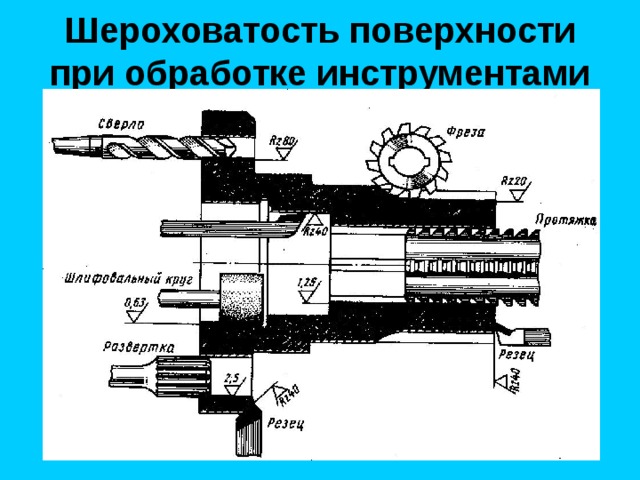
Шероховатость поверхности. Основные понятия

• Главная /
• Точность в машиностроении /
• Шероховатость поверхности

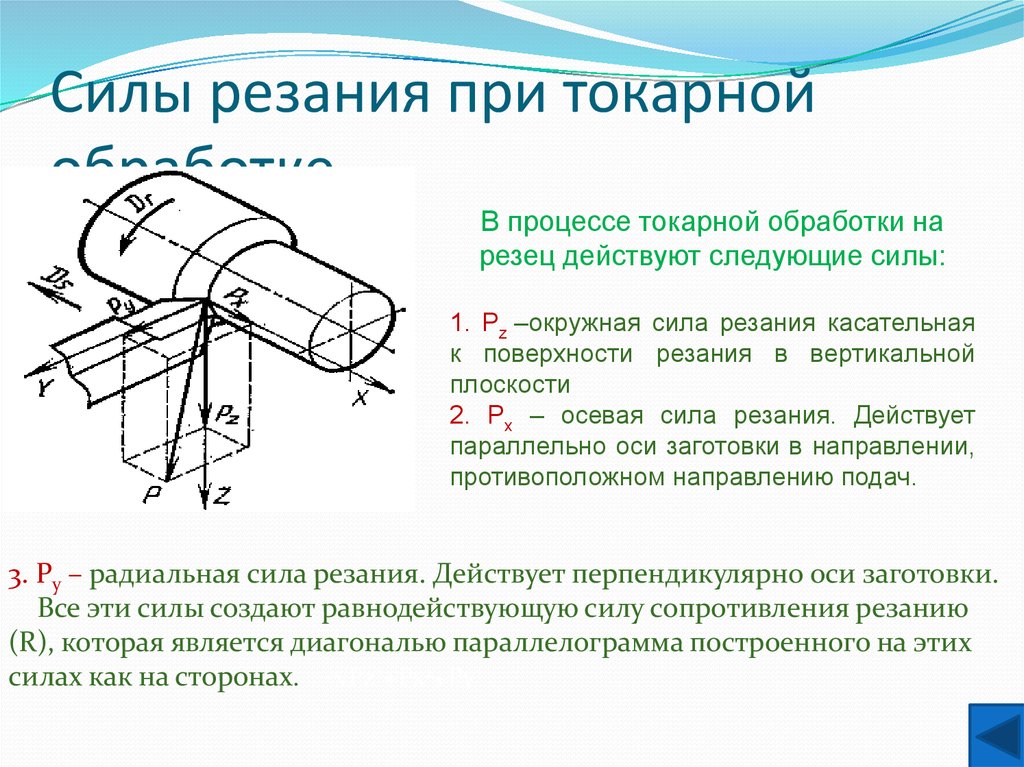
Шероховатостью поверхности называется совокупность микронеровностей, образующих рельеф поверхности и рассматриваемых в пределах участка, длина которого равна базовой длине.

В большинстве случаев шероховатость поверхности определяется одним из параметров Ra или Rz.

Высота неровностей профиля по десяти точкам Rz — является суммой средних абсолютных значений высот точек пяти наибольших выступов профиля и глубин пяти наибольших впадин в пределах базовой длины, измеренных от произвольной линии АВ

Среднее арифметическое отклонение профиля Ra – это среднее арифметическое абсолютных значений отклонений профиля yi от
средней линии m в пределах базовой длины

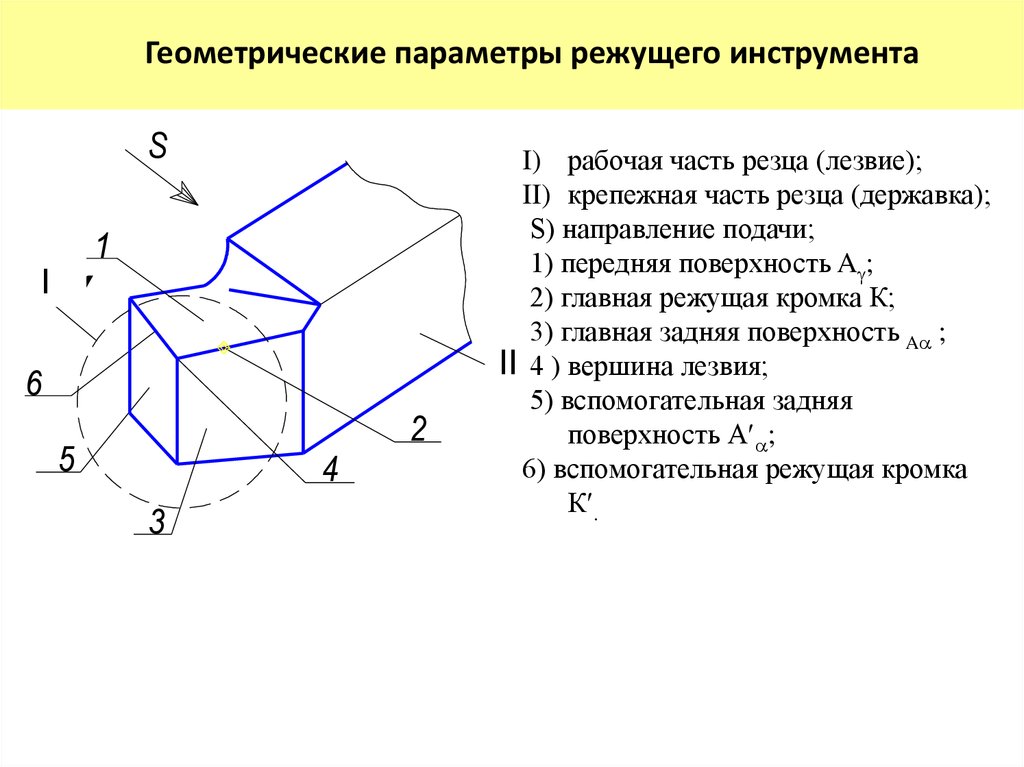
Рисунок 1.

Механизм возникновения шероховатости

Все причины возникновения шероховатости можно разбить на 3 группы:

1. Расположение режущих кромок инструмента, относительно обрабатываемой поверхности;
2. Упругая и пластическая деформация обрабатываемого металла;
3. Вибрации в технологической станочной системе.

Рисунок 2.

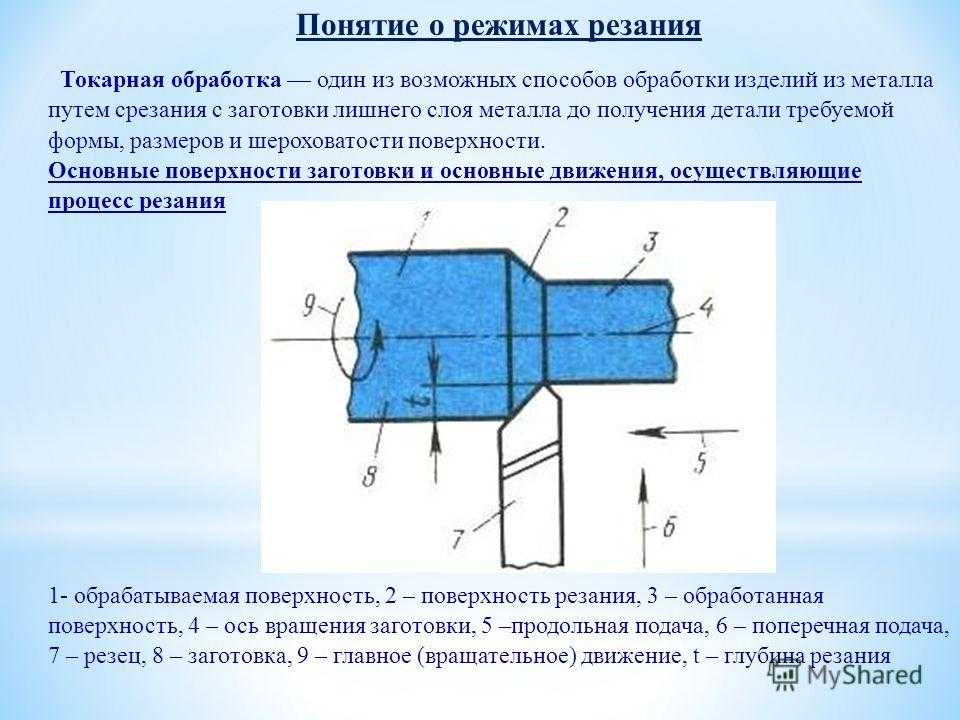
Образование неровностей на обработанной поверхности можно представить как след от движения режущих кромок инструмента.
Назовём такой профиль регулярным (рис.2).

На образование регулярного профиля влияет геометрия резца, в частности – углы в плане, а так же величина подачи S. Их
влияние описывается формулой

В реальном процессе резания впереди резца и под обработанной поверхностью образуется зона пластической деформации, которая вносит некоторую погрешность в регулярный профиль. Пластически деформированный металл в отдельных местах как бы наволакивается на микронеровности, а в где-то вырываются отдельные куски металла.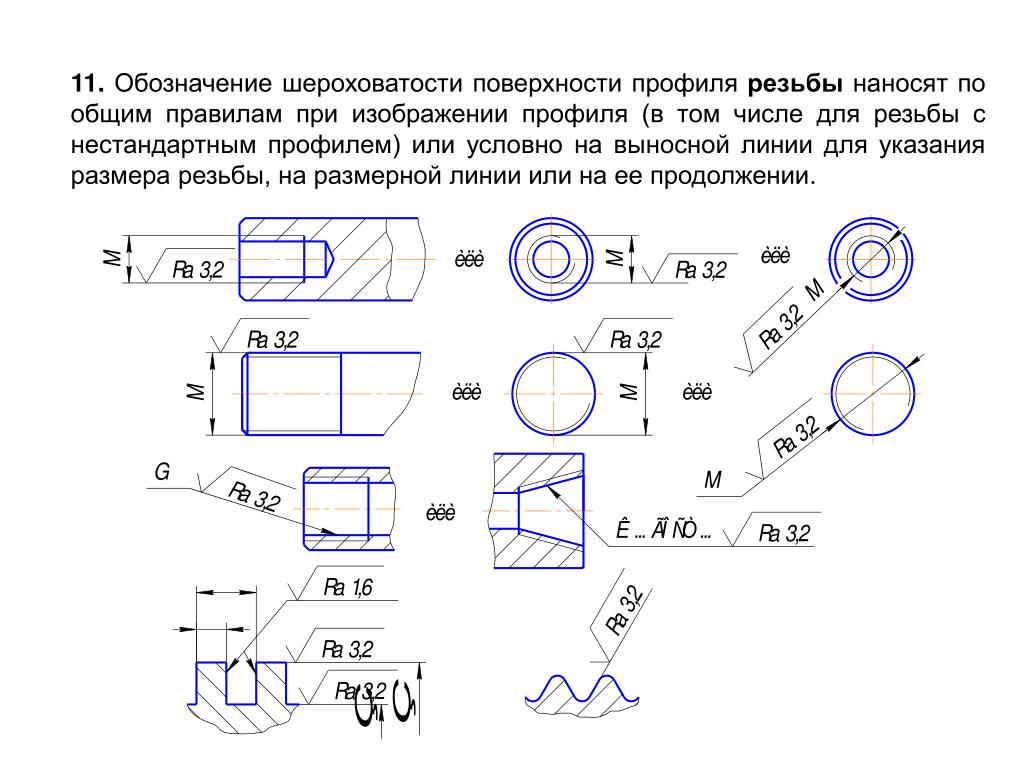 Потому реальное значение Rz может быть записано как:

где — приращение высоты микронеровностей, вызванное пластической деформацией металла.
Следовательно, чем меньше пластическая деформация, тем меньше высота микронеровностей. Величина пластической деформации зависит, в
большей степени, от твёрдости обрабатываемого материала и, в меньшей — от глубины резания — t.

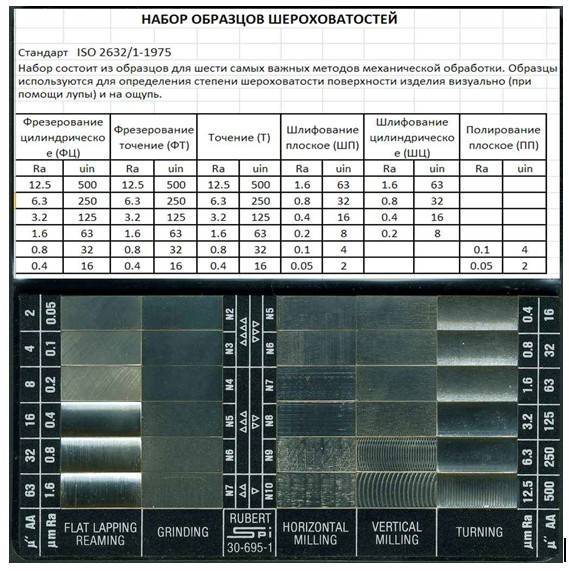
Методы и средства оценки шероховатости поверхности

Шероховатость поверхности оценивают двумя основными методами:

качественным и количественным.

Качественный метод оценки основан на визуальном сопоставлении обработанной поверхности с эталоном невооруженным глазом или под микроскопом, а также по ощущениям при ощупывании рукой (пальцем, ладонью, ногтем). Визуальным способом можно достаточно точно определять шероховатость поверхности, за исключением весьма тонко обработанных поверхностей. Эталоны, применяемые для оценки шероховатости поверхности визуальным способом, должны быть изготовлены из тех же материалов, с такой же формой поверхности и тем
же методом, что и деталь. Качественную оценку весьма тонко обработанных поверхностей следует производить с помощью микроскопа или лупы с пятикратным и большим увеличением.

Количественный метод оценки заключается в измерении микронеровностей поверхности с помощью приборов: профилографов и
профилометров.

Профилографы

Профилографы — это приборы, позволяющие получатть изображение микронеровностей профиля в увеличенном масшттабе на каком-либо носителе (фотоплёнке, фотобумаге).

Профилометры — минуя этап получения изображения, производят необходимые измерения профиля микронеровностей.

Рисунок 3.

Схема профилографа Б. М. Левина приведена на рис. 3. Луч света от лампы 1, проходя через линзу 2, щель 3 и оптическую
систему 5, падает на зеркала 8 и 7. Зеркало 8 связано с ощупывающей иглой 9. Луч света, отраженный от зеркала 7 и затем от зеркала 8, проходит оптическую систему 6 и, попадая на зеркала 4 и далее на цилиндрическую линзу 14, проецирует изображение щели 3 на
светочувствительную пленку 13,расположенную на барабане 12. Изображение щели проецируется в виде световой точки. Деталь 10, на
поверхности которой измеряют шероховатость, располагается на верхнем диске предметного стола 11. При вращении синхронного двигателя
стол вместе с деталью движется поступательно относительно иглы 9, а барабан 12 вращается. Таким образом, на светочувствительной
фотоплёнке получается изображение пути светового луча, повторяющего профиль обработанной поверхности испытуемой детали.

Принцип действия профилометра конструкции В. М. Киселева заключается в возбуждении колебаний напряжения в результате движений ощупывающей иглы. На рис. 4 приведена схема этого профилометра (модель КВ-7). Игла 1 с алмазным наконечником, радиус закругления которого 12 мкм, подвешена на пружинах 2. Нижний конец ее ощупывает неровности поверхности детали, а верхний связан с индукционной катушкой 3, которая перемещается в магнитном поле полюсов 4 и 6 магнита 5. Возбуждаемый этим перемещением ток подают на усилитель и затем на гальванометр. Перемещение иглы по поверхности осуществляют с помощью электропривода со скоростью 10…20 мм/с. Давление иглы на поверхность проверяемой детали составляет 5…25 кПа. При подключении к профилометру осциллографа можно получить профилограмму исследуемой поверхности.

Рисунок 5.

Для измерения шероховатости предназначен также двойной микроскоп В. П. Линника (рис. 5). Прибор состоит из двух частей:
микроскопа А для освещения исследуемой поверхности, микроскопа Б для наблюдения и измерения профиля поверхности. Оси обеих частей
микроскопа, наклоненные под углом 45° к исследуемой поверхности, пересекаются между собой в предметной точке объективов.

В плоскости изображения объектива 3 микроскопа А перпендикулярно плоскости оси микроскопа расположена щель 2, освещаемая
источником света 1. Объектив 3 дает уменьшенное изображение а щели 2 на проверяемой плоскости Р в виде узкой светящейся линии. При отсутствии на участке поверхности Р микронеровностей объектив 4 микроскопа Б в плоскости сетки окуляра 5 даст изображение а 2 той же узкой светящейся линии, а также изображение близлежащего участка исследуемой поверхности.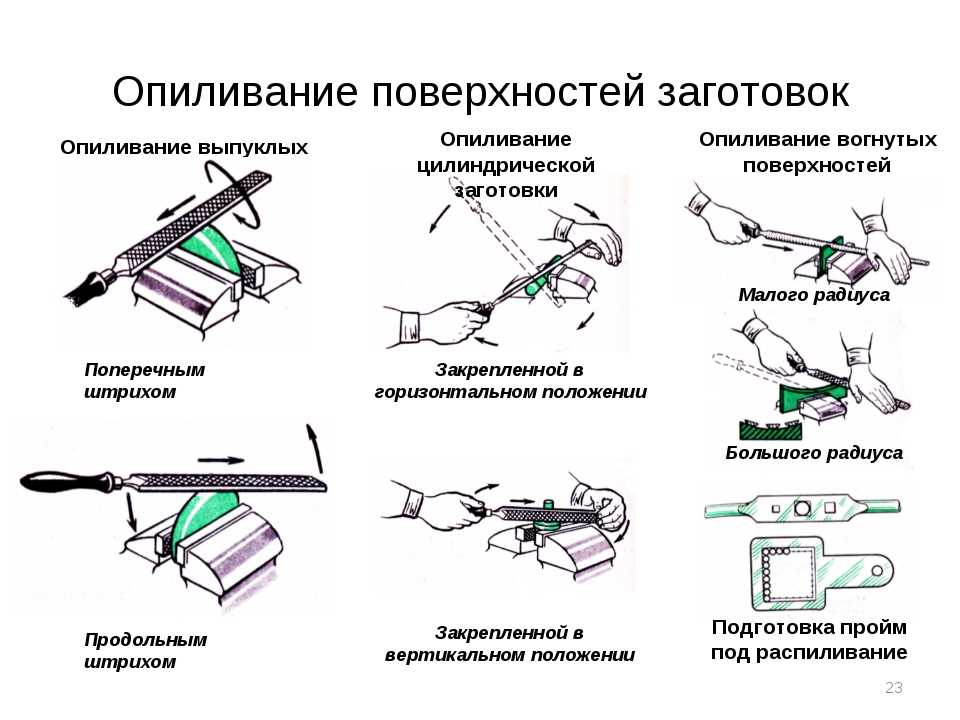

При том же расположении микроскопов А и Б при наличии микронеровностей h часть пучка света, отраженная от участка поверхности P 1 при наблюдении будет казаться выходящей из точки a 1 или из точки а 1 поверхности Р 1, расположенной на расстоянии 2h ниже поверхности Р. Тогда изображение точки из на сетке окуляра 5 будет на расстоянии h от оси микроскопа Б, равном h = 2xh sin 45°, где х — увеличение объектива 4.

Для измерений высоты неровностей в микроскопе Б установлен окулярный микрометр. Двойной микроскоп В. П. Линника позволяет также
фотографировать исследуемую поверхность с высотой неровностей 0,9…60 мкм.

• Точность обработки
• Погрешности базирования

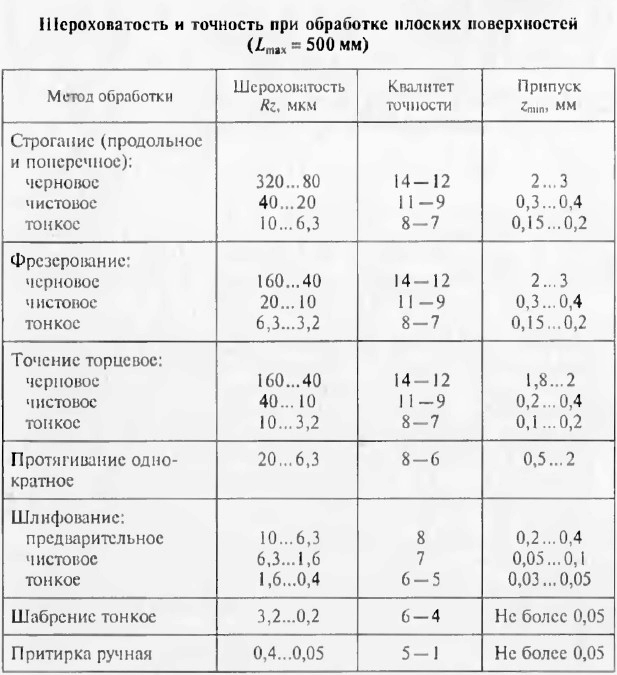
2.5.2. Факторы, влияющие на качество обработанной поверхности

Технология машиностроения / Основы технологии машиностроения / 2.5.2. Факторы, влияющие на качество обработанной поверхности

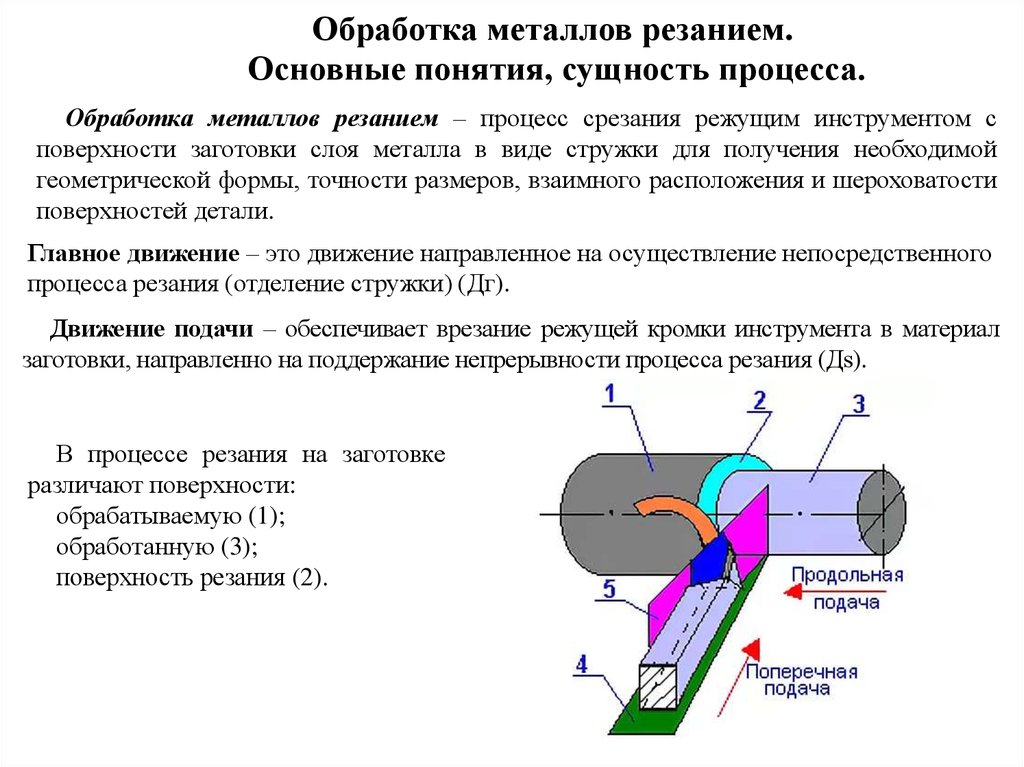
Шероховатость поверхностей деталей машин зависит от многих факторов: метода обработки, режимов резания, геометрических параметров и качества поверхностей режущей части инструмента, пластической и упругой деформации обрабатываемого материала, жёсткости технологической системы («станок – приспособление – инструмент – заготовка») и связанных с ней вынужденных деформаций, колебаний и вибраций при резании, смазочно-охлаждающей жидкости и др.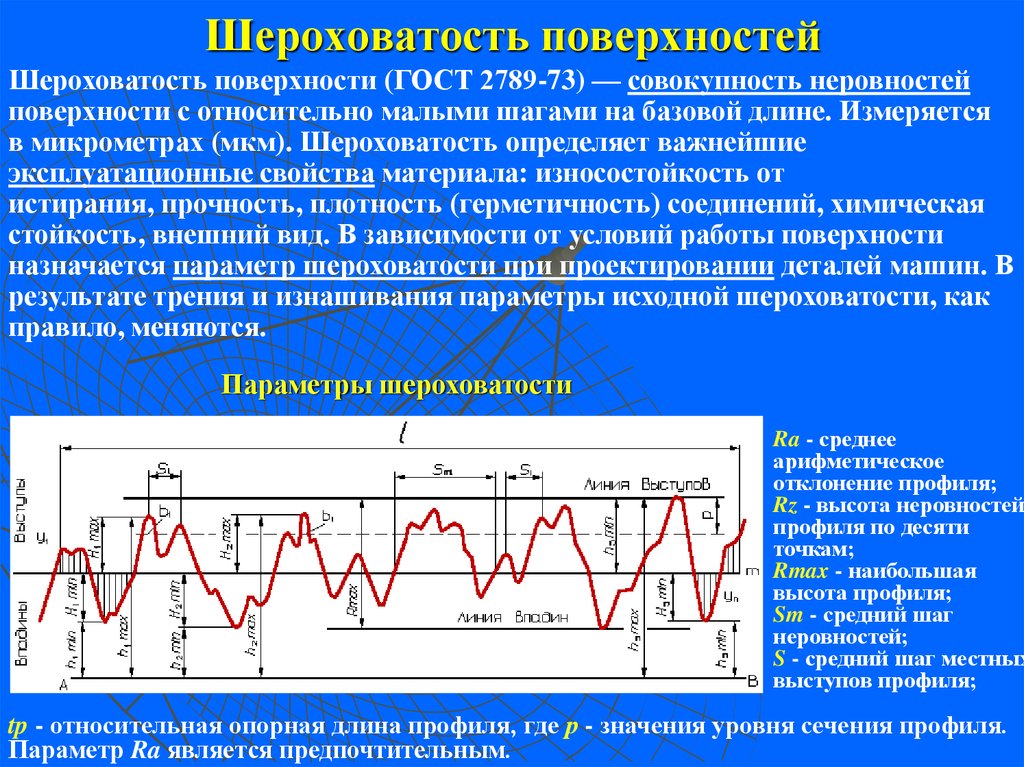

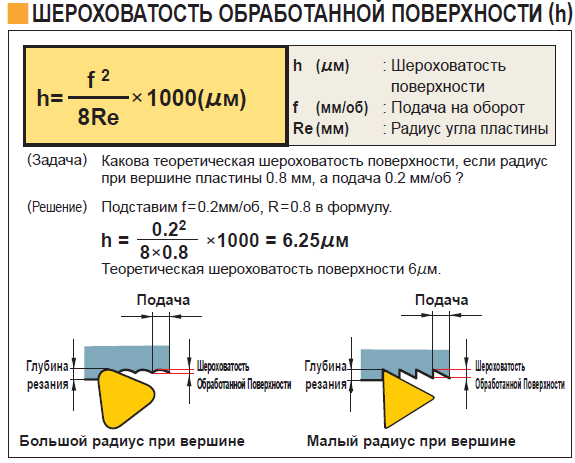
Большое влияние на шероховатость поверхности оказывает геометрия режущего инструмента, особенно при больших подачах. В этом случае шероховатость определяют в зависимости от геометрических параметров режущей части инструмента: углов в плане, главного (φ) и вспомогательного (φ₁), радиуса закругления вершины резца (r) и подачи за оборот (Sо). При увеличении r шероховатость уменьшается, сувеличением углов φ и φ₁ шероховатость поверхности увеличивается.

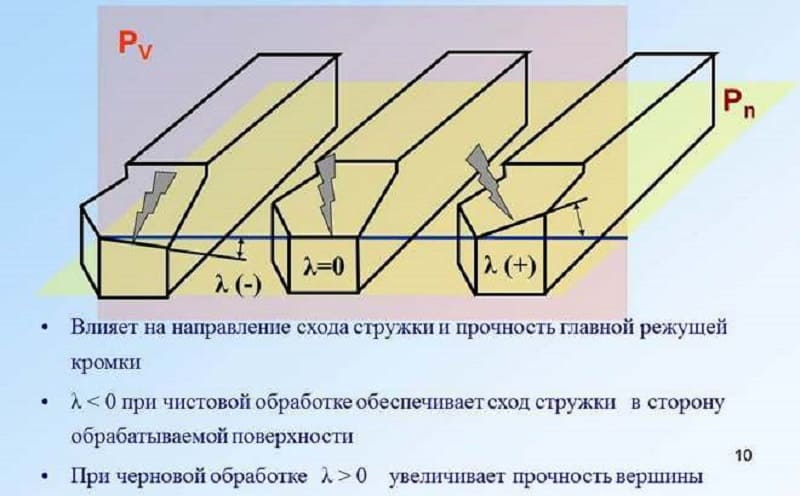
Передний угол (γ), угол наклона режущей кромки (λ), задний угол (α) могут быть отнесены к второстепенным факторам, влияющим на формирование микропрофиля.

При точении, например (рис. 2.16):

1) расчётная высота неровности поверхности (R_р) образуется закруглённым участком режущей кромки (см. рис. 2.16, а)

R_р = S₀² / 8 r,

где S₀ – подача за оборот, мм/об; r – радиус закругления резца при вершине, мм;

2) расчётная величина шероховатости Rр образуется вершиной резца, у которой отсутствует радиус закругления  (см.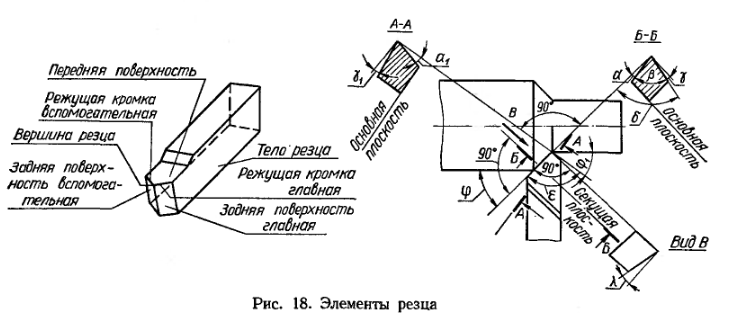 рис. 2.16, б)

R_р = S₀ Sinφ Sinφ₁ / Sin (φ + φ₁).

Значительное влияние на искажение шероховатости поверхности оказывает пластическая деформация. При обработке материалов, которые не образуют нароста, влияние пластической деформации на шероховатость объясняется главным образом распространением волны деформации в сторону соседнего следа, а при обработке материалов, образуют нарост, кроме того и действием вершины нароста, поэтому образуются задиры материала на поверхности среза.

Влияние упругих деформаций на шероховатость поверхности является следствием наличия на лезвии любого инструмента притупления. При взаимном перемещении резца и заготовки наличие этого скругления вызывает упругое деформирование материала около режущей кромки. Минуя её, материал заготовки приподнимается и занимает прежнее положение.

Обрабатываемая поверхность формируется режущим инструментом. Поэтому неровности его лезвия в определенной степени копируются на этой поверхности. Это наблюдается при поперечном и продольном точении, протягивании, цилиндрическом фрезеровании и др.

При выборе или проектировании режущего инструмента, при установлении режимов резания, выборе смазочно-охлаждающей жидкости и способа её подвода в рабочую зону необходимо стремиться к рациональному отводу стружки, чтобы исключить отрицательного воздействия на формирование обработанной поверхности.

Деформации и вибрации технологической системы увеличивают шероховатость обрабатываемой поверхности.

Из режимов резания наиболее существенное влияние на процесс образования шероховатости поверхности оказывают подача и скорость резания.

При увеличении подачи в пределах от 0,25 до 0,7 мм/об.

увеличивается почти пропорционально и шероховатость поверхности, а дальше принимает постоянное значение. При малых подачах (меньше 0,25 мм/об.) уменьшение подачи весьма незначительно уменьшает шероховатость.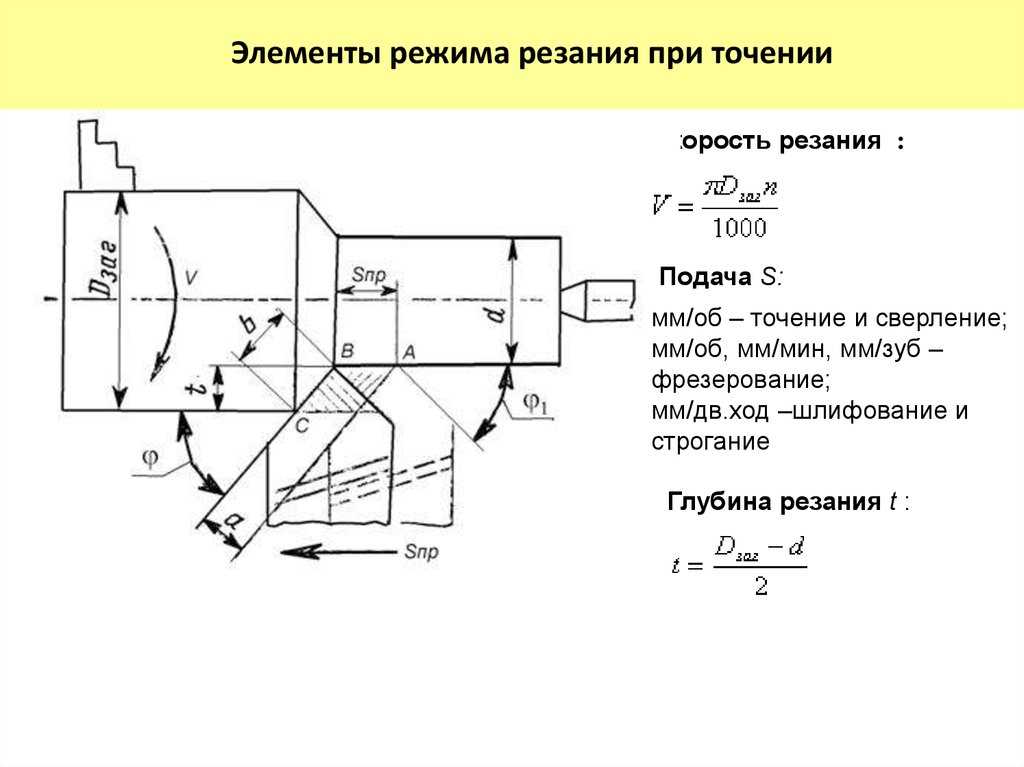

Экспериментальными исследованиями установлена связь скорости резания при обработке сталей с образованием нароста и шероховатостью обрабатываемой поверхности. Различают четыре зоны:

· первая зона соответствует малым скоростям резания (V до 1 м/мин). Она характеризуется тем, что нарост в ней отсутствует, поверхность получается без надиров;

· вторая зона соответствует скоростям резания 1 – 30 м/мин. В этой зоне появляется нарост, достигая здесь наибольшей высоты и соответственно наибольшей шероховатости;

· третья зона соответствует скоростям резания от 25 до80 м/мин; она характеризуется исчезновением нароста и уменьшением шероховатости;

· в четвёртой зоне скорость резания более 80 м/мин, она характеризуется отсутствием нароста. В этой зоне с изменением скорости шероховатость почти не изменяется.

Глубина резания оказывает незначительное влияние на шероховатость поверхности. Однако изменение глубины резания при малых её значениях (менее 0,3 мм) существенно изменяет условия срезания стружки и шероховатость возрастает.

Материал обрабатываемой заготовки также оказывает влияние на шероховатость поверхности. Например, стали с повышенным содержанием серы (автоматные стали) и стали с присадкой свинца после обработки резанием имеют меньшую шероховатость, чем углеродистая сталь.

Применение смазочно-охлаждающей жидкости способствует уменьшению шероховатости поверхности.

На основе экспериментальных данных, производственного опыта установлены параметры шероховатости поверхности в зависимости от различных методов обработки:

ü увеличение скорости резания приводит к увеличению глубины наклёпа в поверхностном слое. Однако при скоростях резания более 200 м/мин глубина наклёпа уменьшается, в результате действия высоких температур происходит разупрочнение;

ü при обработке конструкционных сталей режущим инструментом с отрицательным передним углом и при скоростях резания 500 – 800 м/мин возникают остаточные напряжения сжатия;

ü увеличение подачи приводит к возрастанию глубины наклёпа и остаточных напряжений;

ü при увеличении заднего угла (α) с 3 до 15º^{и уменьшении главного угла в плане (φ) с 90 до 45 ºглубина наклёпа уменьшается;}

ü увеличение радиуса скругления режущей кромки приводит к возрастанию глубины наклёпа и остаточных напряжений.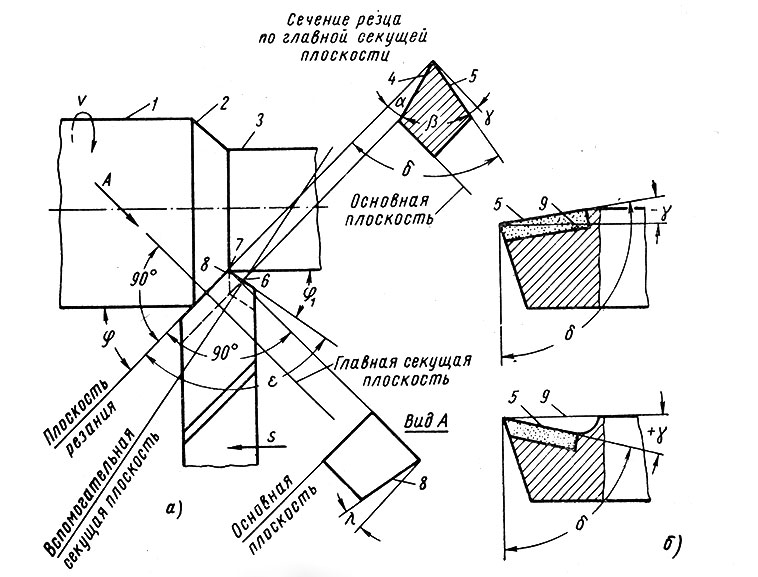

Параметры поверхности (Spatial Analyst) — ArcGIS Pro

В этом разделе

1. Сводка
2. Использование
3. Параметры
4. Среды
5. Информация о лицензировании
6. 6
7. 6
8. Параметры

   Доступно с лицензией Spatial Analyst.

   Доступно с лицензией 3D Analyst.

   Сводка

   Определяет параметры растровой поверхности, такие как экспозиция, наклон и кривизна.

   Узнайте больше о том, как работают параметры поверхности

   Использование

   • Выходные параметры рассчитываются для каждой ячейки путем подбора локальной поверхности вокруг целевой ячейки. Доступные параметры поверхности для параметра Тип параметра (parameter_type в Python): Уклон, Экспозиция, Средняя кривизна, Тангенциальная (нормальный контур) кривизна, Профиль (нормальная линия наклона) кривизны, План (проецируемый контур) кривизны, Контурное геодезическое кручение, Гауссова кривизна и кривизна Казорати.

   • Все выходные параметры рассчитываются с использованием геодезических координат и уравнений.

   • Если для параметра Тип параметра указан параметр Уклон (НАКЛОН в Python), выходные данные представляют собой скорость изменения отметки для каждой ячейки цифровой модели рельефа (ЦМР). Это первая производная ЦМР. Диапазон значений вывода наклона зависит от типа единиц измерения.

   • Если для Тип параметра указан параметр Пропорция (АСПЕКТ в Python), в выходных данных указывается направление по компасу, к которому обращен склон спуска для каждого местоположения. Он выражается в положительных градусах от 0 до 360, отсчитываемых по часовой стрелке от севера.

   • Кривизна используется для описания формы поверхности. Применительно к наукам о Земле он помогает понять влияние гравитации, эрозии и других факторов на поверхность и используется в сочетании с другими параметрами поверхности для идентификации и классификации форм рельефа.

     • Средняя кривизна (MEAN_CURVATURE в Python) — общая кривизна поверхности. Он рассчитывается как среднее значение минимальной и максимальной кривизны. Когда это указано для Типа параметра, выходные данные эквивалентны среднему значению кривизны профиля (нормальная линия наклона) и касательной (нормальный контур). Его знак, положительный или отрицательный, не является окончательным показателем, за исключением крайних значений. Высокие положительные значения указывают на области максимальной денудации, а высокие отрицательные значения указывают на области максимальной аккумуляции (Minár et al., 2020).
     • Кривизна профиля (линия нормального наклона) (PROFILE_CURVATURE в Python) — кривизна геометрического нормали вдоль линии наклона. Положительные значения указывают на области ускорения поверхностного стока и эрозии. Отрицательная кривизна профиля указывает на области замедления поверхностного течения и отложений. Положительная кривизна профиля (линия нормального наклона) указывает на то, что поверхность в этой ячейке выпукла в направлении уклона. Отрицательная кривизна указывает на то, что поверхность вогнута в этой ячейке в том же направлении. Значение 0 указывает, что поверхность плоская.
     • Тангенциальная кривизна (нормальный контур) (TANGENTIAL_CURVATURE в Python) — геометрическая нормальная кривизна, перпендикулярная линии наклона и касающаяся линии контура. Положительные значения указывают на области расходящегося поверхностного потока. Отрицательная тангенциальная кривизна указывает на области сходящегося поверхностного потока. Положительная тангенциальная (нормальный контур) кривизна указывает на то, что поверхность выпукла в этой ячейке, перпендикулярной направлению уклона. Отрицательная кривизна указывает на то, что поверхность вогнута в этой ячейке в направлении, перпендикулярном уклону. Значение 0 указывает, что поверхность плоская.
     • Кривизна плана (проецируемого контура) (CONTOUR_CURVATURE в Python) — кривизна вдоль контурных линий.
     • Contour geodesic torsion (CONTOUR_GEODESIC_TORSION в Python) — скорость изменения угла наклона вдоль изолиний.
     • Гауссова кривизна (GAUSSIAN_CURVATURE в Python) — общая кривизна поверхности. Он вычисляется как произведение минимальной и максимальной кривизны и может принимать отрицательные и положительные значения. Положительные значения указывают на то, что
       поверхность выпуклая в этой ячейке, а отрицательные значения указывают
       что он вогнутый. Значение 0 указывает, что поверхность
       плоский.
     • Кривизна Казорати (CASORATI_CURVATURE в Python) — общая кривизна поверхности. Он может быть нулевым или всегда положительным. Высокие положительные значения указывают на области резкого изгиба в нескольких направлениях.

     Единицами всех выходных данных типа кривизны будут обратные величины (квадрат обратной величины для гауссовой кривизны) x,y-единиц выходной системы координат.

   • Параметр «Квадратичный» (QUADRATIC в Python) параметра «Локальный тип поверхности» (local_surface_type в Python) не точно соответствует соседним ячейкам. Это параметр по умолчанию и рекомендуемый для большинства данных и приложений.

     • Квадратичная поверхность сводит к минимуму влияние зашумленных данных поверхности, таких как лидарная поверхность высокого разрешения, что особенно важно при вычислении кривизны.
     • Используйте квадратичную поверхность при указании размера окрестности, превышающего размер ячейки, и при использовании опции адаптивной окрестности.

   • Опция Biquadratic (BIQUADRATIC в Python) параметра типа локальной поверхности точно соответствует данным из соседних ячеек.

     • Этот вариант подходит для высокоточной поверхности ввода.
     • Если расстояние до окрестности больше, чем размер ячейки входного растра, преимущества точности биквадратного типа поверхности будут потеряны. Оставьте расстояние соседства по умолчанию (равное размеру ячейки).

   • Параметр Расстояние окрестности (neighborhood_distance в Python) определяет размер окрестности и вычисляет параметр поверхности на этом расстоянии от центра целевой ячейки.

     • Не может быть меньше размера ячейки входного растра.
     • Меньшее расстояние по соседству отражает большую локальную изменчивость ландшафта, характеристики более мелких элементов ландшафта. Для данных о высоте с высоким разрешением могут быть более подходящими большие расстояния.

   • Если установлен флажок Использовать адаптивное соседство (use_adaptive_neighborhood имеет значение ADAPTIVE_NEIGHBORHOOD в Python), расстояние соседства будет меняться в зависимости от изменчивости рельефа. Расстояние соседства будет уменьшаться, если в окне расчета слишком большая изменчивость.

   • Указание значения параметра Z-единицы поверхности (z-единицы в Python) важно для обеспечения правильного вычисления выходных данных уклона.

     Если в вертикальной системе координат входного растра доступна единица измерения z, она будет применена автоматически. Рекомендуется определить единицу измерения z для входного растра, если она отсутствует. Вы можете использовать инструмент Определить проекцию, чтобы указать z-единицу. Если он не определен, счетчик будет использоваться по умолчанию.

   • Диапазон значений в выходных данных уклона зависит от единиц измерения выходного уклона (output_slope_measurement в Python):

     • Градусов (DEGREE в Python) — диапазон значений уклона составляет от 0 до 90.
     • Рост в процентах (PERCENT_RISE в Python) — диапазон от 0 до практически бесконечности. Плоская поверхность составляет 0 процентов, поверхность под углом 45 градусов — 100 процентов, и по мере того, как поверхность становится более вертикальной, процентное увеличение становится все больше.

   • Если установлен флажок Проецировать геодезические азимуты (project_geodesic_azimuths имеет значение PROJECT_GEODESIC_AZIMUTHS в Python), выполняются следующие условия:

     • Север всегда представлен 360 градусами.
     • Азимуты будут проецироваться для исправления искажения, вызванного неконформной выходной системой координат. Эти углы можно использовать для точного определения точек вдоль самого крутого спуска.

     Проверьте параметр Проецировать геодезические азимуты, если вы используете выходные данные Параметры поверхности в качестве ввода обратного направления для параметра Ввод обратного направления или растра направления потока (in_back_direction_raster в Python) для инструмента в группе инструментов Расстояние.

   • Если установлен флажок Использовать экваториальный аспект (для проекта project_geodesic_azimuths установлено значение USE_EQUATORIAL_ASPECT в Python), аспект будет измеряться от точки вдоль экватора, чтобы скорректировать перекос направления, возникающий при приближении к полюсам. Этот параметр гарантирует, что оси север-юг и восток-запад перпендикулярны друг другу.

     Установите флажок Использовать экваториальный аспект, если местность находится вблизи северного или южного полюса.

   • Дополнительные сведения о средах геообработки, применимых к этому инструменту, см. в разделах Среды анализа и Spatial Analyst.

   • Ссылки:

     • Джеймс Д.Э., доктор медицины Томер, С.А. Портер. (2014). Трансскалярная сегментация формы рельефа на основе цифровых моделей рельефа высокого разрешения. Постер представлен на: Ежегодной конференции пользователей ESRI; июль 2014 г.; Сан-Диего, Калифорния.
     • Минар, Дж., Эванс, И.С., и Дженчо, М. (2020). Всеобъемлющая система определений кривизны земной поверхности (топографическая) с последствиями для их применения в геолого-геофизическом моделировании и прогнозировании. Earth-Science Reviews, 103414. https://doi. org/10.1016/j.earscirev.2020.103414

   Параметры

   Метка	Объяснение	Тип данных
   Входная поверхность растр	Входная поверхность.	Растровый слой
   Тип параметра (Необязательно)	Указывает тип параметра выходной поверхности, который будет вычисляться. Уклон — будет вычислена скорость изменения высоты. Это значение по умолчанию. Пропорция — будет вычислено нисходящее направление максимальной скорости изменения для каждой ячейки. Средняя кривизна — будет измерена общая кривизна поверхности. Он рассчитывается как среднее значение минимальной и максимальной кривизны. Эта кривизна описывает внутреннюю выпуклость или вогнутость поверхности, независимую от направления или влияния силы тяжести. Тангенциальная кривизна (нормальный контур) — будет измеряться геометрическая нормальная кривизна, перпендикулярная линии наклона, касательной к контурной линии. Эта кривизна обычно применяется для характеристики схождения или расхождения потока по поверхности. Кривизна профиля (нормальная линия наклона) — измеряется геометрическая нормальная кривизна вдоль линии наклона. Эта кривизна обычно применяется для характеристики ускорения и замедления потока вниз по поверхности. Кривизна плана (проекции контура) — измеряется кривизна вдоль линий контура. Контурное геодезическое кручение — будет измеряться скорость изменения угла наклона вдоль горизонталей. Гауссова кривизна — измеряется общая кривизна поверхности. Он вычисляется как произведение минимальной и максимальной кривизны. Кривизна Касорати — измеряется общая кривизна поверхности. Это может быть ноль или любое другое положительное число.	Строка
   Тип локальной поверхности (Необязательно)	Указывает тип функции поверхности, которая будет размещена вокруг целевой ячейки. Quadratic — функция квадратичной поверхности будет подогнана к соседним ячейкам. Это значение по умолчанию. Biquadratic — биквадратная функция поверхности будет подогнана к соседним ячейкам.	Строка
   Расстояние до окрестности (Необязательно)	Выходные данные будут рассчитаны для этого расстояния от центра целевой ячейки. Он определяет размер соседства. Значение по умолчанию — размер ячейки входного растра, в результате получается окрестность 3 на 3.	Линейная единица
   Использовать адаптивную окрестность (Необязательно)	Указывает, будет ли расстояние до окрестности меняться при изменении ландшафта (адаптивно). Максимальное расстояние определяется расстоянием соседства. Минимальное расстояние равно размеру ячейки входного растра. Не отмечено — во всех местоположениях будет использоваться единое (фиксированное) соседнее расстояние. Это значение по умолчанию. Флажок отмечен — во всех местоположениях будет использоваться адаптивное расстояние соседства.	Логический
   Единица Z (Необязательно)	Линейная единица вертикального z-значения. Определяется вертикальной системой координат, если она существует. Если вертикальная система координат не существует, z-единица измерения должна быть определена из списка единиц, чтобы гарантировать правильность геодезических вычислений. По умолчанию метр. Дюймы — единицей измерения будут дюймы. Фут — единицей измерения длины будут футы. Ярд — линейной единицей будут ярды. Миля США — единицей измерения будут мили. Морская миля — линейной единицей измерения будут морские мили. Миллиметр — единицей измерения длины будут миллиметры. Сантиметр — линейной единицей измерения будут сантиметры. Метр — единицей измерения будут метры. Километр — линейной единицей измерения будут километры. Дециметр — линейной единицей измерения будут дециметры.	Строка
   Измерение выходного уклона (Необязательно)	Единицы измерения (градусы или проценты), которые будут использоваться для выходного растра уклона. Этот параметр активен только в том случае, если тип параметра — «Наклон». Градус — угол наклона будет рассчитываться в градусах. Подъем в процентах — наклон склона будет рассчитываться как процент подъема, также называемый процентным уклоном.	Строка
   Геодезические азимуты проекта (Необязательно)	Указывает, будут ли проецироваться геодезические азимуты для коррекции искажения выходного угла, вызванного выходной угловой привязкой. Не отмечено — геодезические азимуты не будут проецироваться. Это значение по умолчанию. Флажок отмечен — будут проецироваться геодезические азимуты.	Логический
   Использовать экваториальный аспект (дополнительно)	Указывает, будет ли аспект измеряться от точки на экваторе или от северного полюса. Не отмечено — экспозиция будет измеряться от северного полюса. Это значение по умолчанию. Флажок отмечен — экспозиция будет измеряться от точки на экваторе.	Булево значение

   Возвращаемое значение

   Метка	Объяснение	Тип данных
   Выходной растр	Выходной растр.	Raster

    SurfaceParameters(in_raster, {parameter_type}, {local_surface_type}, {neighborhood_distance}, {use_adaptive_neighborhood}, {z_unit}, {output_slope_measurement}, {project_geodesic_azimuths}, {use_equatorial_aspect}) 

   Name	Объяснение	Тип данных
   in_raster	Входной растр поверхности.	Растровый слой
   Тип_параметра (Необязательно)	Указывает тип параметра выходной поверхности, который будет вычисляться. НАКЛОН — Будет вычислена скорость изменения высоты. Это значение по умолчанию. СООТНОШЕНИЕ — будет вычислено нисходящее направление максимальной скорости изменения для каждой ячейки. MEAN_CURVATURE — будет измерена общая кривизна поверхности. Он рассчитывается как среднее значение минимальной и максимальной кривизны. Эта кривизна описывает внутреннюю выпуклость или вогнутость поверхности, независимую от направления или влияния силы тяжести. TANGENTIAL_CURVATURE — будет измеряться геометрическая нормальная кривизна, перпендикулярная линии наклона, касательной к контурной линии. Эта кривизна обычно применяется для характеристики схождения или расхождения потока по поверхности. PROFILE_CURVATURE — будет измеряться геометрическая нормальная кривизна вдоль линии наклона. Эта кривизна обычно применяется для характеристики ускорения и замедления потока вниз по поверхности. CONTOUR_CURVATURE — будет измеряться кривизна вдоль контурных линий. CONTOUR_GEODESIC_TORSION — будет измеряться скорость изменения угла наклона вдоль горизонталей. GAUSSIAN_CURVATURE — будет измерена общая кривизна поверхности. Он вычисляется как произведение минимальной и максимальной кривизны. CASORATI_CURVATURE — будет измерена общая кривизна поверхности. Это может быть ноль или любое другое положительное число.	Строка
   local_surface_type (Необязательно)	Указывает тип функции поверхности, которая будет размещена вокруг целевой ячейки. QUADRATIC — функция квадратичной поверхности будет подогнана к соседним ячейкам. Это значение по умолчанию. BIQUADRATIC — биквадратная функция поверхности будет подогнана к соседним ячейкам.	Строка
   окрестности_расстояние (Необязательно)	Выходные данные будут рассчитаны для этого расстояния от центра целевой ячейки. Он определяет размер соседства. Значение по умолчанию — размер ячейки входного растра, в результате получается окрестность 3 на 3.	Линейная единица
   use_adaptive_neighborhood (необязательно)	Указывает, будет ли расстояние до соседства меняться при изменении ландшафта (адаптивно). Максимальное расстояние определяется расстоянием соседства. Минимальное расстояние равно размеру ячейки входного растра. FIXED_NEIGHBORHOOD — во всех местоположениях будет использоваться одно (фиксированное) расстояние соседства. Это значение по умолчанию. ADAPTIVE_NEIGHBORHOOD — во всех местоположениях будет использоваться адаптивное расстояние соседства.	Логический
   z_unit (Необязательно)	Линейная единица вертикального z-значения. Определяется вертикальной системой координат, если она существует. Если вертикальная система координат не существует, z-единица измерения должна быть определена из списка единиц, чтобы гарантировать правильность геодезических вычислений. По умолчанию метр. ДЮЙМЫ — единицей измерения будут дюймы. ФУТЫ — единицей измерения длины будут футы. ДВОР — линейной единицей измерения будут ярды. MILE_US — линейная единица измерения — мили. NAUTICAL_MILE — Линейной единицей будут морские мили. МИЛЛИМЕТР — единицей измерения длины будут миллиметры. САНТИМЕТР — линейной единицей измерения будут сантиметры. METER—Единицей измерения будут метры. КИЛОМЕТР — Линейная единица измерения — километры. ДЕЦИМЕТР — Линейной единицей измерения будут дециметры.	Строка
   output_slope_measurement (Необязательно)	Единицы измерения (градусы или проценты), которые будут использоваться для выходного растра уклона. Этот параметр доступен, только если параметр_тип = «НАКЛОН». DEGREE — угол наклона будет рассчитываться в градусах. PERCENT_RISE — наклон склона будет рассчитываться как процент подъема, также называемый процентным уклоном.	Строка
   project_geodesic_azimuths (Необязательно)	Указывает, будут ли геодезические азимуты проецироваться для коррекции искажения выходного угла. GEODESIC_AZIMUTHS — геодезические азимуты не будут проецироваться. Это значение по умолчанию. PROJECT_GEODESIC_AZIMUTHS — будут проецироваться геодезические азимуты.	Логический
   use_equatorial_aspect (Необязательно)	Указывает, будет ли аспект измеряться от точки на экваторе или от северного полюса. NORTH_POLE_ASPECT — аспект будет измеряться от северного полюса. Это значение по умолчанию. EQUATORIAL_ASPECT — аспект будет измеряться от точки на экваторе.	Булево значение

   Возвращаемое значение

   Имя	Объяснение	Тип данных
   out_raster	Выходной растр.	Растр

   Пример кода

   Пример 1 SurfaceParameters (окно Python)

   В следующем примере демонстрируется использование этого средства в окне Python.

   В этом примере создается растр уклона с выходными значениями в процентах с использованием метода адаптивного соседства. Максимальное расстояние соседства составляет 5 метров.

    из импорта arcpy.sa *
   outSurfaceParameters = SurfaceParameters("elevation_1m. tif", "", "", "5 МЕТРОВ",
                                            "ADAPTIVE_NEIGHBORHOOD", "", "PERCENT_RISE")
   outSurfaceParameters.save("C:/sapyexamples/output/outsurfaceparameters01.tif") 

   Пример 2 SurfaceParameters (автономный сценарий)

   В следующем примере демонстрируется использование этого средства в автономном скрипте Python.

   В этом примере создается растр кривизны профиля (линия нормального уклона) с использованием метода адаптивного соседства. Максимальное расстояние соседства составляет 10 метров.

    # Имя: SurfaceParameters_Ex_02.py
   # Описание: Получение кривизны профиля (линии нормального уклона) для разрешения 1 м
   # растр высот с адаптивным соседним расстоянием не более 10 м.
   # Требования: Расширение Spatial Analyst
   # Импорт системных модулей
   импортировать аркпи
   импорт из arcpy.sa *
   # Установить параметры среды
   arcpy.env.workspace = "C:/sapyexamples/data"
   # Ознакомьтесь с лицензией дополнительного модуля ArcGIS Spatial Analyst
   arcpy.CheckOutExtension("Пространственный")
   # Установить локальные переменные
   inRaster = "elevation_1m. tif"
   inParameterType = "PROFILE_CURVATURE"
   inNeighborhoodDistance = "10 МЕТРОВ"
   inUseAdaptiveNeighborhood = "ADAPTIVE_NEIGHBORHOOD"
   # Запустить инструмент
   outSurfaceParameters = SurfaceParameters(inRaster, inParameterType, "",
                                            inNeighborhoodDistance, inUseAdaptiveNeighborhood)
   # Сохраняем вывод
   outSurfaceParameters.save("C:/sapyexamples/output/outsurfaceparameters02.tif") 

   SurfaceParameters, пример 3 (автономный скрипт)

   В следующем примере демонстрируется использование этого средства в автономном скрипте Python.

   В этом примере создается растр аспекта с использованием расстояния окрестности 5 метров. Исправьте искажения направления из-за использования неконформной проекции.

    # Имя: SurfaceParameters_Ex_03.py
   # Описание: Получить экспозицию для поверхности высот на расстоянии 5 м, правильно
   # для искажения направления из-за неконформной проекционной системы.
   # Требования: Расширение Spatial Analyst
   # Импорт системных модулей
   импортировать аркпи
   импорт из arcpy. sa *
   # Установить параметры среды
   arcpy.env.workspace = "C:/sapyexamples/data"
   # Ознакомьтесь с лицензией дополнительного модуля ArcGIS Spatial Analyst
   arcpy.CheckOutExtension("Пространственный")
   # Установить локальные переменные
   inRaster = "elevation_1m.tif"
   inParameterType = "АСПЕКТ"
   inNeighborhoodDistance = "5 МЕТРОВ"
   inProjectGeodesicAzimuths = "PROJECT_GEODESIC_AZIMUTHS"
   # Запустить инструмент
   outSurfaceParameters = SurfaceParameters(inRaster, inParameterType, "",
                                            inNeighborhoodDistance, "", "", "",
                                            inProjectGeodesicAzimuths)
   # Сохраняем вывод
   outSurfaceParameters.save("C:/sapyexamples/output/outsurfaceparameters03.tif") 

   Окружающая среда

   Автоматическая фиксация, Размер ячейки, Метод проецирования размера ячейки, Текущая рабочая область, Экстент, Географические преобразования, Маска, Выходное ключевое слово CONFIG, Выходная система координат, Временная рабочая область, Растр привязки, Размер плитки

   Информация о лицензировании

   • Требуется Spatial Analyst или 3D Analyst
   • Standard: Требуется Spatial Analyst или 3D Analyst
   • Расширенный: Требуется Spatial Analyst или 3D Analyst

   Похожие темы

   ---

   Отзыв по этой теме?

   Как работают параметры поверхности — ArcGIS Pro

   Доступно с лицензией Spatial Analyst.

   Доступно с лицензией 3D Analyst.

   Инструмент Параметры поверхности определяет параметры растровой поверхности, такие как экспозиция, наклон и кривизна.

   Аспект

   Параметр Экспозиция поверхности определяет направление склона спуска. Значение каждой ячейки в выходном растре указывает направление по компасу, на которое обращена поверхность в этом месте. Он измеряется по часовой стрелке в градусах от 0 (на север) до 360 (снова на север), проходя полный круг. Плоским участкам, не имеющим направления вниз, присваивается значение -1.

   На следующих изображениях показан входной набор данных высот и выходной растр аспектов.

   Применение аспекта

   С типом параметра поверхности Экспозиция можно выполнять следующие действия:

   • Найти все северные склоны горы в рамках поиска лучших склонов для лыжных трасс.
   • Рассчитайте солнечное освещение для каждого места в регионе в рамках исследования по определению разнообразия жизни в каждом месте.
   • Найдите все южные склоны в гористой местности, чтобы определить места, где снег, вероятно, растает первым, в рамках исследования, направленного на выявление жилых районов, которые, вероятно, первыми пострадают от стока.

   Вычисление геодезического аспекта

   Геодезический аспект в местоположении представляет собой угловое направление α нисходящей поверхности по отношению к северу, измеренное на плоскости, касательной к поверхности эллипсоида (синяя плоскость на иллюстрации ниже).

   Чтобы вычислить экспозицию в каждом месте, квадратичная или биквадратичная поверхность подгоняется к соседним ячейкам с использованием метода наименьших квадратов (LSM). Нормаль поверхности рассчитывается в ячейке от этой поверхности. В том же месте вычисляется нормаль эллипсоида, перпендикулярная касательной плоскости поверхности эллипсоида.

   Поскольку касательная плоскость поверхности эллипсоида считается базовой плоскостью, нормаль к поверхности проецируется на эту плоскость. Наконец, геодезический аспект рассчитывается путем измерения угла α по часовой стрелке между севером и проекцией нормали к поверхности (см. рисунок выше).

   Наклон

   Параметр поверхности Наклон представляет собой крутизну каждой ячейки растровой поверхности. Чем меньше значение уклона, тем ровнее местность; чем выше значение уклона, тем круче местность.

   Выходной растр уклона может быть рассчитан в двух единицах измерения: в градусах или процентах (процент подъема). Рост в процентах лучше понять, если рассматривать его как рост, деленный на пробег, умноженный на 100. Рассмотрим треугольник B ниже. При угле 45 градусов подъем равен разбегу, а процент подъема равен 100 процентам. По мере приближения угла наклона к вертикали (90 градусов), как в треугольнике С, процент подъема начинает приближаться к бесконечности.

   Сравниваются значения уклона в градусах и процентах.

   Наклон чаще всего используется для набора данных высот, как показано на следующих изображениях. Более крутые склоны отображаются на выходном растре склонов более темно-коричневым цветом.

   Инструмент также можно использовать с другими типами непрерывных данных, такими как население, для выявления резких изменений стоимости.

   Расчеты геодезического уклона

   Геодезический уклон — это угол, образованный между топографической поверхностью и поверхностью эллипсоида. Любая поверхность, параллельная поверхности эллипсоида, имеет наклон, равный 0. Чтобы вычислить наклон в каждом месте, квадратичная или биквадратичная поверхность подгоняется к соседним ячейкам с использованием метода наименьших квадратов (LSM). Нормаль поверхности рассчитывается в ячейке от этой поверхности. В том же месте вычисляется нормаль эллипсоида, перпендикулярная касательной плоскости поверхности эллипсоида. Наклон в градусах вычисляется из угла между нормалью эллипсоида и нормалью топографической поверхности. Этот угол такой же, как между топографической поверхностью и поверхностью эллипсоида.

   Обзор кривизны поверхности

   Кривизна — это набор типов параметров поверхности, используемых для описания формы поверхности, обычно вдоль линии на поверхности, созданной пересечением плоскости через поверхность. Концептуально геометрическая кривизна находит наиболее подходящую окружность (соприкасающуюся окружность), чтобы аппроксимировать форму кривой в любой точке. Кривизна обратно пропорциональна радиусу этой окружности (1/r). Более прямая линия лучше всего подходит для большего круга, что приводит к меньшей кривизне, а более узкая изогнутая линия лучше всего подходит для меньшего круга, что приводит к большей кривизне (Crane, 2018).

   Кривизна профиля (линия нормального наклона)

   Параметр поверхности кривизны профиля (линия нормального наклона) измеряет геометрическую нормальную кривизну вдоль линии наклона. Иногда называемая кривизной профиля, ее можно представить как форму вертикального (профильного) поперечного сечения поверхности. Как показано ниже, вертикальная плоскость пересекает поверхность по оранжевой линии, и если ее отрезать, она будет выглядеть как профиль поперечного сечения поверхности.

   Эта плоскость определяется двумя векторами: желтая стрелка указывает направление градиента или стрелку линии наклона, а красная стрелка указывает нормаль к поверхности. Комбинация этих красных и желтых векторов определяет оранжевую плоскость и ее оранжевую линию пересечения с поверхностью. Кривизна профиля вычисляется по оранжевой линии (линия нормального наклона) на оранжевой плоскости.

   Здесь используется нормальная терминология линии наклона Minár et al (2020), чтобы свести к минимуму двусмысленность и путаницу с более ранней терминологией.

   Эта кривизна обычно применяется для характеристики ускорения и замедления потока вниз по поверхности под действием силы тяжести. При более высокой скорости вода может нести и перемещать большее количество материала; области ускорения становятся областями эрозии, а области замедления становятся областями отложений.

   На изображении ниже области сильно выпуклого профиля (линия нормального наклона) кривизны вокруг гребня конуса показаны фиолетовым цветом. Области сильно вогнутого профиля (линия нормального наклона) кривизны в основании конуса показаны оранжевым цветом. Области с малыми значениями кривизны прозрачны.

   Кривизна профиля (линия нормального наклона), рассчитанная на ЦММ с разрешением 5 метров, с расстоянием соседства 35 метров (окно 15 x 15 ячеек), показаны адаптивное соседство и квадратичная подгонка поверхности.

   Результаты этой кривизны отличаются от выходных данных кривизны профиля из предыдущего инструмента Кривизна. Объяснение различий между кривизной профиля и кривизной профиля (линии наклона) приведено ниже.

   Формула расчета кривизны профиля (линии нормального уклона) выглядит следующим образом:

   Тангенциальная кривизна (нормальный контур)

   Параметр поверхности Тангенциальная кривизна (нормальный контур) измеряет геометрическую нормальную кривизну, перпендикулярную линии наклона, касательной к линии контура. Он называется тангенциальной кривизной, потому что измеряет кривизну, касательную к контурной линии. Он описывается как нормальный контур (Minár et al., 2020), потому что фиолетовая секущая плоскость, которая создает фиолетовую линию, вдоль которой вычисляется кривизна, определяется вектором синего контура и вектором нормали к красной поверхности.

   Тангенциальная кривизна (нормальный контур) обычно применяется для характеристики топографической конвергенции и дивергенции потока на поверхности.

   На изображении ниже синим цветом показаны области высокой выпуклой тангенциальной (нормальный контур) кривизны вокруг гребня конуса и гребня, обращенного к вам. Это области расходящихся потоков. Области сильно вогнутой тангенциальной (нормальный контур) кривизны внутри конуса показывают сходящийся поток красным цветом. Области с малыми значениями кривизны прозрачны.

   Тангенциальная (нормальный контур) кривизна, рассчитанная на ЦММ с разрешением 5 метров, с расстоянием соседства 35 метров (окно 15 x 15 ячеек), адаптивное соседство и квадратичная подгонка поверхности.

   Формула для расчета тангенциальной (нормальный контур) кривизны выглядит следующим образом:

   План (проекция контура) кривизны

   Параметр План (проекция контура) кривизны поверхности измеряет кривизну вдоль контурных линий. Иногда это называют кривизной контура и горизонтальной кривизной. Кривизна спроецированного контура измеряется вдоль контурной линии синего цвета, где горизонтальная плоскость пересекает поверхность.

   Формула для расчета кривизны в плане (проекция контура) выглядит следующим образом:

   Изображение ниже иллюстрирует разницу между тангенциальной (нормальный контур) кривизной, измеренной вдоль фиолетовой линии, и кривизной в плане (проекция контура), измеряется по синей контурной линии.

   Контурное геодезическое кручение

   Параметр Контурное геодезическое кручение измеряет скорость изменения угла наклона вдоль горизонталей.

   Формула для расчета геодезического кручения контура выглядит следующим образом:

   Средняя кривизна

   Параметр Средняя кривизна поверхности измеряет общую кривизну поверхности. Он рассчитывается как среднее значение минимальной и максимальной кривизны. Он также математически эквивалентен среднему значению кривизны профиля (линия нормального наклона) и тангенциальной кривизны (нормальный контур). На изображении ниже показаны секущая плоскость Профиль (линия нормального наклона) (оранжевая) и плоскость сечения Тангенциальная (нормальный контур) (фиолетовая).

   Профиль (линия нормального наклона) и тангенциальная (нормальный контур) кривизна измеряют выпуклость и вогнутость в определенном направлении; тогда как средняя кривизна описывает внутреннюю выпуклость или вогнутость поверхности, независимую от направления или влияния силы тяжести. Его знак (положительный или отрицательный) не является окончательным показателем выпуклости или вогнутости, за исключением крайних значений, поскольку поверхность может быть вогнутой в одном направлении и выпуклой в другом. Высокие положительные значения указывают на области максимальной денудации, а высокие отрицательные значения указывают на области максимальной аккумуляции (Minár et al. , 2020).

   Формула для расчета средней кривизны выглядит следующим образом:

   • Где:

     K _M = Средняя кривизна

     z = f(x,y)

   Гауссова кривизна

   Параметр Гауссовой кривизны измеряет общую кривизну поверхности. Он вычисляется как произведение минимальной и максимальной кривизны и может принимать отрицательные и положительные значения. Положительные значения указывают на то, что поверхность в этой ячейке выпуклая, а отрицательные значения указывают на то, что она вогнутая. Значение 0 указывает, что поверхность плоская.

   Формула для расчета кривизны Гаусса выглядит следующим образом:

   Кривизна Касорати

   Параметр поверхности кривизны Касорати измеряет общую кривизну поверхности. Это может быть ноль или любое другое положительное число. Высокие положительные значения указывают на области резкого изгиба в нескольких направлениях.

   Формула для расчета кривизны Казорати выглядит следующим образом:

   Базовые и комбинаторные типы кривизны

   Тангенциальная кривизна (нормальный контур), кривизна профиля (линия нормального наклона) и контурное геодезическое кручение считаются основными типами кривизны, поскольку другие кривизны может быть выражена как их комбинация. Приняв терминологию Minár et al (2020), они описываются как основное трио.

   В дополнение к приведенным выше выражениям для средней кривизны, гауссовой кривизны и кривизны Казорати, эти кривизны также могут быть вычислены как комбинация базовой тройки.

   Формула для расчета средней кривизны выглядит следующим образом:

   Формула для расчета гауссовой кривизны выглядит следующим образом:

   • Где:

     K _G = Гауссова кривизна

     K _T = Тангенциальная кривизна (нормальный контур)

     K _P = кривизна профиля (линия нормального уклона)

     τ = геодезическое кручение контура

     z = f(x,y)

   к устаревшим алгоритмам инструмента Кривизна

   Инструмент Параметры поверхности использует другие алгоритмы кривизны, чем инструмент Кривизна, а также геодезическую математику в своих расчетах; поэтому не следует проводить прямое сравнение результатов этих двух инструментов. Типы кривизны Surface Parameters, Profile (нормальная линия наклона) и Tangential (нормальный контур), являются истинными геометрическими кривизнами (Minár et al. 2020). Средняя кривизна инструмента «Параметры поверхности» представляет собой среднее значение минимальной и максимальной кривизны в этой точке. Типы Profile и Planform инструмента Curvature являются производными по направлению, фактически не измеряя геометрическую кривизну поверхности в определенном месте (Zevenbergen and Thorne 19).87). Знак (положительный или отрицательный) для профиля (линия нормального уклона) в инструменте «Параметры поверхности» противоположен кривизне профиля инструмента «Кривизна». Инструмент «Параметры поверхности» выполняет вычисления в геодезическом пространстве, а инструмент «Кривизна» использует плоские координаты и математические вычисления. Инструмент «Параметры поверхности» может соответствовать квадратичной или биквадратной поверхности, инструмент «Кривизна» поддерживает только биквадратную поверхность.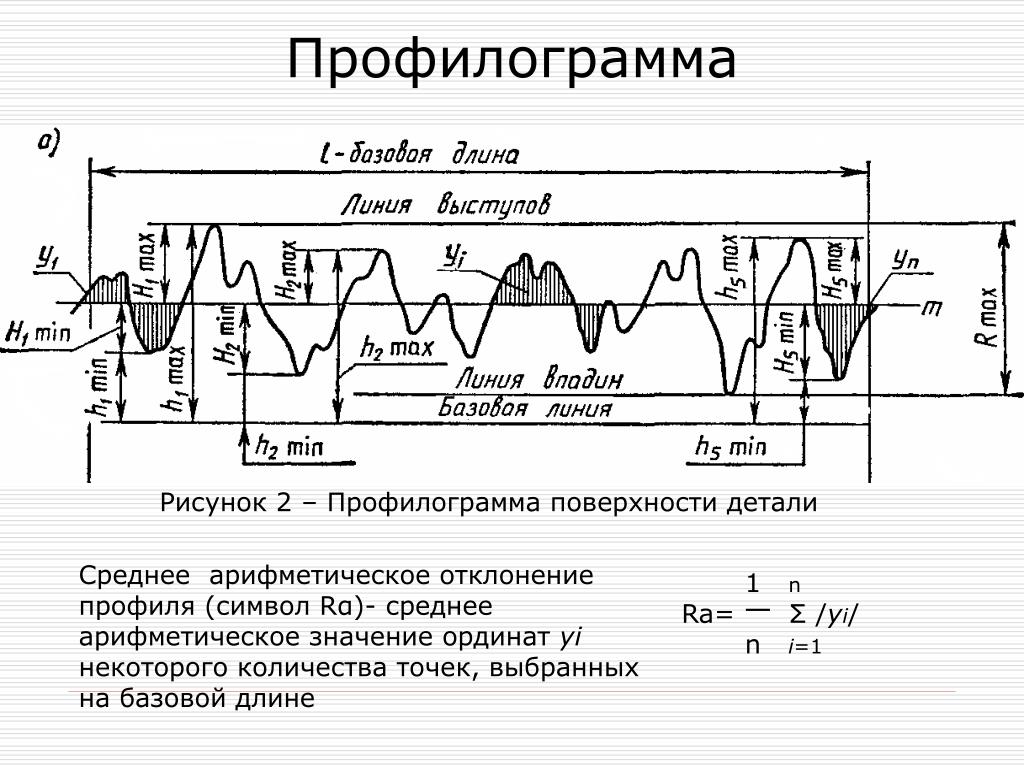

   Расстояние соседства

   Значение расстояния соседства — это расстояние карты от центра текущей обрабатываемой ячейки до центра ортогонального соседа. Меньшее соседнее расстояние фиксирует большую локальную изменчивость ландшафта, что дает характеристики более мелких элементов ландшафта. Для данных высот с более высоким разрешением более подходящим может быть большее расстояние соседства из-за ошибки мелкого масштаба (шума) в данных, которые не отражают интересующие процессы формы рельефа, или из-за того, что интересующая форма рельефа лучше распознается на больших расстояниях.

   В приведенном ниже примере используется цифровая модель поверхности (DSM) с разрешением 5 метров, которая имеет заметный шум и артефакты полос, отображаемые в результате кривизны профиля (линии нормального уклона). В первом изображении использовалось окно по умолчанию 3 x 3 или соседнее расстояние 5 метров, второе изображение представляет собой окно 9 x 9 ячеек или соседнее расстояние 20 метров, а третье изображение использовало окно 15 x 15 ячеек или соседнее расстояние 35 метров. В этом примере с увеличением расстояния до соседей наиболее значимые или основные особенности ландшафта становятся более четкими, а артефакты шума и полос становятся менее заметными. Хотя большее соседнее расстояние всегда приводит к меньшему шуму, наиболее подходящее расстояние будет зависеть от размера ячейки данных и размера элементов рельефа, важных для приложения.

   Профиль (линия нормального наклона) показана кривизна вулканического конуса на трех окрестных расстояниях. Фиолетовые области — это высокая выпуклая кривизна, а оранжевые области — высокая вогнутая кривизна.

   Наименьшее расстояние окрестности равно размеру ячейки входного растра. Наибольшее расстояние соседства равно семикратному размеру ячейки, в результате чего получается окно размером 15 x 15 ячеек. Любое указанное расстояние, превышающее размер ячейки более чем в семь раз, всегда приводит к использованию окна ячейки размером 15 x 15.

   Показана зависимость между расстоянием соседства (оранжевая линия) и числом в пикселях движущегося окна. Для размера ячейки 10 метров расстояние соседства 10 метров будет использовать окно ячейки 3 x 3 (это значение по умолчанию), расстояние соседства 20 метров будет использовать окно ячейки 5 x 5, а расстояние соседства 30 метров будет использоваться окно 7 x 7 ячеек.

   Если задано соседнее расстояние,
   не приведет к нечетному интервалу размера ячейки, он будет округлен до
   следующий интервал размера ячейки. Например, в
   приведенном выше рисунке, если бы соседнее расстояние 25 метров было
   указано, он будет округлен до следующего интервала размера ячейки,
   30 метров (в три раза больше размера ячейки), в результате получается ячейка 7 x 7
   окно.

   Если данные высот имеют гораздо более высокое пространственное разрешение, чем это необходимо для анализа интересующих форм рельефа, альтернативой варианту окна соседства является повторная выборка или агрегирование данных до большего размера ячейки, который больше подходит для приложения.

   Расчет параметров поверхности зависит от размера ячейки и расстояния до соседней области. Wilson (2018) и Minár et al (2020) представляют эффективные и актуальные сводки многочисленных исследований по этой теме.

   Адаптивная окрестность

   Если этот параметр установлен, параметр Использовать адаптивное соседство изменяет расстояние соседства (размер окна или площадь), используемое для вычисления параметра поверхности, чтобы лучше фиксировать соответствующие изменения ландшафта. Инструмент автоматически определяет подходящий размер окна, вычисляя локальное отклонение от средней высоты (DEV) (Wilson and Gallant, 2000) на основе значений всех ячеек в окрестности. Он пытается использовать максимально возможный размер окна, сводя к минимуму изменчивость поверхности (James et al., 2014). Максимальный размер используемого окна указывается в параметре Расстояние до соседства.

   При вычислении параметра поверхности с фиксированной окрестностью используются все значения ячеек в пределах окрестности. При вычислении параметра поверхности с адаптивной окрестностью используются только девять ячеек (внешние ортогональные и диагональные ячейки и центральная обрабатывающая ячейка) окрестности.

   Точки обозначают центры ячеек, используемые при расчете параметра поверхности с окном 7 x 7 при использовании адаптивного соседства.

   Адаптивное соседство особенно полезно при анализе ландшафта с элементами рельефа самого разного размера, такими как большие холмы с небольшими оврагами или руслами ручьев, из ЦМР высокого разрешения. В такой ситуации небольшое соседнее расстояние, такое как 1 метр, может использоваться для оврагов ручьев, а большее соседнее расстояние 10 или 15 метров используется для холмов.

   На приведенном ниже рисунке меньшая окрестность соответствует ручью и краю обрыва, большая окрестность соответствует переходу от холма к равнине и еще большая окрестность — почти ровному однородному плато.

   Краевой эффект расстояния соседства

   Ячейкам вокруг внешнего края выходных данных будет присвоено значение NoData, если для расчета недостаточно информации.

   При использовании опции адаптивного соседства экстент выходного растра будет уменьшаться вокруг его внешнего края на одну ячейку.

   При использовании фиксированного расстояния соседства, превышающего размер входной ячейки, экстент выходного растра будет уменьшен в соответствии с используемым расстоянием соседства. Величина уменьшения может быть рассчитана как (ширина окна в пикселях — 1) / 2

   Например, если расстояние соседства приводит к использованию окна размером 7 x 7 ячеек, выходной растр уменьшится по внешнему краю на три ячейки. .

   Квадратичная и биквадратная

   Существует два типа локальных поверхностей, которые можно подогнать к окну соседства: квадратичная и биквадратная. Значение по умолчанию квадратичное и рекомендуется для большинства данных и приложений.

   Квадратичная поверхность представляет собой аппроксимацию точек методом наименьших квадратов и не проходит точно через все точки. Не проходя точно через все точки, использование квадратичной поверхности сводит к минимуму влияние зашумленных данных о поверхности, таких как лидарная поверхность с высоким разрешением. Это дает более репрезентативный результат для всех параметров поверхности и особенно важно при вычислении кривизны.

   Квадратичная поверхность должна использоваться при указании размера окрестности, превышающего размер ячейки, и при использовании опции адаптивной окрестности.

   Биквадратная поверхность точно соответствует данным из соседних ячеек. Этот вариант подходит для высокоточной входной поверхности без случайных шумов. Если расстояние соседства больше, чем размер ячейки входного растра, преимущества точности биквадратичного типа поверхности будут потеряны; поэтому расстояние соседства следует оставить по умолчанию (равное размеру ячейки).

   Преобразование геодезических координат

   Инструмент «Параметры поверхности» выполняет расчеты в геоцентрической трехмерной системе координат, также называемой системой координат «Земля по центру, фиксация Земли» (ECEF), рассматривая форму Земли как эллипсоид. Результат вычислений не зависит от того, как проецируется набор данных. Он будет использовать z-единицы входного растра, если они определены в пространственной привязке. Если пространственная привязка входных данных не определяет z-единицы, вам нужно будет сделать это с параметром z-unit.

   Система координат ECEF представляет собой трехмерную правостороннюю декартову систему координат с центром Земли в качестве начала координат, где любое местоположение представлено координатами X, Y и Z. На следующем рисунке показан пример целевого местоположения T, выраженного в геоцентрических координатах:

   Растр поверхности преобразуется из входной системы координат в трехмерную геоцентрическую систему координат.

   Геодезические вычисления используют координаты X, Y, Z, которые рассчитываются на основе его геодезических координат (широта φ, долгота λ, высота h). Если система координат входного растра поверхности является системой координат проекции (PCS), растр сначала перепроецируется в географическую систему координат (GCS), где каждое местоположение имеет геодезическую координату. Затем он преобразуется в систему координат ECEF. Высота h (значение z) представляет собой высоту эллипсоида относительно поверхности эллипсоида. См. иллюстрацию ниже.

   Для преобразования геодезических координат (широта φ, долгота λ, высота h) в координаты ECEF используйте следующие формулы: φ) * cos(λ)

     Y  = (  N  (φ) +  h  ) * cos(φ) * sin(λ) 

     Z  = (  b 4  2 25 5 a   2  *  N  (φ) +  h  ) * sin(φ) 

   • Где:

        N  (φ) =   a    2   / √(   a    2   * cos(φ)  2   +   b    2   * sin(φ)  2  ) 

     φ = Latitude

     λ = долгота

     H = высота эллипсоидов

     A = Основная ось эллипсоида

     B = Незначительная ось ellipsoid

   66666666666666666666666666666666666666666666666666666666666 6. B = незначительная ось. выше формулы. Если единица Z входного растра указана в любой другой единице, она будет преобразована в метры.

   Рекомендуемая литература

   Для лучшего понимания методов анализа поверхности и их применения см. ссылки ниже. Кроме того, Hengl and Reuter (2008) и Wilson (2018) предоставляют исчерпывающую каталогизацию этих и многих других методов анализа местности и их приложений. Minár et al (2020) представляет исчерпывающий обзор и сравнение предыдущих работ по кривизне земной поверхности с ясностью и определением многих типов кривизны.

   Каталожные номера

   Б. Хофманн-Велленхоф, Х. Лихтенеггер и Дж. Коллинз, 2001 г. GPS — теория и практика. Раздел 10.2.1. п. 282.

   Берроу, П. А., и Макдонелл, Р. А., 1998. Принципы географических информационных систем (Oxford University Press, Нью-Йорк), 190 стр.

   Крейн К., 2018. Дискретная дифференциальная геометрия: прикладное введение. Уведомления AMS, Связь. https://www.cs. cmu.edu/~kmcrane/Projects/DDG/paper.pdf

   Дэвид Эберли, 1999. Подгонка данных методом наименьших квадратов (Geometric Tools, LLC), стр. 3.

   E.J.Krakiwsky, and D.E.Wells, 1971. Системы координат в геодезии (GEODESY AND GEOMATICS ENGINEERING, UNB), ПРИМЕЧАНИЯ К ЛЕКЦИЯМ, No16, 1971, стр. 18-38

   Hengl T. and Reuter H. 9104. Концепции геоморфометрии, программное обеспечение, приложения. Эльзевир.

   Джеймс Д.Э., доктор медицины Томер, С.А. Портер. 2014. Трансскалярная сегментация рельефа на основе цифровых моделей рельефа высокого разрешения. Постер представлен на: Ежегодной конференции пользователей ESRI; июль 2014 г.; Сан-Диего, Калифорния.

   Ланкастер, П. и Шалкаускас, К. Подгонка кривых и поверхностей: введение. London: Academic Press, 1986.

   Marcin Ligas, and Piotr Banasik, 2011. Преобразование декартовых и геодезических координат на вращающемся эллипсоиде путем решения системы нелинейных уравнений (ГЕОДЕЗИЯ И КАРТОГРАФИЯ), Vol.