Система координат c: ДЕКАРТОВА СИСТЕМА КООРДИНАТ • Большая российская энциклопедия

ДЕКАРТОВА СИСТЕМА КООРДИНАТ • Большая российская энциклопедия

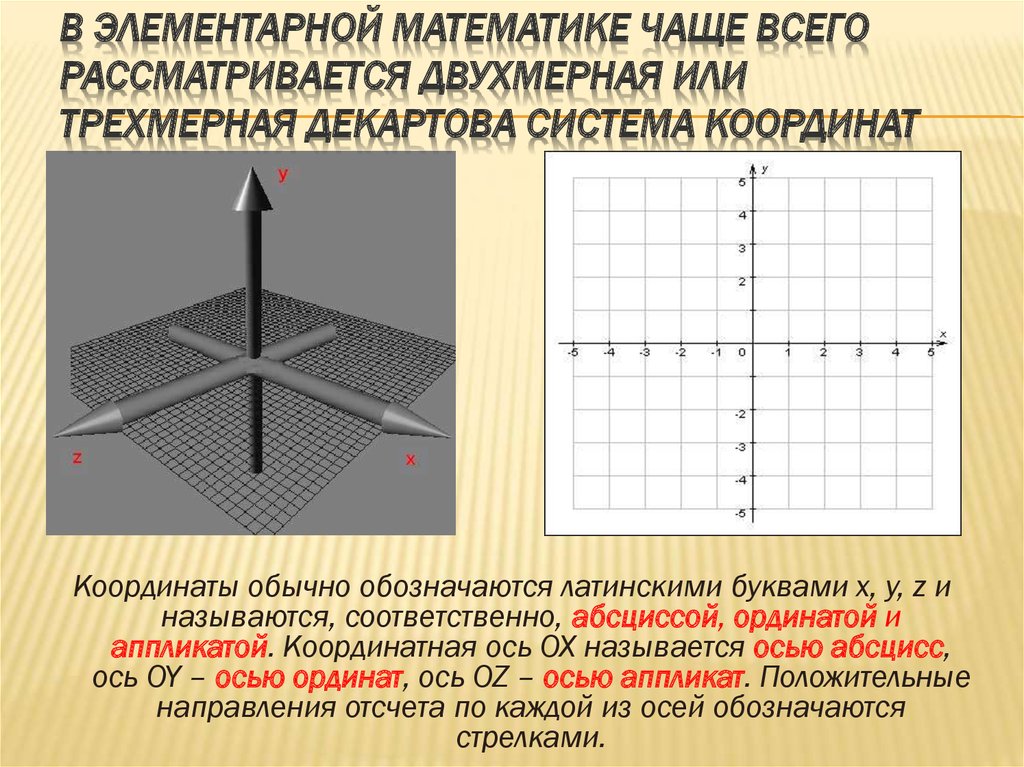
ДЕКА́РТОВА СИСТЕ́МА КООРДИНА́Т, пря­мо­ли­ней­ная сис­те­ма ко­ор­ди­нат на плос­ко­сти или в про­стран­ст­ве, в ко­то­рой по­ло­же­ние точ­ки мо­жет быть оп­ре­де­ле­но как её про­ек­ции на фик­си­ро­ван­ные пря­мые, пе­ре­се­каю­щие­ся в од­ной точ­ке, на­зы­вае­мой на­ча­лом ко­ор­ди­нат. Эти про­ек­ции на­зы­ва­ют­ся ко­ор­ди­на­та­ми точ­ки, а пря­мые – ося­ми ко­ор­ди­нат.

Рис. 1.

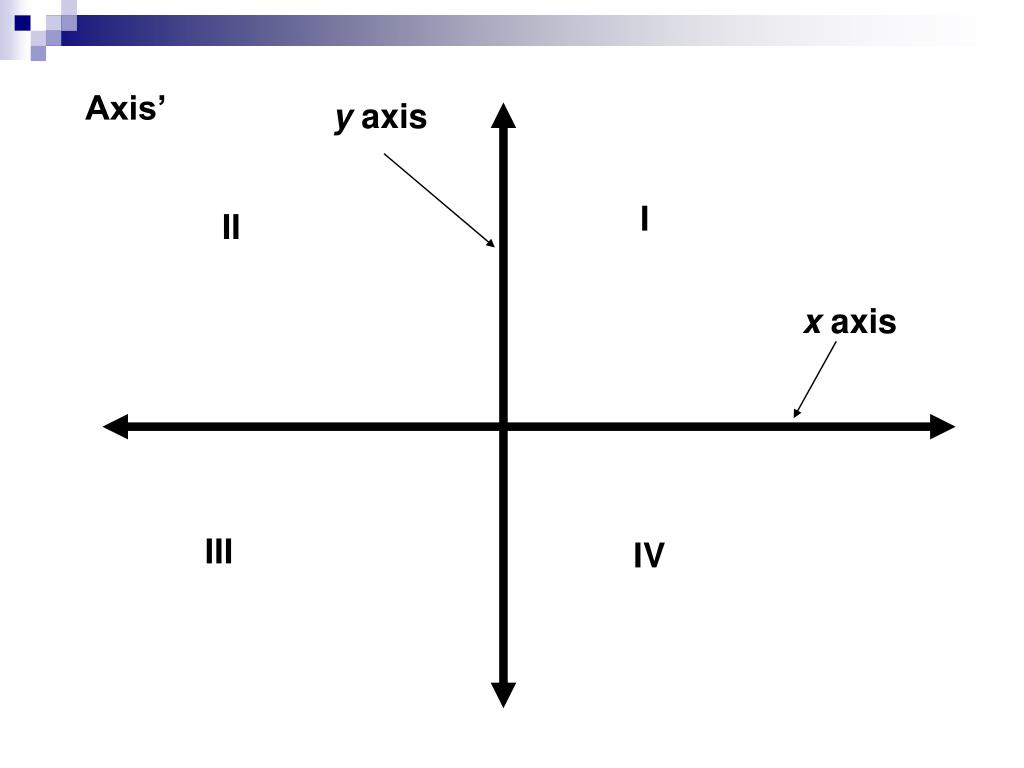
В об­щем слу­чае на плос­ко­сти Д. с. к. (аф­фин­ная сис­те­ма ко­ор­ди­нат) за­да­ёт­ся точ­кой $O$ (на­ча­лом ко­ор­ди­нат) и упо­ря­до­чен­ной па­рой при­ло­жен­ных к ней не ле­жа­щих на од­ной пря­мой век­то­ров $e_1$ и $e_2$ (ба­зис­ных век­то­ров). Пря­мые, про­хо­дя­щие че­рез на­ча­ло ко­ор­ди­нат в на­прав­ле­нии ба­зис­ных век­то­ров, на­зы­ва­ют ося­ми ко­ор­ди­нат дан­ной Д. с. к. Пер­вая, оп­ре­де­ляе­мая век­то­ром $e_1$, на­зы­ва­ет­ся осью абс­цисс (или осью $Ox$), вто­рая – осью ор­ди­нат (или осью $Oy$). Са­ма Д. с. к. обо­зна­ча­ет­ся $Oe_1e_2$ или $Oxy$. Де­кар­то­вы­ми ко­ор­ди­на­та­ми точ­ки $M$ (рис. 1) в Д. с. к. $Oe_1e_2$ на­зы­ва­ет­ся упо­ря­до­чен­ная па­ра чи­сел ($x$, $y$), ко­то­рые яв­ля­ют­ся ко­эф­фи­ци­ен­та­ми раз­ло­же­ния век­то­ра $\overrightarrow {OM}$ по ба­зи­су $\{e_1,e_2\}$, т. е. $x$ и $y$ та­ко­вы, что $\overrightarrow{OM}=xe_1+ye_2$. Чис­ло $x$, $- \infty \lt x \lt \infty$, на­зы­ва­ет­ся абс­цис­сой, чис­ло $y$, $- \infty \lt y \lt \infty$, – ор­ди­на­той точ­ки $M$. Ес­ли ($x$, $y$) – ко­ор­ди­на­ты точ­ки $M$, то пи­шут $M$($x$, $y$).

Ес­ли на плос­ко­сти вве­де­ны две Д. с. к. $Oe_1e_2$ и $O’e’_1e’_2$ так, что век­то­ры ба­зи­са $\{e’_1,e’_2\}$ вы­ра­же­ны че­рез век­то­ры ба­зи­са $\{e_1,e_2\}$ фор­му­ла­ми $$e’_1=a_{11}e_1+a_{12}e_2,\quad e’_2=a_{21}e_1+a_{22}e_2$$ и точ­ка $O’$ име­ет в Д. с. к. $Oe_1e_2$ ко­ор­дина­ты $(x_0,y_0)$, то ко­ор­ди­на­ты $(x,y)$ точ­ки $M$ в Д. с. к. $Oe_1e_2$ и ко­ор­ди­на­ты $(x’,y’)$ той же точ­ки в Д. с. к. $O’e’_1e’_2$ свя­за­ны со­от­но­ше­ния­ми $$x=a_{11}x’+a_{21}y’+x_0,\quad y=a_{12}x’+a_{22}y’+y_0.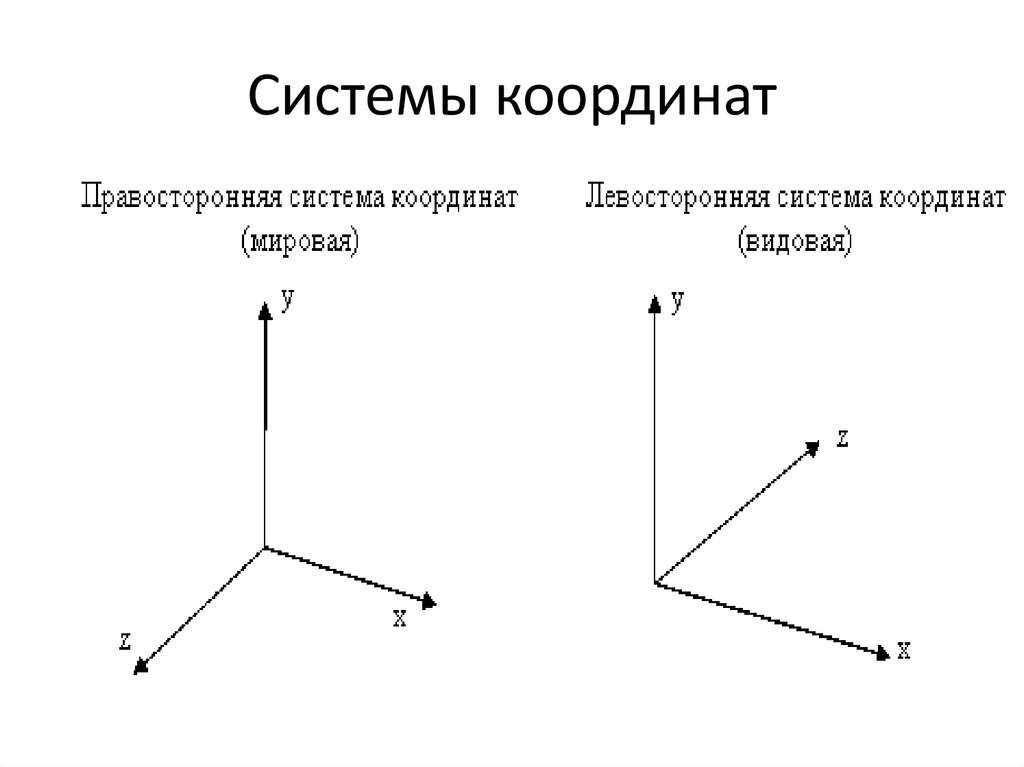 2}.$.

Фор­му­лы пе­ре­хо­да от од­ной пря­мо­уголь­ной Д. с. к. $Oxy$ к дру­гой пря­мо­уголь­ной Д. с. к. $O’x’y’$, на­ча­ло ко­то­рой $O’$ Д. с. к. $Oxy$ есть $O'(x_0,y_0)$, име­ют вид $$x=x’\cos \alpha-y’\sin \alpha+x_0,\quad y=x’\sin \alpha+y’\cos \alpha+y_0$$ или $$x=x’\cos \alpha+y’\sin \alpha+x_0,\quad y=x’\sin \alpha-y’\cos \alpha+y_0.$$

Рис. 2.

В пер­вом слу­чае сис­те­ма $O’x’y’$об­ра­зу­ет­ся по­во­ро­том ба­зис­ных век­то­ров $e_1$, $e_2$ на угол $\alpha$ и по­сле­дую­щим пе­ре­но­сом на­ча­ла ко­ор­ди­нат $O$ в точ­ку $O’$ (рис. 2), а во вто­ром слу­чае – по­во­ро­том ба­зис­ных век­то­ров $e_1$, $e_2$ на угол $\alpha$, по­сле­дую­щим от­ра­же­ни­ем оси, со­дер­жа­щей век­тор $e_2$ от­но­си­тель­но пря­мой, не­су­щей век­тор $e_1$, и пе­ре­но­сом на­ча­ла ко­ор­ди­нат $O$ в точ­ку $O’$ (рис. 3).

Рис. 3.

Ино­гда ис­поль­зу­ют­ся ко­со­уголь­ные Д. с. к., от­ли­чаю­щие­ся от пря­мо­уголь­ной тем, что угол ме­ж­ду еди­нич­ны­ми ба­зис­ны­ми век­то­ра­ми не яв­ля­ет­ся пря­мым.

Рис. 4.

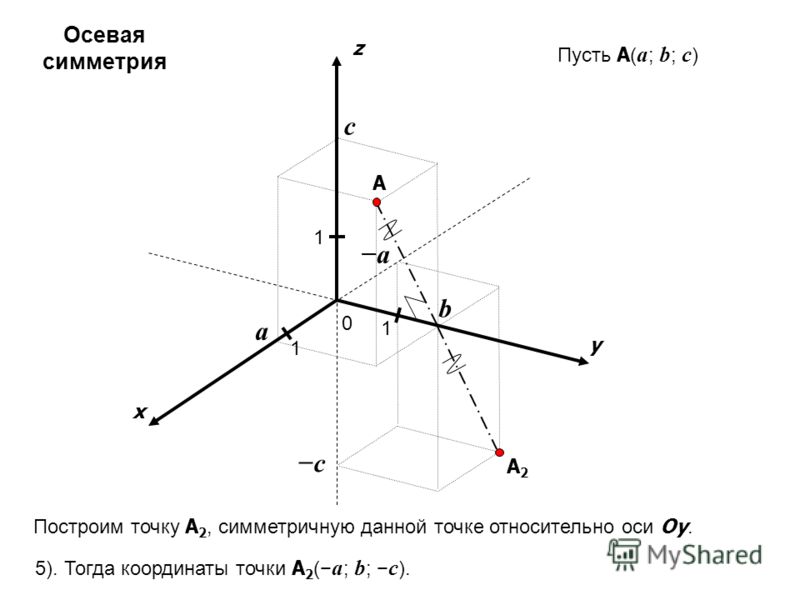
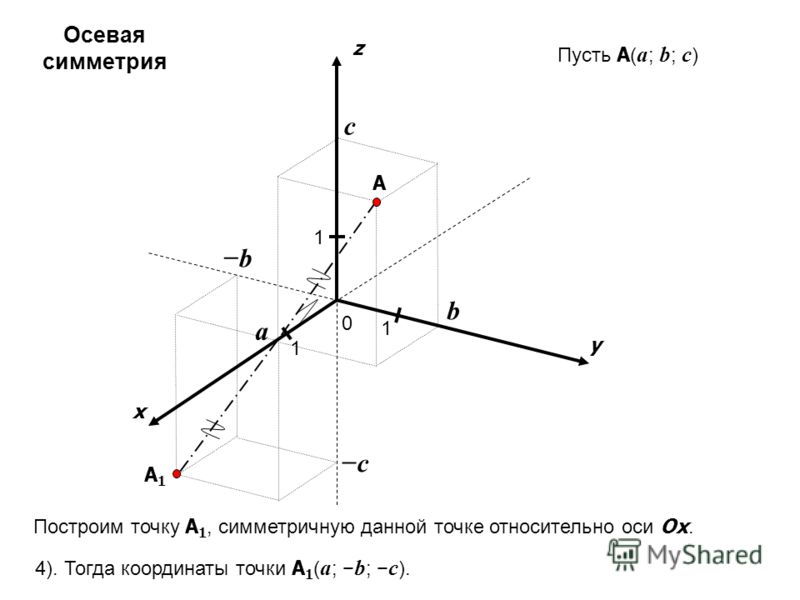
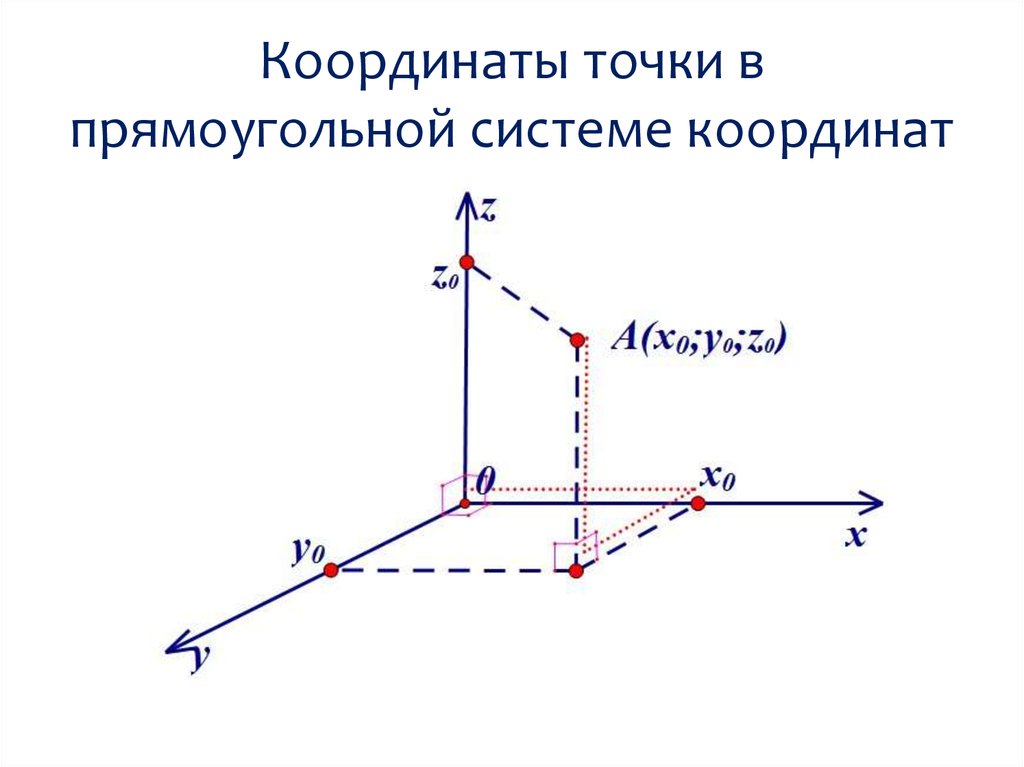
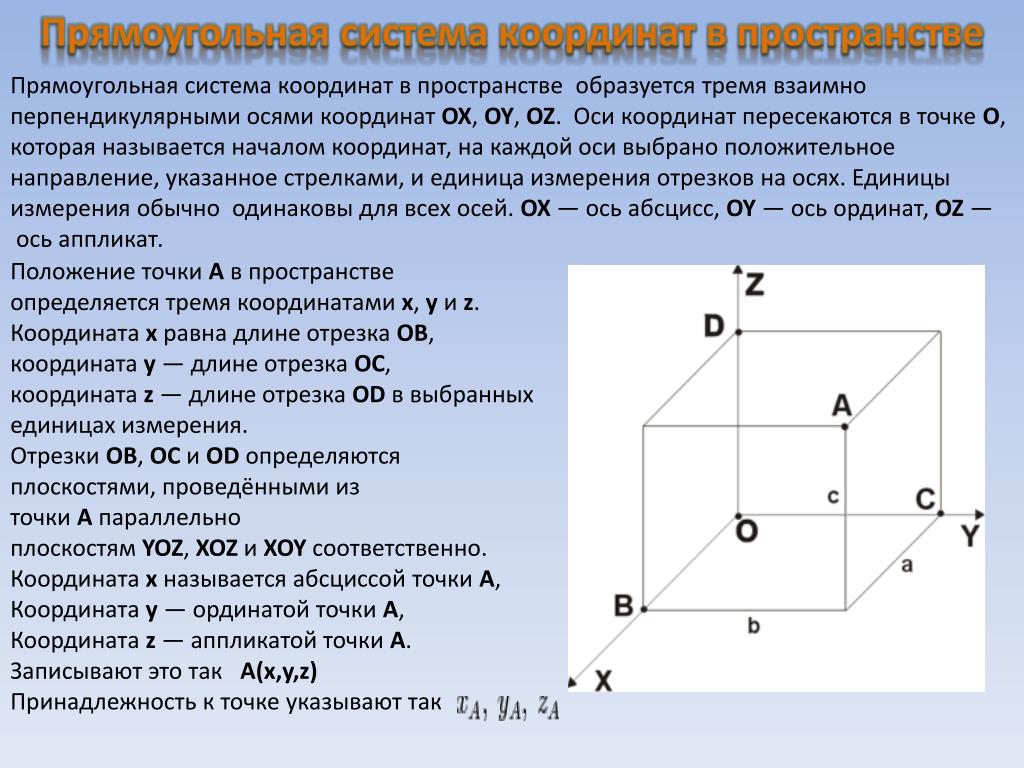
Ана­ло­гич­но оп­ре­де­ля­ет­ся об­щая Д. с. к. (аф­фин­ная сис­те­ма ко­ор­ди­нат) в про­стран­ст­ве: за­да­ёт­ся точ­ка $O$ – на­ча­ло ко­ор­ди­нат и упо­ря­до­чен­ная трой­ка при­ло­жен­ных к ней не ле­жа­щих в од­ной плос­ко­сти век­то­ров $e_1$, $e_2$, $e_3$ (ба­зис­ных век­то­ров). Как и в слу­чае плос­ко­сти, оп­ре­де­ля­ют­ся оси ко­ор­ди­нат – ось абс­цисс (ось $Ox$), ось ор­ди­нат (ось $Oy$) и ось ап­пли­кат (ось $Oz$) (рис. 4). Д. с. к. в про­стран­ст­ве обо­зна­ча­ет­ся $Oe_1e_2e_3$ (или $Oxyz$). Плос­ко­сти, про­хо­дя­щие че­рез па­ры осей ко­ор­ди­нат, на­зы­ва­ют­ся ко­ор­ди­нат­ны­ми плос­ко­стя­ми. Д. с. к. в про­стран­ст­ве на­зы­ва­ет­ся пра­вой, ес­ли по­во­рот от оси $Ox$ к оси $Oy$ со­вер­ша­ет­ся в на­прав­ле­нии, про­ти­во­по­лож­ном дви­же­нию ча­со­вой стрел­ки, ес­ли смот­реть на плос­кость $Oxy$ из к.-н. точ­ки по­ло­жи­тель­ной по­лу­оси $Oz$, в про­ти­во­по­лож­ном слу­чае Д. с. к. на­зы­ва­ет­ся ле­вой. Ес­ли ба­зис­ные век­то­ры $e_1$, $e_2$, $e_3$ име­ют дли­ны, рав­ные еди­ни­це, и по­пар­но пер­пен­ди­ку­ляр­ны, то Д.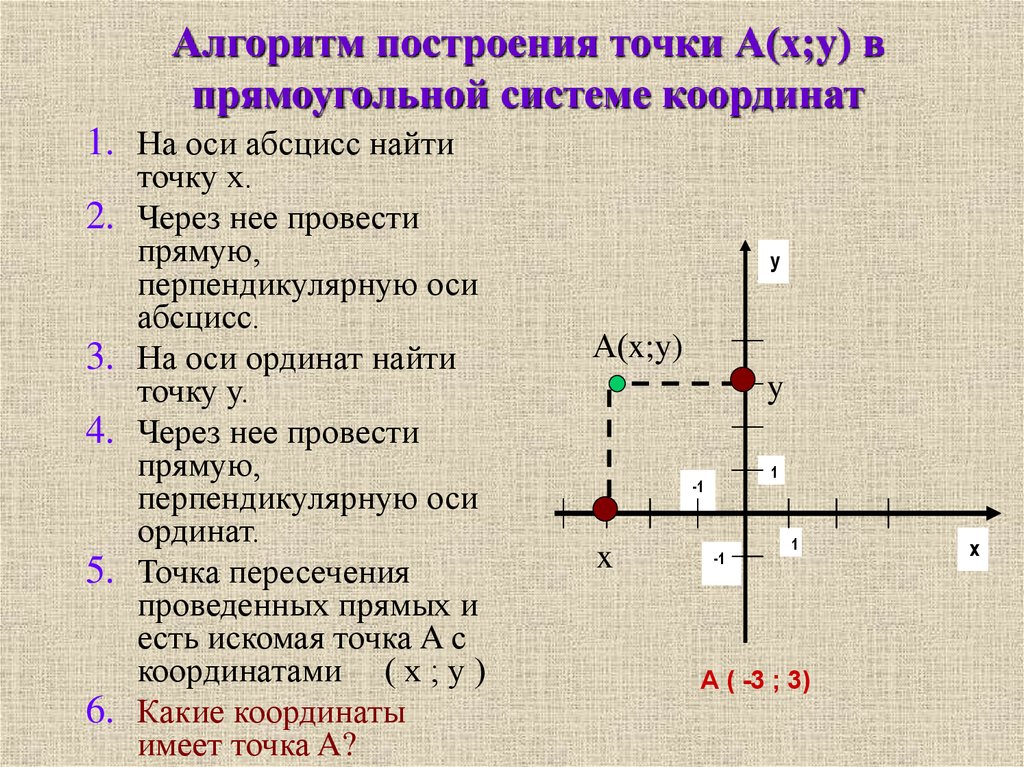  с. к. на­зы­ва­ет­ся пря­мо­уголь­ной. По­ло­же­ние од­ной пря­мо­уголь­ной Д. с. к. в про­стран­ст­ве от­но­ситель­но дру­гой пря­мо­уголь­ной Д. с. к. с той же ори­ен­та­ци­ей оп­ре­де­ля­ет­ся тре­мя эй­ле­ро­вы­ми уг­ла­ми.

Д. с. к. на­зва­на по име­ни Р. Де­кар­та, хо­тя в его соч. «Гео­мет­рия» (1637) рас­смат­ри­ва­лась ко­со­уголь­ная сис­те­ма ко­ор­ди­нат, в ко­то­рой ко­ор­ди­на­ты то­чек мог­ли быть толь­ко по­ло­жи­тель­ны­ми. В из­да­нии 1659–61 к «Гео­мет­рии» при­ло­же­на ра­бо­та голл. ма­те­ма­ти­ка И. Гуд­де, в ко­то­рой впер­вые до­пус­ка­ют­ся как по­ло­жи­тель­ные, так и от­ри­ца­тель­ные зна­че­ния ко­ор­ди­нат. Про­стран­ст­вен­ную Д. с. к. ввёл франц. ма­те­ма­тик Ф. Ла­ир (1679). В нач. 18 в. ус­та­но­ви­лись обо­зна­че­ния $x$, $y$, $z$ для де­кар­то­вых ко­ор­ди­нат.

Системы координат, проекции и преобразования—ArcGIS Pro

Данные, как правило, включают в себя массив чисел. Пространственные данные тоже, как правило, включают в себя массив чисел, но они также содержат в себе числовую информацию, которая позволяет вам расположить их где-то на поверхности Земли.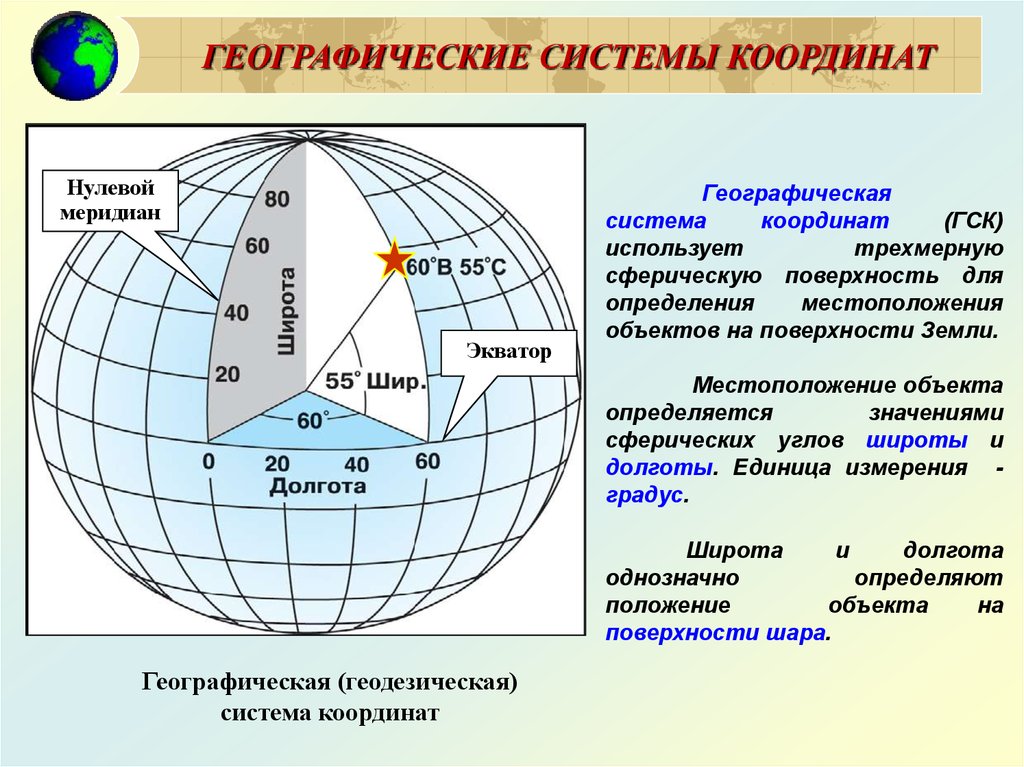 Эти числа являются частью системы координат, которая обеспечивает фрейм привязки для ваших данных, чтобы находить объекты на земле, чтобы сопоставлять ваши данные с другими данными, чтобы выполнять пространственный анализ с высокой точностью и чтобы делать карты.

Все пространственные данные создаются в каких-то системах координат независимо от того, идет ли речь о точках, линиях, полигонах, растрах или аннотациях. Сами координаты могут быть заданы различными способами – в десятичных градусах, футах, метрах или километрах; в действительности, в качестве системы координат может использоваться любая форма измерения. Определение этой системы измерений является первым шагом для выбора системы координат, которая будет отображать ваши данные в корректном положении в ArcGIS Pro относительно других ваших данных.

Системы координат

Данные заданы в горизонтальной и вертикальной системах координат. Горизонтальные системы координат отвечают за размещение объектов на поверхности Земли, а вертикальные определяют локализацию относительных высот и глубин объектов.

Существует три типа горизонтальных систем координат – географические, системы координат проекции и местные. Вы можете узнать, в какой системе координат находятся ваши данные, открыв свойства слоя. Единицами измерения географических систем координат являются, как правило, десятичные градусы, в которых выражаются значения долготы (координата x) и широты (координата y). Местоположение данных может быть выражено положительными и отрицательными числами: положительными значениями х и у для районов севернее экватора и восточнее начального меридиана и отрицательными значениями х и у для районов к югу от экватора и западнее начального меридиана.

Пространственные данные могут выражаться с помощью систем координат проекции. Для этих координат чаще используются линейные единицы измерения вместо угловых. Наконец, некоторые данные могут быть выражены в локальной системе координат с условным началом координат (0, 0 или другие значения) в произвольном местоположении, которое может находиться в любом месте земного шара.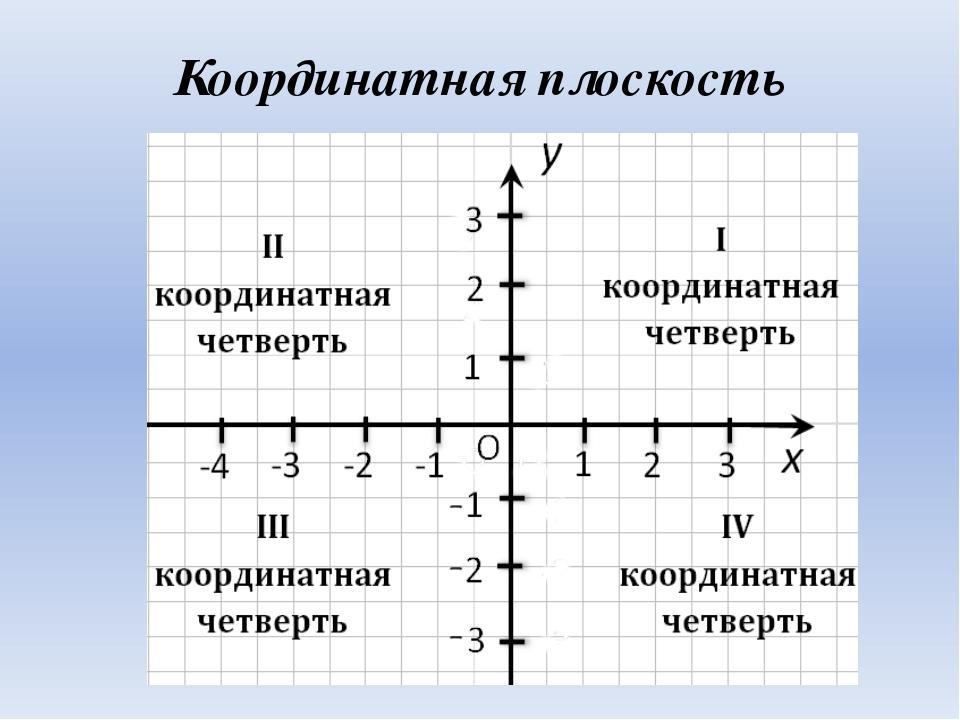 Местные системы координат часто используются для крупномасштабной картографии (небольшие участки земли). Условное начало координат может совпадать или не совпадать с известными реальными координатами, но для целей сбора данных для измерения направлений и расстояний скорее будет использоваться местная система координат, нежели глобальные координаты. В локальных системах координат в качестве единиц измерения обычно используются футы и метры.

В географической системе координат измерения выполняются в угловых единицах, тогда как в системе координат проекции – в линейных единицах.

Вертикальные системы координат бывают гравитационные и эллипсоидальные. В гравитационных вертикальных системах координат системой отсчета является средний уровень моря. Высоты в эллипсоидальных системах координат отсчитываются от полученной математическими методами поверхности сферы или эллипсоида.

Загрузитьсписок поддерживаемых географических и вертикальных систем координат.

Проекции

Проекция — это способ отображения системы координат и своих данных на плоской поверхности, т.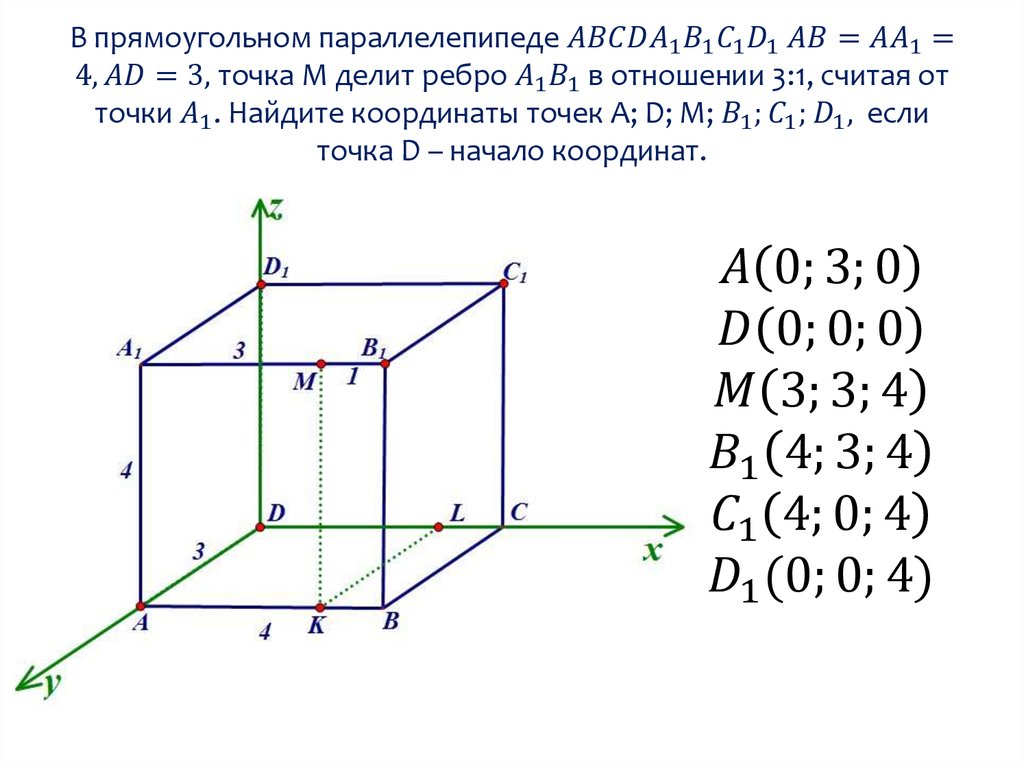 е. на листе бумаги или на экране. Для конвертации системы координат, используемой на не плоской поверхности Земли, в систему координат для плоской поверхности используются математические вычисления. Поскольку транспонировать не плоскую поверхность на плоскую без искажений невозможно, используются разные картографические проекции с разными свойствами. Некоторые сохраняют форму, другие – расстояние. Третьи сохраняют площадь или направление. Ваш выбор картографической проекции должен быть сформирован экстентом, местоположением и свойствами, которые вы захотите сохранить. На платформе ArcGIS существует более четырех тысяч систем координат, поэтому вы, вероятно, найдете подходящую для ваших данных. Если нет — вы можете создать пользовательскую систему координат для отображения данных.

ArcGIS Pro проецирует данные на лету, поэтому любые данные, которые вы добавите в карту, примут систему координат, заданную для первого добавленного слоя. При условии, если система координат первого добавленного слоя будет определяться корректно, все другие данные с корректной системой координат будут перепроецироваться на лету в систему координат карты. Такой подход облегчает исследование и отображение данных, но он не должен использоваться для проведения анализов или редактирования, поскольку это может привести к неточностям из-за несопоставленных между разными слоями данных. При проецировании на лету данные прорисовываются медленнее. Если вы собираетесь проводить анализы или редактировать данные, сначала спроецируйте их в соответствующую систему координат, доступную для всех ваших слоев. Так будет создана новая версия ваших данных.

Загрузитьсписок поддерживаемых систем координат проекции.

См. раздел поддерживаемых картографических проекций.

Преобразования

Даже после того, как система координат задана, вы все равно можете захотеть использовать данные в другой системе координат. В таких случаях может оказаться полезной преобразование. Преобразование конвертирует данные между разными географическими или вертикальными системами координат. Если ваши данные не будут согласованы, то при проведении любых картографических действий или анализа вы будете сталкиваться с трудностями и неточностями.

Загрузитьсписок поддерживаемых географических и вертикальных преобразований.

Связанные разделы

Отзыв по этому разделу?

Система координат в C как массив

Я не думаю, что вы можете сделать это с массивами, но вы можете сделать это с указателями на элементы массива.

Однако, я бы не стал этого делать, если бы у меня не было ОЧЕНЬ серьезной причины . Отрицательно индексируемые указатели не будут тем, что ожидает читатель вашего кода, поэтому их легко будет случайно использовать неправильно. Для ясности вам может быть лучше с функциональным решением, если только оно не должно быть ОЧЕНЬ быстрым.

С этим покончено, давайте сделаем это!

Судя по вашей попытке, вы можете запутаться в массивах и указателях. Помните, что это не одно и то же.

Теперь C не запрещает вам использовать отрицательные индексы, что может иметь смысл, когда вы используете указатель.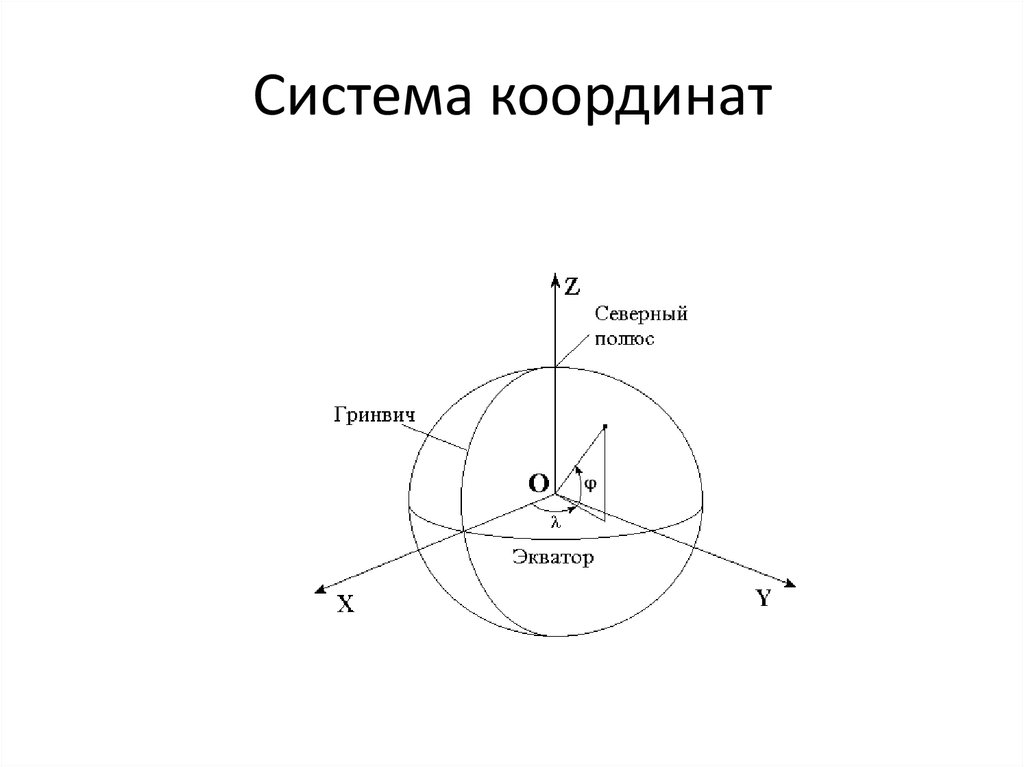 Итак, вы можете сделать это:

 int a[5];
 интервал *b = а + 2; // или &a[2]
 b[-2] // это [0]
 b[-1] // это [1]
 b[0] // ia a[2] и т. д.
 

Итак, я думаю, что следующий код вам подойдет.

 #define GRIDSIZE 101
.....
int map_memory[GRIDSIZE][GRIDSIZE];
int *map_rows[GRIDSIZE];
интервал **карта;
инт я;
int gridMidPoint = GRIDSIZE / 2;
for(i = 0; i < GRIDSIZE; i++) {
    map_rows[i] = &(map_memory[i][0]) + gridMidPoint;
}
карта = map_rows + gridMidPoint;
 

Затем вы можете использовать его именно так, как вы ожидаете - с размером сетки 101:

 for(i = -50; i <= 50; i++) {
    for(j = -50; j <= 50; j++) {
        карта[i][j] = i+j;
    }
}
 

Или, в более общем виде:

 for(i = -1 * gridMidPoint; i <= gridMidPoint; i++) {
    for(j = -1 * gridMidPoint; j <= gridMidPoint; j++) {
        карта[i][j] = i+j;
    }
}
 

Поскольку оба массива создаются в стеке, ничего освобождать не нужно.

Что здесь происходит? Позвольте мне сломать его.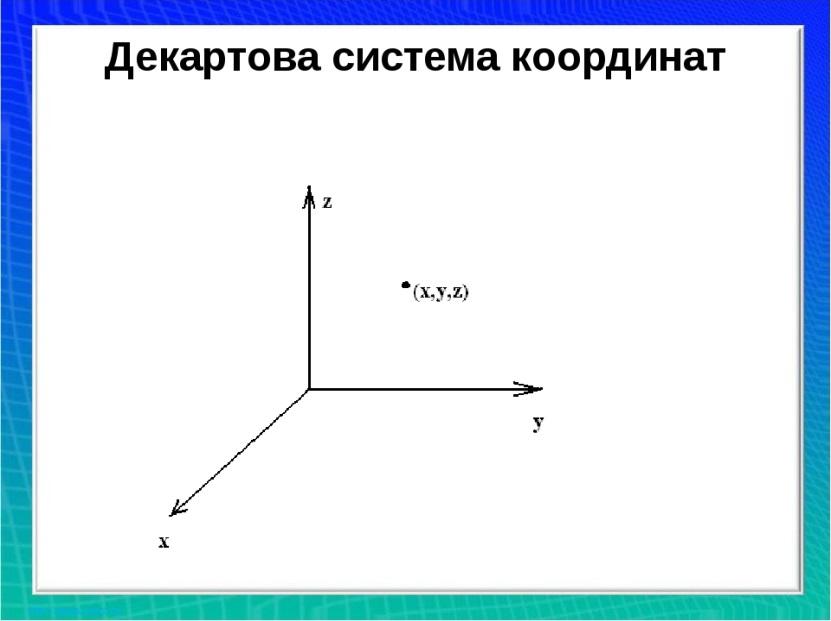 Сначала мы создаем резервный массив:

 int map_memory[GRIDSIZE][GRIDSIZE];
 

Далее нам нужен массив указателей, которые мы собираемся использовать в качестве строк:

 int *map_rows[GRIDSIZE];
 

Нам нужно, чтобы это были указатели, потому что они будут указывать на середину массивов в только что созданном двумерном массиве.

 int gridMidPoint = GRIDSIZE / 2;
 

Здесь мы вычисляем среднюю точку. Я предполагаю, что вам нужно одинаковое количество элементов массива по обе стороны от нуля, поэтому вам не нужен +1 из вашего примера.

 for(i = 0; i < GRIDSIZE; i++) {
    map_rows[i] = &(map_memory[i][0]) + gridMidPoint;
}
 

Этот код перебирает каждый элемент в нашем массиве строк и устанавливает эту строку так, чтобы она указывала на середину соответствующей строки в двумерном массиве. Вы также можете написать:

 map_rows[i] = &map_memory[i][gridMidPoint];
 

Но я лично считаю, что вариант с лишними скобками и дополнением читается понятнее.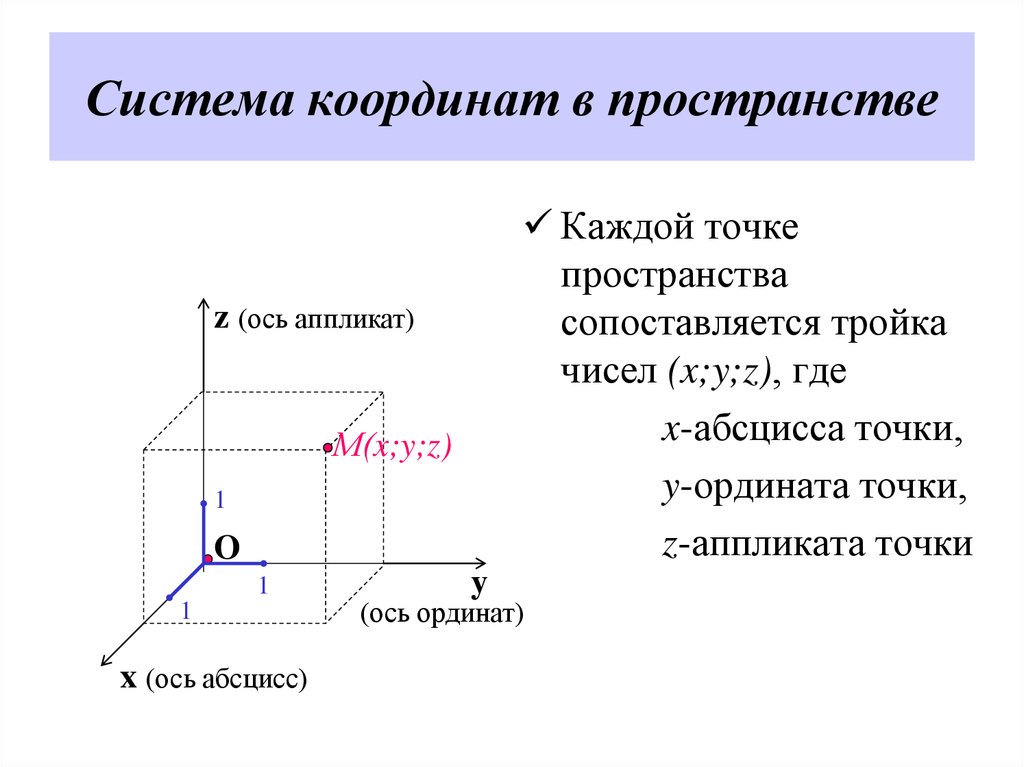 Я думаю, если вы делаете необычные вещи с указателями, вы должны точно объяснить, что происходит, для следующего человека, который прочитает ваш код.

Наконец, нам нужно, чтобы наш указатель map указывал на середину строк:

 map = map_rows + gridMidPoint;
 

Готово!

Помните, что двумерные массивы на самом деле являются одним блоком непрерывной памяти. Это означает, что map[0][gridMidPoint+1] совпадает с местоположением map[1][-1*gridMidPoint] . На самом деле это ничем не отличается от обычного двумерного массива, но об этом следует помнить при отладке.

Типы систем координат

Система координат — это метод представления точек в пространстве заданных размеров с помощью координат. Два типа системы координат, представляющие интерес для FIA, — это географическая система координат, основанная на координатах широты и долготы, и система координат проекта, представляющая проекцию географической системы координат на плоскость.

Самый простой способ добавить систему координат в проект HEC-FIA — импортировать шейп-файл проекции в окно карты. Координаты задаются на основе файла *.prj первой карты, добавленной в окно карты.

Другой способ добавить систему координат в проект HEC-FIA — в диалоговом окне Свойства карты по умолчанию для нажать View . Откроется диалоговое окно Информация о координатах карты .

Нажмите Загрузить из файла, и Открытие браузера Откроется, перейдите к файлу .prj, который содержит правильную проекцию для проекта HEC-FIA.

Несколько замечаний по производительности. Если используется файл фонового изображения или файл интернет-карты, лучше всего установить проекцию карты фонового изображения, это ускоряет масштабирование за счет повторного проецирования данных. на лету, а не фоновое изображение. Кроме того, фоновое изображение лучше при просмотре в исходной проекции.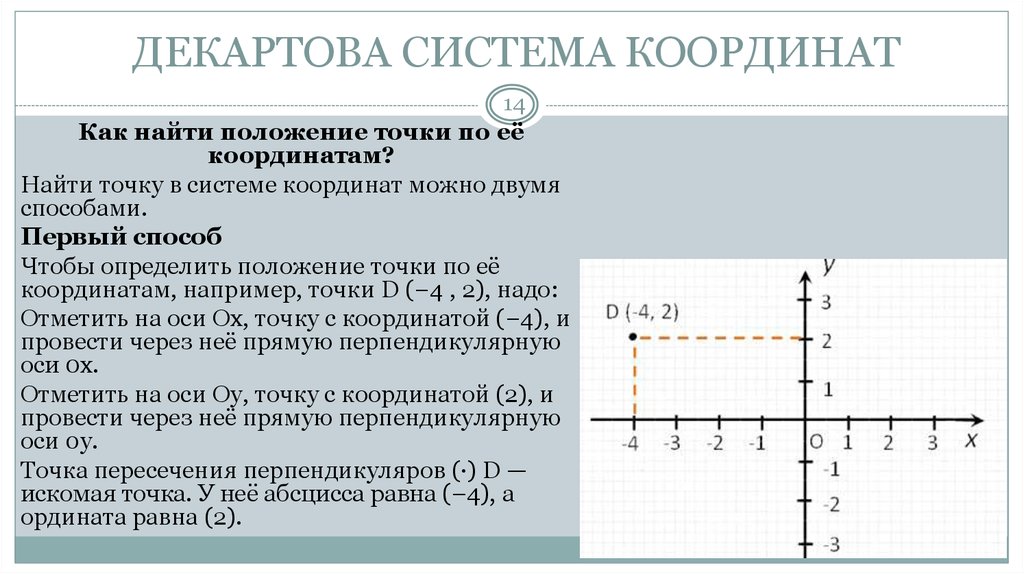
Системы координат, доступные в HEC-FIA, показаны в таблице C.1. В этой таблице также показаны единицы измерения и тип сфероида для каждой системы координат. Сфероид (эллипсоид) — это форма Земли, используемая в расчетах, которые преобразуют положения на искривленной поверхности Земли в положения на плоской карте. Это часть горизонтальной исходной точки, которая аппроксимирует искривленную поверхность земли над частью земного шара.

Таблица: Системы координат, доступные в HEC-FIA

0005

80131

Система координат X-Y также известна как Мировая система координат (WCS). Это накладывает сетку на объекты слоя, чтобы установить координаты x и y для каждой точки слоя. Исходная точка (0,0) может быть расположена где угодно, но каждый объект расположен относительно исходной точки. Система координат X-Y не имеет спецификации сфероида.

Для установки параметров системы координат X-Y:

1. В меню Карты выберите Свойства карты по умолчанию . Откроется диалоговое окно Свойства карты по умолчанию для .

2. В поле Coordinate System отображается имя выбранной системы координат (по умолчанию X-Y). Нажмите Посмотреть . Откроется диалоговое окно Информация о координатах карты .

3. Из списка System выберите X-Y .
4. Из шт. , выберите единицы измерения для системы координат X-Y.
5. Нажмите OK . Диалоговое окно Информация о координатах карты закроется. В поле Система координат диалогового окна Свойства карты по умолчанию для отображается X-Y .

Система координат Google/Bing Web Mercator представляет собой разновидность проекции Меркатора и является стандартом для большинства картографических веб-приложений. Также используется Bing и OpenStreet.

1. В меню Карты выберите Свойства карты по умолчанию . Откроется диалоговое окно Свойства карты по умолчанию для .

2. В поле Система координат отображается имя выбранной системы координат (по умолчанию X-Y). Нажмите Посмотреть . Откроется диалоговое окно Информация о координатах карты .
3. Из списка System выберите Google/Bing Web Mercator .
4. Информация о координатах карты В диалоговом окне отображается информация о системе координат.
5. Нажмите OK . Диалоговое окно Информация о координатах карты закроется. В поле Система координат диалогового окна Свойства карты по умолчанию для должно отображаться Google/Bing Web Mercator .

Каждая из различных систем координат имеет собственный набор параметров, редактируемых в Информация о координатах карты 9диалоговое окно 0004 (рисунок C.7). Для географической системы координат пользователи могут определить единицы и сфероид .

Чтобы задать параметры для Географической системы координат:

1. В меню Карты выберите Свойства карты по умолчанию . Откроется диалоговое окно Свойства карты по умолчанию для .
2. В поле Coordinate System отображается имя выбранной системы координат (по умолчанию X-Y). Нажмите Просмотр . Откроется диалоговое окно Информация о координатах карты .
3. Из списка System выберите Geographic .
4. Из списка Units выберите единицы для системы координат Geographic . Единственными доступными единицами измерения должны быть радиана, углового градуса и угловой секунды .
5. В списке Spheroid выберите тип сфероида для системы координат Geographic .
6. Нажмите OK . Диалоговое окно Информация о координатах карты закроется. В поле Система координат диалогового окна Свойства карты по умолчанию для должно отображаться Географическое .

Система координат Universal Transverse Mercator (UTM) является проекционной системой координат. UTM используется для определения горизонтальных положений во всем мире путем деления поверхности Земли на зоны по шесть градусов с центральным меридианом в центре каждой зоны.

Чтобы задать параметры универсальной поперечной системы координат Меркатора:

1. В меню Карты выберите Свойства карты по умолчанию . Откроется диалоговое окно Свойства карты по умолчанию для .

2. В поле Coordinate System отображается имя выбранной системы координат (по умолчанию X-Y). Нажмите Посмотреть . Откроется диалоговое окно Информация о координатах карты .

3. От Системный список , выберите Универсальный поперечный Меркатор .
4. Из списка Units выберите единицы измерения для системы координат Universal Transverse Mercator .
5. Из списка Spheroid выберите тип сфероида для системы координат Universal Transverse Mercator .
6. В поле Зона UTM введите номер зоны UTM.
7. Нажмите OK . Информация о координатах карты диалоговое окно закрывается. В поле Coordinate System диалогового окна Свойства карты по умолчанию для должно отображаться Universal Transverse Mercator .

Государственная система координат (SPCS) была создана в 1930-х годах и в настоящее время охватывает все пятьдесят штатов. Зоны были установлены для каждого состояния с использованием либо конформной проекции Ламберта, либо траверс-меркаторской проекции. Единицы обычно в футах (NAD27) или метрах (NAD83).

Для установки параметров системы координат государственной плоскости:

1. В меню Карты выберите Свойства карты по умолчанию . Откроется диалоговое окно Свойства карты по умолчанию для .

2. В поле Coordinate System отображается имя выбранной системы координат (по умолчанию X-Y). Нажмите Посмотреть . Откроется диалоговое окно Информация о координатах карты .

3. Из списка System выберите Плоские координаты штата .
4. В Зона поле, введите зону для состояния. Эти коды являются кодами FIPS.
5. Нажмите OK . Диалоговое окно Информация о координатах карты закроется. В поле Coordinate System диалогового окна Свойства карты по умолчанию для должны отображаться координаты State Plane .

Равновеликая коническая проекция Альберса была создана для картографирования больших площадей. Проекция является эквивалентной проекцией, где площади пропорциональны, а направления верны в ограниченных областях.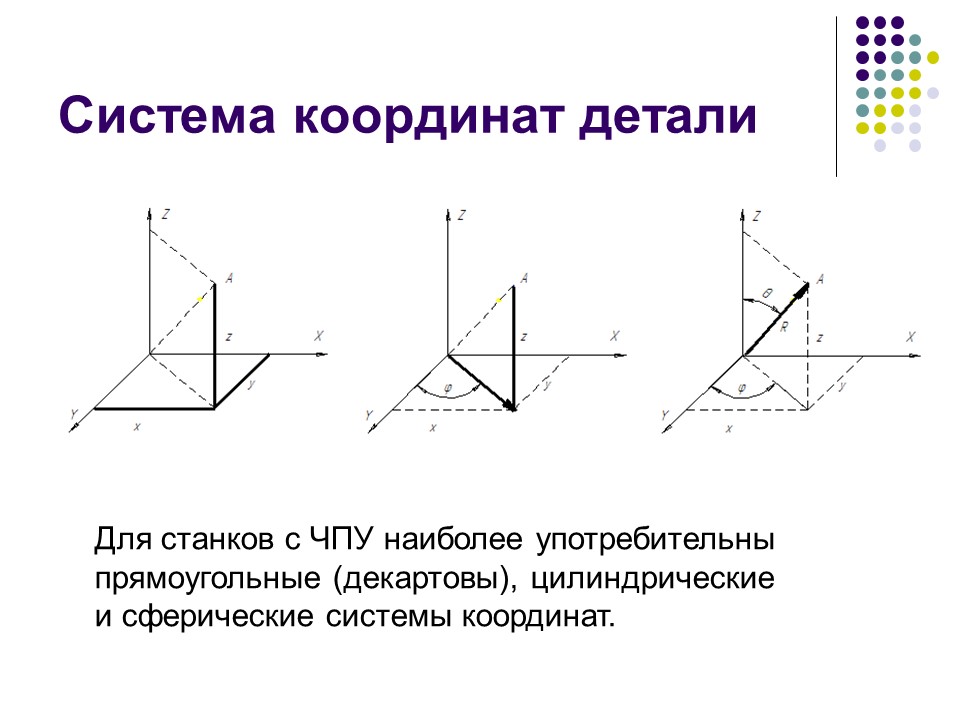

Чтобы задать параметры для равновеликой конической системы координат Альберса:

1. В меню Карты выберите Свойства карты по умолчанию . Откроется диалоговое окно Свойства карты по умолчанию для .
2. В поле Coordinate System отображается имя выбранной системы координат (по умолчанию X-Y). Нажмите Посмотреть . Откроется диалоговое окно Информация о координатах карты .

3. Из списка System выберите Альберс равновеликий конический .

4. В списке Units выберите единицы измерения для системы координат Albers Equal-Area Conic.
5. Из списка Spheroid (рис. C.10) выберите тип сфероида для системы координат Albers Equal-Area Conic.
6. Осталось ввести угловые параметры, необходимые для точной настройки проекции. При указании широты введите N или S , а для долготы введите E или W . Используйте ПРОБЕЛ для переключения между записями.
7. Нажмите OK . Диалоговое окно Информация о координатах карты закроется. В поле Coordinate System диалогового окна Свойства карты по умолчанию для должно отображаться Albers Equal-Area Conic .

Ламбертовская конформная коническая проекция широко используется для картографирования областей мира с преимущественной ориентацией восток-запад. Подобно равноконической проекции Альберса, однако проекция не выполняется на равной площади.

Чтобы задать параметры для конформно-конической системы координат Ламберта:

1. В меню Карты выберите Свойства карты по умолчанию . Откроется диалоговое окно Свойства карты по умолчанию для .

2. В поле Coordinate System отображается имя выбранной системы координат (по умолчанию X-Y). Нажмите Посмотреть . Откроется диалоговое окно Информация о координатах карты .

   3.От Системный список , выберите Конформная коническая Ламберта .
   4. Из списка Units выберите единицы для системы координат конформной конической формы Ламберта.
   5. Из списка Spheroid выберите тип сфероида для системы координат Lambert Conformal Conic.
   6. При указании широты введите N или S , а для долготы введите E или W . Используйте ПРОБЕЛ для переключения между записями.
   7. Нажмите OK . Диалоговое окно Информация о координатах карты закроется. В поле Система координат диалогового окна Свойства карты по умолчанию для должно отображаться Конформная коническая Ламберта .

В поперечной проекции Меркатора сфера проецируется на цилиндр, касающийся центрального меридиана. Он похож на проект Lambert Conformal Conic, но используется для изображения больших площадей с ориентацией север-юг. Многие национальные сетки основаны на поперечной проекции Меркатора.

Чтобы задать параметры поперечной системы координат Меркатора:

1. В меню Карты выберите Свойства карты по умолчанию . Откроется диалоговое окно Свойства карты по умолчанию для .

2. В поле Coordinate System отображается имя выбранной системы координат (по умолчанию X-Y). Нажмите Посмотреть . Откроется диалоговое окно Информация о координатах карты .

3. Из системы выберите Поперечное Меркатора .
4. В списке Единицы выберите единицы измерения поперечной системы координат Меркатора.
5. В списке Spheroid выберите тип сфероида для поперечной системы координат Меркатора.
6. Введите коэффициент масштабирования для центрального меридиана в поле Коэффициент масштабирования для центрального меридиана .
7. При указании широты введите N или S , а для долготы введите E или W . Используйте ПРОБЕЛ для переключения между записями.
8. Нажмите OK . Диалоговое окно Информация о координатах карты закроется. В поле Система координат диалогового окна Свойства карты по умолчанию для должно отображаться Поперечное Меркатора .

Стандартная гидрологическая сетка (SHG) представляет собой сетку карты с квадратными ячейками переменного разрешения, определенную для граничащих Соединенных Штатов, на основе системы конической проекции Albers Equal-Area.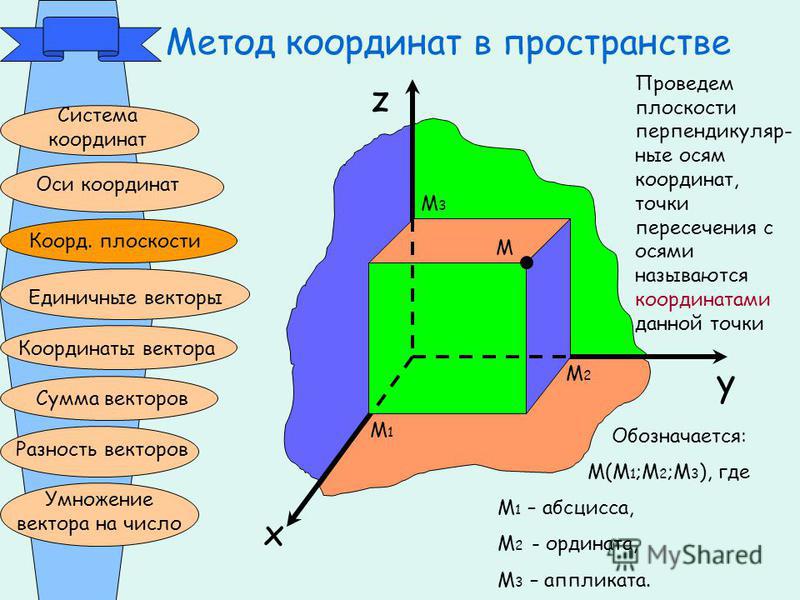 Параметры установлены в соответствии с координатами карты USACE для SHG.

Для просмотра параметров системы координат равновеликой конической системы Альберса (SHG) :

1. В меню Maps выберите Свойства карты по умолчанию . Откроется диалоговое окно Свойства карты по умолчанию для .

2. В поле Coordinate System отображается имя выбранной системы координат (по умолчанию X-Y). Нажмите Посмотреть . Откроется диалоговое окно Информация о координатах карты .

   3. Из списка System выберите Albers Equal-Area Conic (SHG) .
   4. Из списка Units выберите единицы измерения для системы координат Albers Equal-Area Conic (SHG).
   5. Из списка Spheroid выберите тип сфероида для системы координат Albers Equal-Area Conic (SHG).
   6.Остальные параметры носят информационный характер и не редактируются.
   7. Нажмите OK . Диалоговое окно Информация о координатах карты закроется. В Система координат в диалоговом окне Свойства карты по умолчанию для , Равновеликая коническая Альберса (SHG) должна отображаться.

Проекционная система Проекта гидрологического анализа осадков (HRAP) представляет собой разновидность полярной стереографической системы координат. Параметры установлены в соответствии с координатами карты NWS, используемыми для сетки радаров.

Для просмотра параметров полярной стереографической системы координат (HRAP):

1. Из Карты меню, нажмите Свойства карты по умолчанию . Откроется диалоговое окно Свойства карты по умолчанию для .
2. В поле Coordinate System отображается имя выбранной системы координат (по умолчанию X-Y). Нажмите Посмотреть .