Центратор это: Зачем нужны центраторы?
Содержание
Центратор звенный наружный ЦЗН
Звенный наружный центратор для труб применяются в основном в нефтепроводной строительной отрасли, а именно для центровки торцов труб (обечаек) при сварочных работах диаметром 20 мм по 2020 мм.
Наружный центратор для труб стоит взять на вооружение каждому сварщику, так как это удобное, простое и неприхотливое в работе приспособление для стяжки труб перед сваркой.
Мы производим центраторы по собственным разработанным техническим условиям ТУ 3663-001-42930233-2016.
Центраторы цзн
Маталлический наружный центратор для труб состоит из легированных стальных многозвенников марки 09Г2С, соединённых друг с другом опорными роликами рис.1. Опорные ролики на центраторе цзн мы также производим из той же легированной стали 09Г2С.
Наша компания производит центраторы звенные наружные ЦЗН по собственно разработанным техническим условиям ТУ 3663-001-42930233-2016.
Почему мы применяем именно эту сталь 09Г2С в производстве центраторов ЦЗН, ЦНЭ, ЦНГ:
- Обладает хорошей твердостью и прочностью.
- Хорошая стойкость к трещинам при стягивании трубы центратором.
- Повышенный предел выносливости.
- Низкая к деформации при зажиме трубопровода друг с другом.
Центратор для сварки
Применяется центратор для сварки труб, как в полевых условиях, при рабочей температуре от -600С до +600С, так и в условиях промышленных предприятий. В отличии от гидравлического центратора ЦНГ, центратор ЦЗН более транспортабельный и удобный в работе!
ВНИМАНИЕ ЗАКАЗЧИКА! Мы производим центраторы на любой диаметр трубы начиная от 20 мм до 2020 мм. По желанию заказчика наши специалисты готовы разработать и испытать любые размеры центраторов!
Рис 1
1,2,3-звено; 4-винт; 5-траверса; 6-пята; 7-рукоятка; 8-ролик; 9-ось.
- Пример заказа
- Центратор ЦЗН-530, где ЦЗН-центратор звенный наружный; 530-диаметр трубопровода.
|
Центратор |
Центраторы для труб |
Центратор наружный |
|
Центратор для сварки |
Центратор звенный наружный |
Центратор цзн |
|
Центраторы для труб |
Центраторы для труб |
Центраторы для труб |
Технические характеристики центраторов ЦЗН.
| Марка центратора | Диаметр центрируемых труб (мм) | Масса (кг) | Цена изделия руб с НДС |
| ЦЗН 25 | 25 | 1 | По запросу |
| ЦЗН 32 | 32 | 1,5 | По запросу |
| ЦЗН 45 | 45 | 2,5 | По запросу |
| ЦЗН 57 | 57 | 4 | По запросу |
| ЦЗН 76 | 76 | 4,7 | По запросу |
| ЦЗН 89 | 89 | 5 | По запросу |
| ЦЗН 108 | 108 | 6,5 | По запросу |
| ЦЗН 114 | 114 | 6,5 | По запросу |
| ЦЗН 159 | 159 | 10,4 | По запросу |
| ЦЗН 168 | 168 | 10,4 | По запросу |
| ЦЗН 219 | 219 | 8,1 | По запросу |
| ЦЗН 273 | 273 | 10 | По запросу |
| ЦЗН 325 | 325 | 10,5 | По запросу |
| ЦЗН 377 | 377 | 11,5 | По запросу |
| ЦЗН 426 | 426 | 15 | По запросу |
| ЦЗН 530 | 530 | 20 | По запросу |
| ЦЗН 630 | 630 | 32 | По запросу |
| ЦЗН 720 | 720 | 36 | По запросу |
| ЦЗН 820 | 820 | 39 | По запросу |
| ЦЗН 1020 | 1020 | 46 | По запросу |
| ЦЗН 1060 | 1060 | 50 | По запросу |
| ЦЗН 1220 | 1220 | 54 | По запросу |
| ЦЗН 1420 | 1420 | 61 | По запросу |
| ЦЗН 1620 | 1620 | 75 | По запросу |
| ЦЗН 1720 | 1720 | 80 | По запросу |
| ЦЗН 1820 | 1820 | 85 | По запросу |
| ЦЗН 2020 | 2020 | 95 | По запросу |
Центратор цена
Цена на центраторы звенные наружные ЦЗН вы можете узнать у наших специалистов. Зайдите в раздел контакты.
Зайдите в раздел контакты.
Комплектация поставки центратора.
- Центратор ЦЗН.
- Паспорт. «Инструкция по эксплуатации».
- Сертификат соответствия.
На каждом центраторе указывается диаметр изделия, номер партии, завод изготовитель ООО «РОСНЕФТЕГАЗКОМПЛЕКТ».
Наша компания также производит и другие типы центраторов.
- Центратор наружный эксцентриковый ЦНЭ.
- Центратор звенный наружный титановый ЦЗНТ.
- Центратор наружный гидравлический ЦНГ.
- Центратор звенный наружный гидрофицированный ЦЗН-Г.
- Центратор звенный наружный уневерсальный ЦЗН-У.
- Подогреватель стыков труб ПСТ.
- Термозащитные пояса ТП и ТЗП.
Центратор для труб в «СтальПром»
Что объединяет буровые скважины, канализационные системы, промышленные и технологические магистрали? В них используются трубы большого диаметра и протяжённости.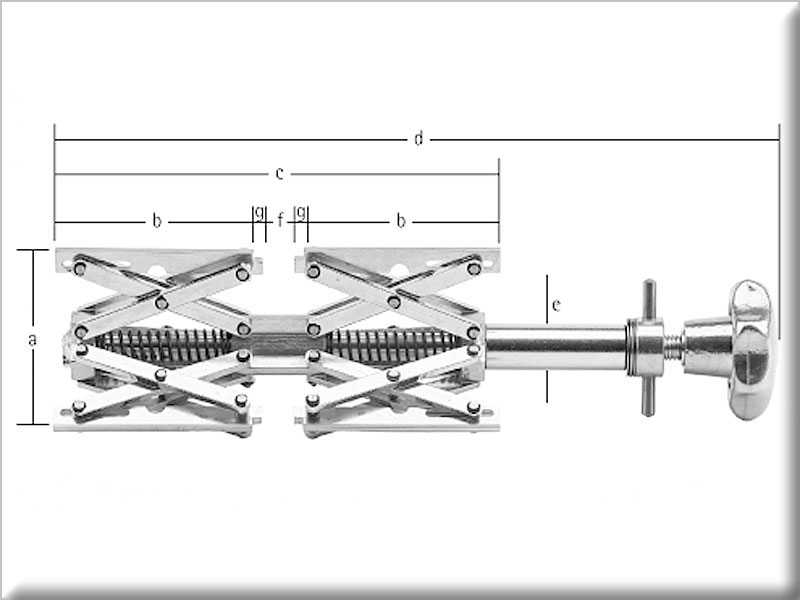 Чтобы ровно состыковать отдельные участки трубопровода, используется центратор для труб — специальное фиксирующее устройство.
Чтобы ровно состыковать отдельные участки трубопровода, используется центратор для труб — специальное фиксирующее устройство.
Конструктивно центратор представляет собой захват или распорку, удерживающие трубу снаружи или изнутри. Наружные трубные центраторы охватывают трубу по внешней стенке, подобно захватам. Удобнее тисков или универсальных зажимов. Не только фиксируют трубы в заданном положении, но и выпрямляют замятия и некоторые другие дефекты.
Виды наружных центраторов:
- Центратор звеньевой состоит из пластин, соединённых пальцевыми шарнирами. Стягивается винтовым механизмом или гидроприводом. Подходит для труб диаметром до 2000 мм. Мало весит, удобно и быстро монтируется на трубу.
- Центратор арочный состоит из двух клемм с откидными частями. Затяжка выполняется вручную или гидроприводом. Подходит для труб диаметром до 900 мм.
- Центратор цепной используется на трубах с наружным диаметром до 1400 мм. Состоит из цепи и струбцин с регулировочными болтами.
 Стягивается вручную. Подходит как для прокладки новых, так и для ремонта действующих трубопроводов, удобен в полевых условиях. Часто цепные центраторы комплектуются ключом для регулировки болтов.
Стягивается вручную. Подходит как для прокладки новых, так и для ремонта действующих трубопроводов, удобен в полевых условиях. Часто цепные центраторы комплектуются ключом для регулировки болтов. - Центратор эксцентриковый. Конструктивно схож с арочным, но затягивается эксцентриковым зажимом. Приспособление ускоряет работу, но сравнительно быстро изнашивается. Применяется на трубах диаметром до 500–600 мм.
- Струбцинный центратор для труб малого диаметра используется в быту для ремонта канализационных и водопроводных систем.
Для затягивания наружных центраторов всех типов используют дополнительное оборудование и инструменты: ключи, гидроприводы и пр.
Внутренний центратор для труб
Внутренний центратор трубный, как следует из названия, устанавливается внутри трубы и работает как распорка. Широко применяется в трубах с полимерным покрытием, сварка которых ведётся изнутри. Отличается более сложной конструкцией по сравнению с внешними. Применяется на поворотных и неповоротных стыках.
Применяется на поворотных и неповоротных стыках.
Внутренние центраторы для сварки труб могут иметь ручной привод, но чаще работают на гидравлическом. Насос может быть ручным или автоматическим.
Преимущества внутренних центраторов:
- открытый сварочный стык, что обеспечивает непрерывность сварки и лёгкий контроль шва по всему диаметру;
- не только фиксируют трубы, но и устраняют овальность торцов;
- не дают трубам провисать.
Как работают внутренние центраторы для труб:
- устройство вводят с торца трубы, подлежащей сварке;
- создают необходимое усилие прижима;
- можно приступать к сварке;
- по окончании работ центратор удаляется с нового торца трубопровода при помощи штанг.
В коммунальном хозяйстве, при ремонте водных и газовых коммуникаций используются внутренние центраторы для сварки труб, поскольку вести работы снаружи мешают полимерное покрытие и утеплитель. Сварка таких труб также производится только изнутри.
Сварка таких труб также производится только изнутри.
Центраторы для сварки труб — выгодное приобретение
Использование трубных центраторов упрощает процесс сварки и значительно улучшает её качество. При правильном подборе устройств исключаются такие нарушения, как:
- несовпадение диаметров;
- провисание труб;
- овальность торцов.
При этом важно учитывать, что стоимость работ с применением центраторов для труб может существенно вырасти. Это касается в первую очередь трубопроводов большого диаметра (от 400 мм). Во-первых, трубы таких диаметров нужно фиксировать с обеих сторон, то есть приобретать два трубных центратора вместо одного. Во-вторых, вес промышленных моделей пружинных центраторов измеряется центнерами, поэтому их транспортировка и установка возможны только с использованием грузоподъёмных устройств. Эти расходы также следует заложить в бюджет.
При этом в целом затраты на использование наружных центраторов для труб окупаются безупречным качеством сварки, что увеличивает срок службы трубопровода, уменьшает вероятность утечек и других проблем.
В компании «СтальПром» широкий выбор устройств для труб разных диаметров и видов. При необходимости поможем подобрать центратор трубный наружный или внутренний, который оптимально подойдёт для решения ваших задач.
Централизатор
в nLab
Пропустить навигационные ссылки |
Домашняя страница |
Все страницы |
Последние версии |
Обсудить эту страницу |
Содержание
Контекст
Теория групп
Теория групп
- группа, ∞-группа
- групповой объект, групповой объект в (∞,1)-категории
- абелева группа, спектр
- суперабелева группа
- групповое действие, ∞-действие
- представление, ∞-представление
- прогруппа
- однородное пространство
Классические группы
общая линейная группа
унитарная группа
- специальная унитарная группа. проективная унитарная группа
ортогональная группа
- специальная ортогональная группа
симплектическая группа
Конечные группы
конечная группа
симметричная группа, циклическая группа, группа кос
классификация конечных простых групп
спорадические конечные простые группы
- Группа монстров, группа Матье
Групповые схемы
- алгебраическая группа
- абелева разновидность
Топологические группы
топологическая группа
компактная топологическая группа, локально компактная топологическая группа
максимальная компактная подгруппа
группа строк
Группы Ли
Группа Ли
компактная группа Ли
Группа Кац-Муди
Группы супер-Ли
супер группа Ли
суперевклидова группа
Высшие группы
2 группы
- модуль перекрестный, строгий 2-группный
н-группа
∞-группа
симплициальная группа
скрещенный комплекс
k-тупый групповой n-группоид
спектр
круг n-группа, струна 2-группа, пятигранник Ли 6-группа
Когомологии и расширения
групповых когомологий
- Групповое расширение
,
∞-группа расширения, Ext-группа
- квантовая группа
Изменить эту боковую панель
- Определение
- Свойства
- Связанные концепции
- Ссылки
Определение
Определение
Для данной группы GG и подмножества S⊂GS \,\subset\, G ее базового множества централизаторов подгруппа (также: коммутант ) группы SS в GG есть подгруппа
CG(S)≔{g∈G|∀s∈S(g⋅s=s⋅g)}⊂G
C_G (С)
\;\coloneqq\;
\большой\{
г \в г
\,\верт\,
\underset{s \in S}{\forall}
(
г \cdot s \,=\, s \cdot g
)
\большой\}
\;\подмножество\;
грамм
всех элементов c∈Gc \in G, коммутирующих с элементами SS.
Обратите внимание на сходство, но различие с концепцией подгруппы нормализаторов , см. Prop.
Свойства
Предложение
Для данного подмножества S⊂GS \подмножества G группы GG подгруппа централизаторов группы SS (Def.) является подгруппой подгруппы нормализаторов:
CG(S)⊂NG(S).
C_G (С)
\;
\подмножество
\;
N_G(С)
\,.
Доказательство
Поскольку элемент g∈Gg \in G, фиксирующий каждый элемент s∈Ss \in S по отдельности, уже фиксирует все подмножество как таковое:
∀s∈S(g⋅s=s⋅g)⇒( г⋅S=S⋅г).
\underset{s \in S}{\forall}
\большой(
г \cточка с
знак равно
с \cdot г
\большой)
\;\;\;\;\;
\Правая стрелка
\;\;\;\;\;
\большой(
г \cdot S
знак равно
S \cточка г
\большой)
\,.
Proposition
(централизаторы в T1T_1-группах закрыты)
Если GG является T1T_1-топологической группой, то все ее централизаторы являются замкнутыми подгруппами. {-1}
{-1}
\,.
}
(присоединенное действие GG на себя).
Заметив здесь, что:
это непрерывная функция по аксиомам топологической группы;
{s}⊂G\{s\} \subset G является замкнутым подмножеством в силу предположения, что GG является T1T_1-пространством (по этому предложению)
следует, что CG({s})⊂GC_G(\{s\}) \subset G является непрерывным прообразом замкнутого подмножества и, следовательно, само замкнуто (по этому предлож.).
Теперь для общего множества SS его централизатор, очевидно, является пересечением централизаторов (наборов одиночки) его элементов:
CG(S)=∩s∈SCG({s}).
C_G (С)
знак равно
\занижено{
с \в с
}{\колпачок}
C_G\большой(\{s\}\большой)
\,.
Поскольку каждый из факторов справа замкнут, согласно предыдущему аргументу подгруппа общего централизатора является пересечением замкнутых подмножеств и, следовательно, сама является замкнутым подмножеством.
стабилизатор подгруппа
подгруппа нормализатора
Ссылки
См. также
также
- Википедия, Центратор и нормализатор
Последняя редакция: 4 сентября 2021 г., 18:05:43.
См. историю этой страницы для получения списка всех вкладов в нее.
РедактироватьОбсудитьПредыдущая редакцияИзменения по сравнению с предыдущей редакциейИстория (9 ревизий)
Цитировать
Распечатать
Источник
централизаторов в алгебре
1 Абстрактные определения и свойства
Определение 1.
Пусть S — множество с бинарной операцией*. Пусть T — подмножество S. Тогда определим
центратор в S of T как подмножество
| CS(T)={s∈S:s*t=t*s, для всех t∈T}. |
Центр S определяется как CS(S). Это обычно обозначается как Z(S), где Z происходит от немецкого слова central . Подмножества и элементы центра
называются центральный .
Если мы рассмотрим *:S×S→S в действиях, мы можем описать левый
действие s*t и правильное действие t*s. Таким образом, централизатор представляет собой множество элементов
Таким образом, централизатор представляет собой множество элементов
для которого левое регулярное действие и правое регулярное действие совпадают, когда
к т.
Обычно возможно, чтобы s*t не лежало в T для s∈CS(T) и
t∈T, и также возможно, что если s,s′∈CS(T), то s*s′≠s′*s.
Поэтому не следует предполагать, что централизатор является центральным.
С дальнейшими аксиомами действия мы можем вывести некоторые естественные
для множества CS(T).
Предложение 2.
- 1.
Если A⊆B, то CS(B)⊆CS(A). В частности, CS(∅)=S.
- 2.
Если S имеет тождество, то CS(T) непусто. В частности, в этом случае Z(S) непусто. 1 1 Тождество S — это такой элемент e∈S, что e*s=s*e для всех s∈S.
- 3.
Если S ассоциативна и s,s′∈CS(T), то s*s′∈CS(T),
тогда мы говорим, что CS(T) закрыта для бинарной операции S. - 4.
Если s∈CS(T) и s имеет (сильную) инверсию-1, то
s-1∈CS(T). 2 2 Мы говорим, что инверсия является сильной, если s-1*(s*t)=t=(t*s)*s-1 для
все t∈S. Если операция ассоциативная, то это дается бесплатно. Там
Если операция ассоциативная, то это дается бесплатно. Там
являются естественными неассоциативными операциями с этим свойством, такими как альтернативные алгебры. - 5.
Если S коммутативно, то CS(T)=S.
- 6.
Если T является подмножеством центра S, то CS(T)=S.
Обратите внимание, что CS(T) может быть подмножеством, закрытым для операции без
предположение об ассоциативности, как, например, когда S коммутативен.
2 центратора в группах
В категории групп централизатор в группе G подмножества H можно переопределить как:
| CG(H)={g∈G:g-1hg=h, для всех h∈H}. |
Если рассматривать спряжение как групповое действие hg:=g-1hg, то отсюда следует, что
централизатор — это то же самое, что и точечный стабилизатор в G группы H, где действие
G на себя сопряжением. Из-за этого совпадения в некоторых контекстах
централизаторов применяется к точечному стабилизатору множества, на котором действует группа,
хотя этот контекст больше не относится к действию спряжения. Этот
Этот
особенно распространен, когда необходимо различать точечный стабилизатор
и установочный стабилизатор.
В этой категории централизатор всегда является подгруппой группы G. Кроме того, если H — нормальная
подгруппа группы G, то и CG(H).
3 Централизаторы в кольцах и алгебрах
Ибо мы рассматриваем кольца как алгебры над ℤ и сейчас говорим только о
алгебр, которые будут включать неассоциативные примеры.
В алгебре A на самом деле есть две бинарные операции над множеством A в
вопрос. Таким образом, абстрактное определение централизатора неоднозначно. Тем не менее, добавка
операция колец и алгебр всегда коммутативна, поэтому любой централизатор относительно этой
операция есть множество A. Таким образом, общепринято считать, что централизаторы
в этом контексте всегда ссылайтесь на мультипликативную операцию. Таким образом, мы имеем следующее
характеристики.
Предложение 3.
Для данной алгебры A над коммутативным кольцом R с единицей и подмножеством B кольца A, тогда
- 1.

CA(B) является подмодулем A.
- 2.
Если A ассоциативна, то CA(B) является подалгеброй.
- 3.
Z(A)≤CA(B), в частности, если A имеет 1, то 1∈CA(B) и, следовательно,
R встраивается в CA(B).
Замечания.
- •
Централизатор в алгебре также называется коммутантом. Эта терминология в основном используется в алгебрах операторов функционального анализа.
- •
Пусть R — кольцо (или алгебра). Для каждой упорядоченной пары (a,b) элементов R мы можем определить аддитивного коммутатора (a,b) как элемент ab-ba, записанный [a,b]. При этом можно альтернативно определить централизатор множества S⊆R в кольце R как
CR(S):={r∈R∣[r,s]=0 для всех s∈S}. Конечно, в этом определении нужны две операции (умножение и вычитание) вместо одной. Но приятный аспект этого определения заключается в том, что можно «измерить» коммутативность кольца с помощью аддитивной операции коммутации.
 Например, можно показать, что в теловом кольце, если каждый элемент аддитивно коммутирует с каждым аддитивным коммутатором, то кольцо должно быть полем.
Например, можно показать, что в теловом кольце, если каждый элемент аддитивно коммутирует с каждым аддитивным коммутатором, то кольцо должно быть полем.
4 централизатора в алгебрах Ли
Предположим, что 𝔤 — алгебра Ли над коммутативным кольцом характеристики, отличной от 2.
Учитывая подмножество T из 𝔤, тогда [s,t]=-[t,s] для s∈𝔤 и t∈T из аксиом
умножения алгебры Ли. Следовательно, всякий раз, когда [s,t]=[t,s], следует, что
-[t,s]=[t,s], так что [t,s]=0. Это мотивирует более распространенное переопределение
централизатор в алгебре Ли:
| C𝔤(T)={s∈𝔤:[s,t]=0, для всех t∈T}. |
Несмотря на несоответствие в характеристике 2, это новое определение заменяет исходное
определение централизаторов для алгебр Ли. Централизатор алгебры Ли является подалгеброй.
Если умножение Ли рассматривается как коммутатор, то [a,b]=ab-ba, например
это универсальная обертывающая алгебра, тогда 0=[a,b]=ab-ba совпадает с ab=ba, и поэтому
централизатор алгебры Ли совпадает с централизатором ассоциативной
конверт.
5 Централизаторы в других неассоциативных алгебрах
Централизатор не обязательно должен быть подалгеброй из-за отсутствия ассоциативности.
Однако есть примеры неассоциативных алгебр, где централизатор
тем не менее подалгебра, например, алгебры Ли, как показано выше. В травиальной моде, если
алгебра коммутативна, тогда CA(B)=A и, следовательно, централизатор является подалгеброй
но без всяких полезных свойств. Имеется подходящее дополнительное ограничение
добавить к централизаторам, чтобы заставить их быть подалгебрами и нести с собой
более полезен в коммутативной, но неассоциативной установке.
Мы пишем [a,b] для ab-ba, называемого коммутатором в A для a,b∈A, а также пишем
/a,b,c/ для (ab)c-a(bc) и назовем его ассоциатором в A для a,b,c∈A. 3 3 Это обозначение
для ассоциаторов нестандартен, но стандарт [a,b,c]=(ab)c-a(bc), вероятно, сбивает с толку, учитывая
обычная запись коммутатора уже используется. Тогда мы
можно переопределить централизатор в A подмножества T множества A как



Всего комментариев: 0